图形学初步----------多边形填充算法
参考博文:
https://blog.csdn.net/xiaowei_cqu/article/details/7693985
https://blog.csdn.net/xiaowei_cqu/article/details/7712451
https://blog.csdn.net/wodownload2/article/details/52154207
https://blog.csdn.net/u013044116/article/details/49737585/
https://blog.csdn.net/guanyuqiu/article/details/53010025
一、概述
一般来讲,计算机的填充轮廓线的方法有两大类:扫描转换和种子填充。
扫描转换:按扫描线的顺序确定某一点是否位于多边形或轮廓形范围之内。这些算法一般从多边形或轮廓线的“顶部”开始进行到“底部”。扫描转换技术适用于光栅扫描设备和画线显示器。在画线显示器中用于画剖面线或轮廓的阴影线。如下
种子填充:首先假定封闭轮廓线内某点是已知的。然后算法开始搜索与种子相邻且位于轮廓线内的点。如果相邻点不位于轮廓线内,那么就已经到达轮廓线的边界。如果相邻点位于轮廓线内,那么这个点就成为新的种子点,然后继续递归地搜索下去,种子填充算法只适用于光栅扫描设备。
二、多边形填充
多边形
多边形在计算机中有顶点表示和点阵表示两种。
顶点表示就是用多边形的顶点序列来表示多边形。点阵表示是用位于多边形内的象素集合来表示多边形。顶点表示占内存少,几何意义强,易于进行几何变换;而点阵表示丢失了许多几何信息(如边界、顶点)。但光栅显示图形需要点阵表示形式。
多边形的扫描转换就是把多边形的顶点表示转换为点阵表示。
多边形扫描转换
填充多边形最简单的方法就是:
检查光栅的每一像素是否位于多边形内。但是这种效率实在太低了。有人曾经想到要用包围盒来减少计算量,所谓包围盒就是包含该多边形的最小矩形。只有在包围盒的那些点需要检查。但是这个算法如果遇到下右图也不见得是种好方法。
于是有人提出了多边形的扫描转换,在给定的扫描线上,像素这种特性只在多边形的边和该扫描线交点处才会发生变化。于是我们就可以拿这些交点来操作,通过一系列算法进行填充,比如下图:
我们可以看到,扫描线2和多边形交于x=1和x=8,这两个交点把扫描线分成了三段:
x<1 多边形外
1<=x<=8 多边形内
x>8 多边形外我们只需要把1<=x<=8,y=2,这段像素置成填充的值,而x<1,y=2;x>8,y=2这段像素置成背景色就可以了。以此类推,只要是能求出交点,让计算机把交点认识清楚,就能够准确无误的完成填充。那么怎么“认识”交点呢?
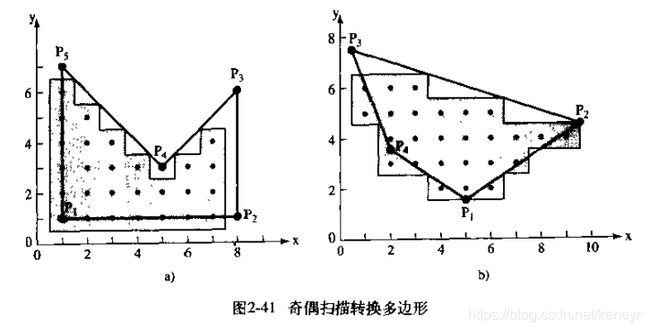
关于这个方法,有人提出了简单的奇偶扫描转换算法,它的主要思路就是:在扫描线开始时,奇偶位设置为0,表示扫描线在多边形的外部;扫描线与多边形第一次相交时,奇偶位设置为1,表示扫描线现在在多边形的内部;到下一个交点时,奇偶位设置为0,表示扫描线已通过多边形,又在多边形的外部。当奇偶位为0时,像素设置成多边形背景色,否则,设置为多边形色。
后来有人提出了更为有效的有序边表算法,它的基本思想是将多边形边与扫描线的交点进行排序。这个算法是本文的重点,最后会用代码实现。
1,首先来说下这个算法用到的数据结构:边表NET+活性边表AET。原理上讲,填充的时候是根据活性边表AET进行填充的,但是活性边表AET的更新又是依据边表NET。那么NET到底存储的是什么呢,用“边”的思路理解有点别扭,在我看来这个NET存储的就是多边形顶点与扫描线相交的信息:
数据结构:
x 当前扫描线与边的交点坐标;dx从当前扫描线到下一条扫描线间x的增量((x2-x1)/(y2-y1));ymax 该边所交的最高扫描线
数据结构代码表示:
/*定义结构体用于活性边表AET和新边表NET*/
typedef struct XET
{
double x;
double dx, ymax;
XET* next;
}AET,NET;举例:
对于下图多边形:
它的边表NET就是:
我们看到扫描线1,它与P2(5,1)相交对吧~, 那么x的值就是5,由于经过P2的边有两条,而这两条边y的最大值分别是2,3;斜率的倒数分别是-3,2.5。于是边表NET头结点1后面跟的两个节点就这样写了
为什么扫描线4的边表为空呢,因为扫描线4与多边形相交的边p1p6,p3p4已经被记录了,不再是新边了,所以不记录了。如果还是看不懂的话,看这个blog,讲的一看就懂:
https://blog.csdn.net/wodownload2/article/details/52154207
边表根据多边形进行初始化的代码如下:
/*初始化头结点*/
NET *pNET[1024];
for (i = 0; i <= MaxY; i++){
pNET[i] = new NET;
pNET[i]->dx = 0;
pNET[i]->x = 0;
pNET[i]->ymax = 0;
pNET[i]->next = NULL;
}/*扫描并建立NET表*/
for (i = MinY; i <= MaxY; i++){
/*i表示扫描线,扫描线从多边形的最底端开始,向上扫描*/
for (int j = 0; j < vertNum;j++)
/*如果多边形的该顶点与扫描线相交,判断该点为顶点的两条直线是否在扫描线上方
*如果在上方,就记录在边表中,并且是头插法记录,结点并没有按照x值进行排序,毕竟在更新AET的时候还要重新排一次
*所以NET表可以暂时不排序
*/
if (ThePolygon.m_Vertex[j].y == i){
/*笔画前面的那个点*/
if (ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].y > ThePolygon.m_Vertex[j].y){
NET *p = new NET;
p->x = ThePolygon.m_Vertex[j].x;
p->ymax = ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].y;
p->dx = double((ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].x - ThePolygon.m_Vertex[j].x)) / double((ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].y - ThePolygon.m_Vertex[j].y));
p->next = pNET[i]->next;
pNET[i]->next = p;
}
/*笔画后面的那个点*/
if (ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].y > ThePolygon.m_Vertex[j].y){
NET *p = new NET;
p->x = ThePolygon.m_Vertex[j].x;
p->ymax = ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].y;
p->dx = double((ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].x - ThePolygon.m_Vertex[j].x)) / double((ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].y - ThePolygon.m_Vertex[j].y));
p->next = pNET[i]->next;
pNET[i]->next = p;
}
}
}然后就是动态的更新活性边表AET了, 更新的原则就是:
1、根据给出的多边形顶点坐标,建立NET表;
求出顶点坐标中最大y值ymax和最小y值ymin。
2、初始化AET表指针,使它为空。
3、执行下列步骤直至NET和AET都为空.
3.1、如NET中的第y类非空,则将其中的所有边取出并插入AET中;
3.2、如果有新边插入AET,则对AET中各边排序;
3.3、对AET中的边两两配对,(1和2为一对,3和4为一对,…),
将每对边中x坐标按规则取整,获得有效的填充区段,再填充.
3.4、将当前扫描线纵坐标y值递值1;
3.5、如果AET表中某记录的ymax=yj,则删除该记录 (因为每条边被看作下闭上开的);
3.6、对AET中剩下的每一条边的x递增dx,即x' = x+ dx .
想要看到具体动态的步骤还是参考这篇博文,给的太详细了,看完肯定能知道是怎么个流程:
https://blog.csdn.net/wodownload2/article/details/52154207
更新AET的代码如下:
/*建立并更新活性边表AET*/
for (i = MinY; i <= MaxY; i++){
/*更新活性边表AET,计算扫描线与边的新的交点x,此时y值没有达到临界值的话*/
NET *p = pAET->next;
while (p){
p->x = p->x + p->dx;
p = p->next;
}
/*更新完以后,对活性边表AET按照x值从小到大排序*/
AET *tq = pAET;
p = pAET->next;
tq->next = NULL;
while (p){
while (tq->next&&p->x >= tq->next->x)
tq = tq->next;
NET *s = p->next;
p->next = tq->next;
tq->next = p;
p = s;
tq = pAET;
}
/*从AET表中删除ymax==i的结点*/
AET *q = pAET;
p = q->next;
while (p){
if (p->ymax == i){
q->next = p->next;
delete p;
p = q->next;
}
else{
q = q->next;
p = q->next;
}
}
/*将NET中的新点加入AET,并用插入法按X值递增排序*/
p = pNET[i]->next;
q = pAET;
while (p){
while (q->next&&p->x >= q->next->x)
q = q->next;
NET *s = p->next;
p->next = q->next;
q->next = p;
p = s;
q = pAET;
}
/*配对填充颜色*/
p = pAET->next;
while (p&&p->next){
for (float j = p->x; j <= p->next->x; j++){
pDC->SetPixel(static_cast(j), i,fillCol);
}
p = p->next->next;
}
} 所以整个函数的实现是这样的:
void CCGPainterView::ScanlineConvertion(CDC *pDC, MyPolygon ThePolygon, COLORREF fillCol)
{
//Write your own scan-line convertion algorithm here.
/*定义结构体用于活性边表AET和新边表NET*/
typedef struct XET
{
double x;
double dx, ymax;
XET* next;
}AET,NET;
//CPoint *ThePolygon.m_Vertex;
int vertNum = ThePolygon.m_VerticeNumber;
/*计算最高点y的坐标,扫描线扫到y的最高点就结束*/
int MaxY = ThePolygon.m_Vertex[0].y;
int MinY = ThePolygon.m_Vertex[0].y;
int i;
for (i = 1; i < vertNum; i++){
if (ThePolygon.m_Vertex[i].y>MaxY)
MaxY = ThePolygon.m_Vertex[i].y;
if (MinY > ThePolygon.m_Vertex[i].y)
MinY = ThePolygon.m_Vertex[i].y;
}
/*初始化AET表,这是一个有头结点的链表*/
AET *pAET = new AET;
pAET->next = NULL;
/*初始化NET表,这也是一个有头结点的链表,头结点的dx,x,ymax都初始化为0*/
NET *pNET[1024];
for (i = 0; i <= MaxY; i++){
pNET[i] = new NET;
pNET[i]->dx = 0;
pNET[i]->x = 0;
pNET[i]->ymax = 0;
pNET[i]->next = NULL;
}
/*扫描并建立NET表*/
for (i = MinY; i <= MaxY; i++){
/*i表示扫描线,扫描线从多边形的最底端开始,向上扫描*/
for (int j = 0; j < vertNum;j++)
/*如果多边形的该顶点与扫描线相交,判断该点为顶点的两条直线是否在扫描线上方
*如果在上方,就记录在边表中,并且是头插法记录,结点并没有按照x值进行排序,毕竟在更新AET的时候还要重新排一次
*所以NET表可以暂时不排序
*/
if (ThePolygon.m_Vertex[j].y == i){
/*笔画前面的那个点*/
if (ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].y > ThePolygon.m_Vertex[j].y){
NET *p = new NET;
p->x = ThePolygon.m_Vertex[j].x;
p->ymax = ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].y;
p->dx = double((ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].x - ThePolygon.m_Vertex[j].x)) / double((ThePolygon.m_Vertex[(j - 1 + vertNum) % vertNum].y - ThePolygon.m_Vertex[j].y));
p->next = pNET[i]->next;
pNET[i]->next = p;
}
/*笔画后面的那个点*/
if (ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].y > ThePolygon.m_Vertex[j].y){
NET *p = new NET;
p->x = ThePolygon.m_Vertex[j].x;
p->ymax = ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].y;
p->dx = double((ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].x - ThePolygon.m_Vertex[j].x)) / double((ThePolygon.m_Vertex[(j + 1 + vertNum) % vertNum].y - ThePolygon.m_Vertex[j].y));
p->next = pNET[i]->next;
pNET[i]->next = p;
}
}
}
/*建立并更新活性边表AET*/
for (i = MinY; i <= MaxY; i++){
/*更新活性边表AET,计算扫描线与边的新的交点x,此时y值没有达到临界值的话*/
NET *p = pAET->next;
while (p){
p->x = p->x + p->dx;
p = p->next;
}
/*更新完以后,对活性边表AET按照x值从小到大排序*/
AET *tq = pAET;
p = pAET->next;
tq->next = NULL;
while (p){
while (tq->next&&p->x >= tq->next->x)
tq = tq->next;
NET *s = p->next;
p->next = tq->next;
tq->next = p;
p = s;
tq = pAET;
}
/*从AET表中删除ymax==i的结点*/
AET *q = pAET;
p = q->next;
while (p){
if (p->ymax == i){
q->next = p->next;
delete p;
p = q->next;
}
else{
q = q->next;
p = q->next;
}
}
/*将NET中的新点加入AET,并用插入法按X值递增排序*/
p = pNET[i]->next;
q = pAET;
while (p){
while (q->next&&p->x >= q->next->x)
q = q->next;
NET *s = p->next;
p->next = q->next;
q->next = p;
p = s;
q = pAET;
}
/*配对填充颜色*/
p = pAET->next;
while (p&&p->next){
for (float j = p->x; j <= p->next->x; j++){
pDC->SetPixel(static_cast(j), i,fillCol);
}
p = p->next->next;
}
}
} 我是在vs2013下,MFC框架下执行,最后的执行效果如下,填充速度还是非常快的:
本文主要是给出能运行的代码,关于原理更为详尽的解释请看参考blog。