C++最长上升子序列

最长上升子序列简介

题目描述
现有数列a1，a2，a3……aN。在其中找到严格递增序列ai1，ai2，ai3，……aiK（1 <= i1 < i2 < i3 < …… < iK <= N），请找出序列a的最长上升子序列的长度，既K的最大值。

输入格式
第一行：一个整数N。
第二行：N个整数a1，a2，a3……aN。

输出格式
一行，最大的K。

输入样例

10
5 10 8 9 7 10 13 12 25 13

输出样例

6

二维动态规划解法

提到DP，就一定就要去想：状态、转移方程、初值和答案了。

1. 状态：dp[i]指在1~i这i个数中，必须包含a[i]这个数的最长上升子序列。
2. 转移方程：if(a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1)（1 <= j <= i - 1）
   其实这个的意思就是：如果说在1~(i - 1)这(i - 1)个数中，a[j] < a[i]，a[i]就可以接上a[j]，形成一个比dp[j]又多了1的递增序列，因此每次判断并取最大值就行了。
3. 初值：dp[i] = 1（一个数本身就是一个递增序列）。
4. 答案：max{dp[i]}

（PS：NR指序列长度的上限）

# include 
# include  
# include 
# include 
# include 

using namespace std;

# define FOR(i, a, b) for(int i = a; i <= b; i++)
# define _FOR(i, a, b) for(int i = a; i >= b; i--)

const int NR = 100000;

int n, ans;
int a[NR + 2], dp[NR + 2];

int main()
{
     
    scanf("%d", &n);
    FOR(i, 1, n) scanf("%d", &a[i]);
    FOR(i, 1, n) dp[i] = 1;
    FOR(i, 2, n){
     
        FOR(j, 1, i - 1)
            if(a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1);
        ans = max(ans, dp[i]);
    }
    printf("%d\n", ans);
    return 0;
}

贪心二分查找解法

二维动态规划的时间复杂度为On^2，太多了，我们想去优化，可是我们发现直接在二维上改好像改不了，没办法，只好再想一个新的方法了。

这次，我们开一个新的数组f，f[i]表示当上升子序列长度为i时，此子序列最后一个元素的最小值。我们会发现这个f数组是随着i值的增加，f[i]不断增大的单调队列。因为如果长度为i的上升子序列最后一位都为f[i]了，那长度(i + 1)的最后一位至少也得是f[i] + 1了吧。

这样我们从1到n一个元素一个元素的分析，当到了第i个元素时，我们在f数组中找第一个大于等于a[i]的f[k]，这就代表长度为(k - 1)的上升子序列最后一位的最少值是f数组中最后一个小于a[i]的数，所以就让我们就可以把a[i]放到长度为(k - 1)的这个上升子序列的后面，形成一个新的长度为k的这个上升子序列，接下来更新f[k]的值f[k] = min(f[k], a[i])可我们发现我们找f[k]时就说了f[k]是f数组中第一个大于等于a[i]的数，所以直接f[k] = a[i]就好了。

下图仅供参考。

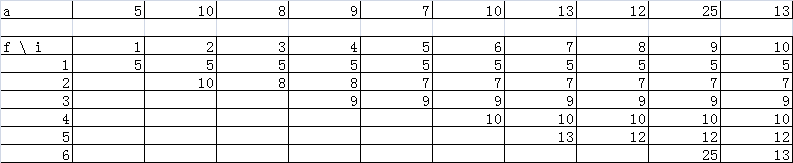
其中，在f数组中找第一个大于等于a[i]的f[k]时,可以用到二分查找函数中的lower_bound函数。

如果你还没有学过lower_bound可以到此网站学习lower_bound函数的用法
https://blog.csdn.net/SkeletonKing233/article/details/99479707

这样时间复杂度就从On^2降到了Onlogn，大大减少了时间的消耗。

以下为代码：

# include 
# include  
# include 
# include 
# include 

using namespace std;

# define FOR(i, a, b) for(int i = a; i <= b; i++)
# define _FOR(i, a, b) for(int i = a; i >= b; i--)

const int NR = 100000;

int n, ans;
int a[NR + 2];
int f[NR + 2];

int main()
{
     
	scanf("%d", &n);
 	FOR(i, 1, n) scanf("%d", &a[i]);
 	f[0] = -2e9;
 	FOR(i, 1, n){
     
 		int k = lower_bound(f, f + ans + 1, a[i]) - f;
 		f[k] = a[i];
 		ans = max(ans, k);
	}
	printf("%d\n", ans);
	return 0;
}

最长下降、不上升、不下降子序列

剩下的这三种都与第一种十分相像：

• 最长不下降子序列：就是把FOR循环中的lower_bound函数改成upper_bound函数。
• 最长下降子序列：就是把FOR循环前的f[0] = -2e9改成f[0] = 2e9之后再在全局写一个比较函数cmp，并在lower_bound函数中做为第4个参数引用
• 最长不上升子序列：就是先改成最长下降子序列，之后再把FOR循环中的lower_bound函数改成upper_bound函数。

PS：cmp函数的写法：

bool cmp(int x, int y){
     
	return x > y;
}