利用突触智能实现连续学习|从原理到代码解析（人生好难呀！）

利用突触智能实现连续学习|从原理到代码解析

问：读完这篇博客能学到什么？
答：1）掌握利用历史训练的累积梯度信息来缓解人工神经网络（深度学习）灾难性遗忘问题；2）能够自己在keras框架下写自己新提出的损失函数对应的优化器。

我在上一篇博客神经网络之灾难性遗忘问题中尝试对深度学习灾难性遗忘问题的研究进行综术。方法何其多，又怎么能综述的完全呢。但是那篇博客里已经给出解决深度学习灾难性遗忘问题的统一思想：利用历史信息来唤醒（抑制）那些对于历史知识来说比较重要的神经元参数（变化）。这篇博客将详细介绍一篇在前一篇综述里未提及的论文[1]，论文的作者认为历史训练过程中的梯度与参数调整量包含了权值相对历史知识的重要程度，也即可以利用历史梯度与参数调整量信息来度量各权值的重要程度，以此为依据来抑制重要权值的调整，从而达到避免历史知识被覆盖、缓解灾难性遗忘的目的。 网上可查，[1]存在两种论文题目《Improved multitask learning through synaptic intelligence》与《Continual Learning Through Synaptic Intelligence》。可能作者经过思考，将后者作为发表ICML2017的最终论文题目。哈哈！作者也有科研人员的普遍都有的小虚荣。明明Multitask Learning比Continual Learning更切论文核心方法的主题，但还是由于Continual Learning更加博人眼球，被强行上位。这只是小吐嘈啦，经受住ICML检视的论文，内部亮点还是很足的！下面我们从思想、方法、算法（公式）、程序四方面来解析这篇论文。Here we go！

1. 什么是突触智能(Synaptic Intelligence)

1.1 智能的定义

即然作者将他的方法上升到一种智能，那我们需要先知道什么是智能。才好去评价作者的工作。

[韦氏大辞典] Intelligence：The ability to learn or understand things or to deal with new or difficult situations.

中国古代思想家则把智与能看做是两个相对独立的概念，智能是智力与能力的总称。前者是智能的基础，也即知识，后者是指获取和运用知识求解的能力。

还是很虚…

为了让智能的概念更加具体，我们需要厘清智能、数据、信息、知识四者的关系。

数据=事实的记录。例如：如机器当前的运行速度、航向角、障碍的距离与速度等、环境三维点云；
信息=数据+意义。例如：障碍物正向自己靠近、远离、地面凹凸不平；
知识=解决问题的方案与策略。例如：前面有障碍物，则转向旁边或停下来，需要凹凸不平的地面，则减慢行驶速度。

智能就是具备从数据到发现、总结以及运用知识的能力。

论文中，作者从数据（历史训练过程中的梯度与参数调整量）中发现、总结知识（各权值的重要性），并运用（用来缓解灾难性遗忘问题）。从普通的数据总结出一种更新权值的策略，并用来缓解深度学习的灾难性问题。综上，论文的方法被称之为一种智能是合理的！可以负责任的说，这种智能对应人类一种高级的智能：学会如何学习（Learn to learn）。

1.2 从生物学而来的突触智能

作者认为人工神经网络（ANN）与生物神经网络之间最大的差异在于突触连接的复杂程度。ANN的突触（权值）仅仅由一个数值量描述，而生物神经元突触是复杂的动态系统。具有化学性质的突触利用分子机构，每个突触都是很高维的状态空间，因此生物突触在时间与空间尺度都具有很大的可塑性。生物突触的这种复杂性被猜测是用来（有助于）巩固记忆的。在ANN领域，已经有研究尝试解释增加的突触复杂性是如何有益于神经网络模型在多任务下的有监督学习。

由于简单的常量一维突触具有灾难性遗忘的问题，即神经网络在学习新任务时会遗忘之前所学过的任务。为此我们扩增了人工神经元状态空间的维度，增加为三维：当前的参数值、上一时刻的参数值、以及第个突触的重要性（对于之前的任务）。该重要性测度可以对于每个突触局部的计算。这个重要性表示每个突触改变影响全局loss变化的程度。

论文的核心思想是：在训练任务的过程中，度量每个突触的重要性；并在训练新任务时，利用该重要性来惩罚重要权值的变化，从而避免历史记忆被覆盖。

2. 怎么度量突触的重要性

神经网络的训练过程（特别是基于迭代的BP算法）可以由一条在参数空间的轨迹$\theta (t)$来描述。如果参数轨迹的最终点落在使损失函数$L$达到最小值的附近时，说明训练成功。

对于一个神经网络，它由若干神经元与关联神经的参数组成。首先，我们假定网络的参数在时间$t$有一个微量的变化$\delta (t)$（这模拟了一次训练对参数的更新），然后我们可以计算损失函数在参数变化前、后的值，由此可得对某一参数的微量调整，对损失函数的影响程度。损失函数的变化可以由梯度$g=\frac{\partial L}{\partial \theta }$近似表示，具体损失函数的变化公式如下：
$$L(\theta (t)+\delta (t))-L(\theta (t))\approx \sum _k{g}_k(t){\delta }_k(t)\text{\hspace{1em}(1)}$$
上面式子表示每个参数的变化${\delta }_k(t)={\theta }_t^{\prime }(t)$引起损失函数的变化量为$g_k(t){\delta }_k(t)$。

为了计算参数在参数空间中按某条轨迹对损失函数造成的所有微小变化的总和，我们需要计算参数轨迹在梯度上的路徑积分

$${\int }_{C}g(\theta (t))d\theta ={\int }_{t_0}^{t_1}g(\theta (t)){\theta }^{\prime }(t)dt=L(\theta (t_1))-L(\theta (t_0))\text{\hspace{1em}(2)}$$

为了能够计算单个权值的改变对损失函数的影响，可将式(2)改成下式
$${\int }_{t^{\mu -1}}^{t^{\mu }}g(\theta (t)){\theta }^{\prime }(t)dt=\sum _k{\int }_{t^{\mu -1}}^{t^{\mu }}{g}_k(\theta (t)){\theta }_k^{\prime }(t)dt=-\sum _k{\omega }_k^{\mu }\text{\hspace{1em}(3)}$$
其中，$-{\omega }_k^{\mu }$就是第$k$个权值的调整对损失函数的影响。

在实际情况中，我们可以对训练过程中产生的梯度与参数更新量的积进行累加来近似${\omega }_k^{\mu }$。

上面讲的有情（文字）有理（公式）：参数的微小调整会造成损失值的变化，也给出了计算公式。

但是，以上获取的信息怎么上升到知识的层面，也即怎么提升神经网络的多任务（本人仍坚持多任务学习不能等同于连续学习）学习能力。
[论文原句]How can the knowledge of ${\omega }_k^{\mu }$ be exploited to improve continual learning?

作者回答：我们假定在训练任务$\mu$时，各权值的路径积分为${\omega }_k^{\mu }$。在训练过程中，${\omega }_k^{\mu }$越大，说明在任务$\mu$训练中调整越大，间接的说明${\omega }_k^{\mu }$对任务$\mu$来说很重要。

类比人，我们为了适应新的环境而做出各方面的改变，假定我们最终适应了该环境 ，则其中改变最大的一面对我们是否能适应该环境的重要性最大。

过度的有点突兀，哈哈哈…

训练时的权值路径积分可用来作为度量该权值相对该任务重要的重要依据。积分值越大，说明对于该任务，该权值的重要性也越大。

在论文中，权值的重要性由以下公式度量：
$${\Omega }_k^{\mu }=\sum _{v<\mu }\frac{{\omega }_k^v}{({\Delta }_k^v{)}^2+\xi }\text{\hspace{1em}(4)}$$

其中，${\Delta }_k^v={\theta }_k(t^v)-{\theta }_k(t^{v-1})$是为了确保正则项具有与损失函数相同的单位尺度。参数$\xi$是为了防止${\Delta }_k^v$接近零时造成的计算BUG。在训练某一任务时，${\omega }_k^{\mu }$一更新，${\Omega }_k^{\mu }$与$\hat{\theta }$仅仅在前一个任务结束与新任务开始前更新，并且在更新${\Omega }_k^{\mu }$后，${\omega }_k$重置为0。

我们将权值的重要性${\Omega }_k^{\mu }$加入代价函数中：

$$\widehat{L_{\mu }}=L_{\mu }+c\sum _k{\Omega }_k^{\mu }({\hat{\theta }}_k-{\theta }_k{)}^2\text{\hspace{1em}(5)}$$

其中，${\hat{\theta }}_k={\theta }_k^{\mu -1}$，也即上一个任务训练结束后的权值。

新构造的代价函数根据权值相对历史任务的重要程度信息来抑制相重要权值的调整，越重要的权值，让其保持更小的变化。（这是正则化项的作用）

作者还在论文中对权值路径积分进行了理论分析（我不想看，头痛！），还跟Fisher information进行了对比。感兴趣的铜鞋可以去康康。

3.代码怎么啃–一行一行啃

作者将论文代码开源在GitHub上[ganguli-lab/pathint/github]。(https://github.com/ganguli-lab/pathint)。程序是基于keras写的，首先得熟悉keras的backend模块。然后才能顺利读懂作者的开源代码。

3.1 Keras自定义优化器

我们先来熟悉keras的backend模块，看看怎么对自己定义的loss函数实现专门的优化器。首先感谢这篇博客用时间换取效果：Keras梯度累积优化器。

3.1.1 父类优化器Optimizer

keras中定义了一些优化器，例如：SGD，RMSprop，Adagrad，Adadelta，Adam，Adamax，Nadam，TFOptimizer等。他们都有一个共同的父类，就是Optimizer。Optimizer给出了优化器的骨架，每个具体的优化器只是肉身不同而已，高、矮
、胖、瘦。优化器中最主要的两个函数是__init__与get_updates。不同的优化器，初始化函数传入的参数是不一样的，我们也可以根据需要自己添加额外的输入参数。不同的优化器的更新函数也是不一样的。子类继承主要是这两个函数的变化，以及其他附加功能函数的。父类优化器中的get_updates函数是空着的，只预留了个函数位置，等子类实现。下面讲解的所有具体优化器都只讲解这两个函数与一些重要的附加功能函数。

class Optimizer(object):
    """Abstract optimizer base class.
    Note: this is the parent class of all optimizers, not an actual optimizer
    that can be used for training models.
    All Keras optimizers support the following keyword arguments:
        clipnorm: float >= 0. Gradients will be clipped
            when their L2 norm exceeds this value.
        clipvalue: float >= 0. Gradients will be clipped
            when their absolute value exceeds this value.
    """

    def __init__(self, **kwargs):
        allowed_kwargs = {
     'clipnorm', 'clipvalue'}
        for k in kwargs:
            if k not in allowed_kwargs:
                raise TypeError('Unexpected keyword argument '
                                'passed to optimizer: ' + str(k))
        self.__dict__.update(kwargs)
        self.updates = []
        self.weights = []

    @interfaces.legacy_get_updates_support
    @K.symbolic
    def get_updates(self, loss, params):
        raise NotImplementedError

    def get_gradients(self, loss, params):
        grads = K.gradients(loss, params)
        if any(x is None for x in grads):
            raise ValueError('An operation has `None` for gradient. '
                             'Please make sure that all of your ops have a '
                             'gradient defined (i.e. are differentiable). '
                             'Common ops without gradient: '
                             'K.argmax, K.round, K.eval.')
        if hasattr(self, 'clipnorm') and self.clipnorm > 0:
            norm = K.sqrt(sum([K.sum(K.square(g)) for g in grads]))
            grads = [clip_norm(g, self.clipnorm, norm) for g in grads]
        if hasattr(self, 'clipvalue') and self.clipvalue > 0:
            grads = [K.clip(g, -self.clipvalue, self.clipvalue) for g in grads]
        return grads

    def set_weights(self, weights):
        """Sets the weights of the optimizer, from Numpy arrays.
        Should only be called after computing the gradients
        (otherwise the optimizer has no weights).
        # Arguments
            weights: a list of Numpy arrays. The number
                of arrays and their shape must match
                number of the dimensions of the weights
                of the optimizer (i.e. it should match the
                output of `get_weights`).
        # Raises
            ValueError: in case of incompatible weight shapes.
        """
        params = self.weights
        if len(params) != len(weights):
            raise ValueError('Length of the specified weight list (' +
                             str(len(weights)) +
                             ') does not match the number of weights ' +
                             'of the optimizer (' + str(len(params)) + ')')
        weight_value_tuples = []
        param_values = K.batch_get_value(params)
        for pv, p, w in zip(param_values, params, weights):
            if pv.shape != w.shape:
                raise ValueError('Optimizer weight shape ' +
                                 str(pv.shape) +
                                 ' not compatible with '
                                 'provided weight shape ' + str(w.shape))
            weight_value_tuples.append((p, w))
        K.batch_set_value(weight_value_tuples)

    def get_weights(self):
        """Returns the current value of the weights of the optimizer.
        # Returns
            A list of numpy arrays.
        """
        return K.batch_get_value(self.weights)

    def get_config(self):
        config = {
     }
        if hasattr(self, 'clipnorm'):
            config['clipnorm'] = self.clipnorm
        if hasattr(self, 'clipvalue'):
            config['clipvalue'] = self.clipvalue
        return config

    @classmethod
    def from_config(cls, config):
        return cls(**config)

    @property
    def lr(self):
        # Legacy support.
        return self.learning_rate

3.1.2 一个简单的优化器实例SGD

随机梯度下降是最简单的优化器。初始化函数的入口参数有学习率、学习率的率减参数、以及防止计算BUG的小常值。

• 初始化函数

    def __init__(self, learning_rate=0.01, **kwargs):
        self.initial_decay = kwargs.pop('decay', 0.0)
        self.epsilon = kwargs.pop('epsilon', K.epsilon())
        learning_rate = kwargs.pop('lr', learning_rate)
        super(Adagrad, self).__init__(**kwargs)
        with K.name_scope(self.__class__.__name__):
            self.learning_rate = K.variable(learning_rate, name='learning_rate')
            self.decay = K.variable(self.initial_decay, name='decay')
            self.iterations = K.variable(0, dtype='int64', name='iterations')

在更新函数中，Listupdates存储所有需要更新的量，底层会一起更新。例如，函数中：
self.updates = [K.update_add(self.iterations, 1)]
self.updates.append(K.update(p, new_p))
就是分别对迭代次数、权值进行更新。我们不需要管它是怎么实现更新，只需要把每要更新的放入这个列表中即可。

• get_updates函数

    def get_updates(self, loss, params):
        grads = self.get_gradients(loss, params)
        shapes = [K.int_shape(p) for p in params]
        accumulators = [K.zeros(shape, name='accumulator_' + str(i))
                        for (i, shape) in enumerate(shapes)]
        self.weights = [self.iterations] + accumulators
        self.updates = [K.update_add(self.iterations, 1)]

        lr = self.learning_rate
        if self.initial_decay > 0:
            lr = lr * (1. / (1. + self.decay * K.cast(self.iterations,
                                                      K.dtype(self.decay))))

        for p, g, a in zip(params, grads, accumulators):
            new_a = a + K.square(g)  # update accumulator
            self.updates.append(K.update(a, new_a))
            new_p = p - lr * g / (K.sqrt(new_a) + self.epsilon)

            # Apply constraints.
            if getattr(p, 'constraint', None) is not None:
                new_p = p.constraint(new_p)

            self.updates.append(K.update(p, new_p))
        return self.

3.1.3 定义自己的优化器

写用时间换取效果：Keras梯度累积优化器的博主很优秀，也将代码Push到了github，地址：bojone/accum_optimizer_for_keras。里面程序写的很简洁，很容易读，懂不懂就因人而异。理解tensorflow计算图的话，就非常容易看懂。博主还给了示例程序，建议大家跑一下，加深理解。我跑了半个小时，还只跑了1/10，果断停了，验证了算法有效，程序没错就可以了，自己电脑跑图片数据集还是有点吃力呀！

博主为了实现软batch，也即每次batch_size=1，只利用一个数据输入网络得到梯度值，但是又为了达到批处理的训练收敛稳定性效果，每次只计算梯度，然后累加，直到累积次数达到预设定的软batch_size大小，则利用累积的梯度更新权值一次。就像该博文的题目：用时间换取效果（空间）。这降低了对GPU的依赖性。本文不评价这种作法的合理性，只是单纯用来熟悉如何在keras中定义自己的优化器。如果，我们是做机器学习的，研究的比较深时，都会设计自己的优化器，如果不知道怎么实现就会很被动。自己从头开始写一个神经网络？还是饶了你自己吧！

#! -*- coding: utf-8 -*-

from keras.optimizers import Optimizer
import keras.backend as K


class AccumOptimizer(Optimizer):
    """继承Optimizer类，包装原有优化器，实现梯度累积。
    # 参数
        optimizer：优化器实例，支持目前所有的keras优化器；
        steps_per_update：累积的步数。
    # 返回
        一个新的keras优化器
    Inheriting Optimizer class, wrapping the original optimizer
    to achieve a new corresponding optimizer of gradient accumulation.
    # Arguments
        optimizer: an instance of keras optimizer (supporting
                    all keras optimizers currently available);
        steps_per_update: the steps of gradient accumulation
    # Returns
        a new keras optimizer.
    """
    def __init__(self, optimizer, steps_per_update=1, **kwargs):
        super(AccumOptimizer, self).__init__(**kwargs)
        self.optimizer = optimizer
        with K.name_scope(self.__class__.__name__):
            self.steps_per_update = steps_per_update
            self.iterations = K.variable(0, dtype='int64', name='iterations')
            self.cond = K.equal(self.iterations % self.steps_per_update, 0)
            self.lr = self.optimizer.lr
            self.optimizer.lr = K.switch(self.cond, self.optimizer.lr, 0.)
            for attr in ['momentum', 'rho', 'beta_1', 'beta_2']:
                if hasattr(self.optimizer, attr):
                    value = getattr(self.optimizer, attr)
                    setattr(self, attr, value)
                    setattr(self.optimizer, attr, K.switch(self.cond, value, 1 - 1e-7))
            for attr in self.optimizer.get_config():
                if not hasattr(self, attr):
                    value = getattr(self.optimizer, attr)
                    setattr(self, attr, value)
            # 覆盖原有的获取梯度方法，指向累积梯度
            # Cover the original get_gradients method with accumulative gradients.
            def get_gradients(loss, params):
                return [ag / self.steps_per_update for ag in self.accum_grads]
            self.optimizer.get_gradients = get_gradients
    def get_updates(self, loss, params):
        self.updates = [
            K.update_add(self.iterations, 1),
            K.update_add(self.optimizer.iterations, K.cast(self.cond, 'int64')),
        ]
        # 累积梯度 (gradient accumulation)
        self.accum_grads = [K.zeros(K.int_shape(p), dtype=K.dtype(p)) for p in params]
        grads = self.get_gradients(loss, params)
        for g, ag in zip(grads, self.accum_grads):
            self.updates.append(K.update(ag, K.switch(self.cond, ag * 0, ag + g)))
        # 继承optimizer的更新 (inheriting updates of original optimizer)
        self.updates.extend(self.optimizer.get_updates(loss, params)[1:])
        self.weights.extend(self.optimizer.weights)
        return self.updates
    def get_config(self):
        iterations = K.eval(self.iterations)
        K.set_value(self.iterations, 0)
        config = self.optimizer.get_config()
        K.set_value(self.iterations, iterations)
        return config

为了实现通过累积单次梯度的方式来实现软Batch训练，初始化函数中新加入了优化器变量optimizer（博主用的是Adam）与参数cond。其中，cond表示当前步是否达到预定的累积batch_size，如果达到则该值为true,否则为false。在初始化函数中还定义了新的获取梯度的函数（因为此处我们是通过累积梯度来计算），并将新定义的获取梯度函数赋给self.optimizer.get_gradients，也即Keras实现的Adam类中的get_gradients函数重定义（如下）。

def get_gradients(loss, params):
    return [ag / self.steps_per_update for ag in self.accum_grads]
self.optimizer.get_gradients = get_gradients    

在更新函数里面，也用到了一个获取梯度的函数。self.optimizer.get_gradients与self.get_gradients是不同的。前者是传入优化器Adam中的获取梯度函数，而后者是新定义的优化器中的获取梯度函数。

[非常重要] 注释：该新定义的优化器参数中又包含优化器，还是比较有意思的。新定义的优化器不光从类上继承了optimizer，还以同样以optimizer为父类的Adam优化器作为输入。因此新的优化器中总共有两套完整的优化器。self.optimizer.get_gradients与self.get_gradients，又有self.optimizer.get_updates与self.get_updates。我们读程序的时候只需要注意函数前面表示的是传入的优化器，还是新定义的优化器本身，就不会搞迷糊了。

在初始化函数中，变量self.cond与self.optimizer.lr被写进了tensorflow图里面，每次相应变量改变，这些变量的值也会随着自动更新。在get_updates函数里，会显示的将迭代次数变量self.iterations进行更新，因此，下面的变量值在每一步都会得到更新。值得注意的是，self.cond确定累积是否到达软batch_size，如达到则学习率为self.optimizer.lr，否则为0。这间接的让优化器达到，在累积期间不进行训练（学习率为0），在累积满后训练一次，并重新从0累积。

self.cond = K.equal(self.iterations % self.steps_per_update, 0)
self.lr = self.optimizer.lr
self.optimizer.lr = K.switch(self.cond, self.optimizer.lr, 0.)

新的优化器的更新函数中，将所有需要更新的变量都放入到列表self.updates中，主要有迭代次数变量，累积梯度，Adam更新参数函数。注意，在初始化函数中，已经将传入优化器Adam的get_gradient函数，以及学习率lr进行了重新定义。就拿学习率来说，它有时取零，有时取正常的有意义的学习率。取得梯度的函数也是初始化函数中新定义的得到平均累积梯度值的函数。

self.updates = [
     K.update_add(self.iterations, 1),
     K.update_add(self.optimizer.iterations, K.cast(self.cond, 'int64')),
]
for g, ag in zip(grads, self.accum_grads):
	self.updates.append(K.update(ag, K.switch(self.cond, ag * 0, ag + g)))
self.updates.extend(self.optimizer.get_updates(loss, params)[1:])	

如果理解tensorflow的计算图的概念，读这些程序会轻松些。如果不理解tf的计算图的概念，我们可以把整个程序看作一个静态的从上到下的有向图，上面的节点输出作为下一层节点的输入。图中一旦有某个节点的值进行了更新，以他为祖先节点的节点值都会更新。get_update函数返回的列表updates中都是需要更新的节点，与这些更新节点相关的节点都会自动更新。这就是TF的计算图。

3.2 Pathint|GitHub

以上讲这么多，都只是为了缓冲，只是为了见到下面这个怪物能自信一点。好难啊！这个程序把我看的觉得世界都灰暗了。读了整整三天这个程序，从头到尾（自以为）的看了五、六遍。每个字母都认得，就是没看懂这个类怎么就能完成论文里所说的方法了。论文里的最终公式就两个：1）新的损失函数；2）权值重要性$\omega$。程序为啥就看不懂了。不过，现在回头再读，真的很容易。那几个关键的点通了，就顺畅了。堵住我的几个关键点为：1）tensorflow计算图概念不清楚；2）由迷茫衍生出的粗心大意。前者通过上面几个例子的分析，已经够我理解这个程序了。现在将我粗心的地方着重列出，供大家参照，以免重走十八绕。

# Copyright (c) 2017 Ben Poole & Friedemann Zenke
# MIT License -- see LICENSE for details
# 
# This file is part of the code to reproduce the core results of:
# Zenke, F., Poole, B., and Ganguli, S. (2017). Continual Learning Through
# Synaptic Intelligence. In Proceedings of the 34th International Conference on
# Machine Learning, D. Precup, and Y.W. Teh, eds. (International Convention
# Centre, Sydney, Australia: PMLR), pp. 3987-3995.
# http://proceedings.mlr.press/v70/zenke17a.html
#
"""Optimization algorithms."""

import tensorflow as tf

import numpy as np
import keras
from keras import backend as K
from keras.optimizers import Optimizer
from keras.callbacks import Callback
from pathint.utils import extract_weight_changes, compute_updates
from pathint.regularizers import quadratic_regularizer
from collections import OrderedDict


class KOOptimizer(Optimizer):
    """An optimizer whose loss depends on its own updates."""

    def _allocate_var(self, name=None):
        return {
     w: K.zeros(w.get_shape(), name=name) for w in self.weights}

    def _allocate_vars(self, names):
        #TODO: add names, better shape/init checking
        self.vars = {
     name: self._allocate_var(name=name) for name in names}

    def __init__(self, opt, step_updates=[], task_updates=[], init_updates=[], task_metrics = {
     }, regularizer_fn=quadratic_regularizer,
                lam=1.0, model=None, compute_average_loss=False, compute_average_weights=False, **kwargs):
        """Instantiate an optimzier that depends on its own updates.

        Args:
            opt: Keras optimizer
            step_updates: OrderedDict or List of tuples
                Contains variable names and updates to be run at each step:
                (name, lambda vars, weight, prev_val: new_val). See below for details.
            task_updates:  same as step_updates but run after each task
            init_updates: updates to be run before using the optimizer
            task_metrics: list of names of metrics to compute on full data/unionset after a task
            regularizer_fn (optional): function, takes in weights and variables returns scalar
                defaults to EWC regularizer
            lam: scalar penalty that multiplies the regularization term
            model: Keras model to be optimized. Needed to compute Fisher information
            compute_average_loss: compute EMA of the loss, default: False
            compute_average_weights: compute EMA of the weights, default: False

        Variables are created for each name in the task and step updates. Note that you cannot
        use the name 'grads', 'unreg_grads' or 'deltas' as those are reserved to contain the gradients
        of the full loss, loss without regularization, and the weight updates at each step.
        You can access them in the vars dict, e.g.: oopt.vars['grads']

        The step and task update functions have the signature:
            def update_fn(vars, weight, prev_val):
                '''Compute the new value for a variable.
                Args:
                    vars: optimization variables (OuroborosOptimzier.vars)
                    weight: weight Variable in model that this variable is associated with.
                    prev_val: previous value of this varaible
                Returns:
                    Tensor representing the new value'''

        You can run both task and step updates on the same variable, allowing you to reset
        step variables after each task.
        """
        super(KOOptimizer, self).__init__(**kwargs)
        if not isinstance(opt, keras.optimizers.Optimizer):
            raise ValueError("opt must be an instance of keras.optimizers.Optimizer but got %s"%type(opt))
        if not isinstance(step_updates, OrderedDict):
            step_updates = OrderedDict(step_updates)
        if not isinstance(task_updates, OrderedDict): task_updates = OrderedDict(task_updates)
        if not isinstance(init_updates, OrderedDict): init_updates = OrderedDict(init_updates)
        # task_metrics
        self.names = set().union(step_updates.keys(), task_updates.keys(), task_metrics.keys())
        if 'grads' in self.names or 'deltas' in self.names:
            raise ValueError("Optimization variables cannot be named 'grads' or 'deltas'")
        self.step_updates = step_updates
        self.task_updates = task_updates
        self.init_updates = init_updates
        self.compute_average_loss = compute_average_loss
        self.regularizer_fn = regularizer_fn
        # Compute loss and gradients
        self.lam = K.variable(value=lam, dtype=tf.float32, name="lam")
        self.nb_data = K.variable(value=1.0, dtype=tf.float32, name="nb_data")
        self.opt = opt
        #self.compute_fisher = compute_fisher
        #if compute_fisher and model is None:
        #    raise ValueError("To compute Fisher information, you need to pass in a Keras model object ")
        self.model = model
        self.task_metrics = task_metrics
        self.compute_average_weights = compute_average_weights

    def set_strength(self, val):
        K.set_value(self.lam, val)

    def set_nb_data(self, nb):
        K.set_value(self.nb_data, nb)

    def get_updates(self, params,loss,model=None):
        self.weights = params
        # Allocate variables
        with tf.variable_scope("KOOptimizer"):
            self._allocate_vars(self.names)

        #grads = self.get_gradients(loss, params)

        # Compute loss and gradients
        self.regularizer = 0.0 if self.regularizer_fn is None else self.regularizer_fn(params, self.vars)
        self.initial_loss = loss
        self.loss = loss + self.lam * self.regularizer
        with tf.variable_scope("wrapped_optimizer"):
            self._weight_update_op, self._grads, self._deltas = compute_updates(self.opt, self.loss, params)

        wrapped_opt_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, "wrapped_optimizer")
        self.init_opt_vars = tf.variables_initializer(wrapped_opt_vars)

        self.vars['unreg_grads'] = dict(zip(params, tf.gradients(self.initial_loss, params)))
        # Compute updates
        self.vars['grads'] = dict(zip(params, self._grads))
        self.vars['deltas'] = dict(zip(params, self._deltas))
        # Keep a pointer to self in vars so we can use it in the updates
        self.vars['oopt'] = self
        # Keep number of data samples handy for normalization purposes
        self.vars['nb_data'] = self.nb_data

        if self.compute_average_weights:
            with tf.variable_scope("weight_emga") as scope:
                weight_ema = tf.train.ExponentialMovingAverage(decay=0.99, zero_debias=True)
                self.maintain_weight_averages_op = weight_ema.apply(self.weights)
                self.vars['average_weights'] = {
     w: weight_ema.average(w) for w in self.weights}
            self.weight_ema_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope=scope.name)
            self.init_weight_ema_vars = tf.variables_initializer(self.weight_ema_vars)
            print(">>>>>")
            K.get_session().run(self.init_weight_ema_vars)
        if self.compute_average_loss:
            with tf.variable_scope("ema") as scope:
                ema = tf.train.ExponentialMovingAverage(decay=0.99, zero_debias=True)
                self.maintain_averages_op = ema.apply([self.initial_loss])
                self.ema_loss = ema.average(self.initial_loss)
                self.prev_loss = tf.Variable(0.0, trainable=False, name="prev_loss")
                self.delta_loss = tf.Variable(0.0, trainable=False, name="delta_loss")
            self.ema_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope=scope.name)
            self.init_ema_vars = tf.variables_initializer(self.ema_vars)
#        if self.compute_fisher:
#            self._fishers, _, _, _ = compute_fishers(self.model)
#            #fishers = compute_fisher_information(model)
#            self.vars['fishers'] = dict(zip(weights, self._fishers))
#            #fishers, avg_fishers, update_fishers, zero_fishers = compute_fisher_information(model)

        def _var_update(vars, update_fn):
            updates = []
            for w in params:
                updates.append(tf.assign(vars[w], update_fn(self.vars, w, vars[w])))
            return tf.group(*updates)

        def _compute_vars_update_op(updates):
            # Force task updates to happen sequentially
            update_op = tf.no_op()
            for name, update_fn in updates.items():
                with tf.control_dependencies([update_op]):
                    update_op = _var_update(self.vars[name], update_fn)
            return update_op

        self._vars_step_update_op = _compute_vars_update_op(self.step_updates)
        self._vars_task_update_op = _compute_vars_update_op(self.task_updates)
        self._vars_init_update_op = _compute_vars_update_op(self.init_updates)

        # Create task-relevant update ops
        reset_ops = []
        update_ops = []
        for name, metric_fn in self.task_metrics.items():
            metric = metric_fn(self)
            for w in params:
                reset_ops.append(tf.assign(self.vars[name][w], 0*self.vars[name][w]))
                update_ops.append(tf.assign_add(self.vars[name][w], metric[w]))
        self._reset_task_metrics_op = tf.group(*reset_ops)
        self._update_task_metrics_op = tf.group(*update_ops)

        # Each step we update the weights using the optimizer as well as the step-specific variables
        self.step_op = tf.group(self._weight_update_op, self._vars_step_update_op)
        self.updates.append(self.step_op)
        # After each task, run task-specific variable updates
        self.task_op = self._vars_task_update_op
        self.init_op = self._vars_init_update_op

        if self.compute_average_weights:
            self.updates.append(self.maintain_weight_averages_op)

        if self.compute_average_loss:
            self.update_loss_op = tf.assign(self.prev_loss, self.ema_loss)
            bupdates = self.updates
            with tf.control_dependencies(bupdates + [self.update_loss_op]):
                self.updates = [tf.group(*[self.maintain_averages_op])]
            self.delta_loss = self.prev_loss - self.ema_loss

        return self.updates#[self._base_updates

    def init_task_vars(self):
        K.get_session().run([self.init_op])

    def init_acc_vars(self):
        K.get_session().run(self.init_ema_vars)

    def init_loss(self, X, y, batch_size):
        pass
        #sess = K.get_session()
        #xi, yi, sample_weights = self.model.model._standardize_user_data(X[:batch_size], y[:batch_size], batch_size=batch_size)
        #sess.run(tf.assign(self.prev_loss, self.initial_loss), {self.model.input:xi[0], self.model.model.targets[0]:yi[0], self.model.model.sample_weights[0]:sample_weights[0], K.learning_phase():1})

    def update_task_vars(self):
        K.get_session().run(self.task_op)

    def update_task_metrics(self, X, y, batch_size):
        # Reset metric accumulators
        n_batch = len(X) // batch_size

        sess = K.get_session()
        sess.run(self._reset_task_metrics_op)
        for i in range(n_batch):
            xi, yi, sample_weights = self.model._standardize_user_data(X[i * batch_size:(i+1) * batch_size], y[i*batch_size:(i+1)*batch_size], batch_size=batch_size)
            sess.run(self._update_task_metrics_op, {
     self.model.input:xi[0], self.model.targets[0]:yi[0], self.model.sample_weights[0]:sample_weights[0]})


    def reset_optimizer(self):
        """Reset the optimizer variables"""
        K.get_session().run(self.init_opt_vars)

    def get_config(self):
        raise ValueError("Write the get_config bro")

    def get_numvals_list(self, key='omega'):
        """ Returns list of numerical values such as for instance omegas in reproducible order """
        variables = self.vars[key]
        numvals = []
        for p in self.weights:
            numval = K.get_value(tf.reshape(variables[p],(-1,)))
            numvals.append(numval)
        return numvals

    def get_numvals(self, key='omega'):
        """ Returns concatenated list of numerical values such as for instance omegas in reproducible order """
        conc = np.concatenate(self.get_numvals_list(key))
        return conc

    def get_state(self):
        state = []
        vs = self.vars
        for key in vs.keys():
            if key=='oopt': continue
            v = vs[key]
            for p in v.values():
                state.append(K.get_value(p)) # FIXME WhyTF does this not work?
        return state

    def set_state(self, state):
        c = 0
        vs = self.vars
        for key in vs.keys():
            if key=='oopt': continue
            v = vs[key]
            for p in v.values():
                K.set_value(p,state[c])
                c += 1

初始化的传入参数没有仔细看，以为step_updates，task_updates这些都是一个空列表，等待初始化，或后面用到时往里append元素。找了几遍，都发现这个值自始致终没有被传入元素，但是训练时需要对与任务相关以及每步相关的参数进行分别更新，这啥也没有，程序是如何做到训练成功的呢（我在读程序前，跑通了程序，效果还不错）？很纳闷。

def __init__(self, opt, step_updates=[], task_updates=[], init_updates=[], task_metrics = {
     }, regularizer_fn=quadratic_regularizer,
                lam=1.0, model=None, compute_average_loss=False, compute_average_weights=False, **kwargs):

就在昨天，我发现，示例程序中对新定义的优化器进行实体化时，后面的**protocol里传入哪些参数呢？

protocol_name, protocol = protocols.PATH_INT_PROTOCOL(omega_decay='sum', xi=xi)
oopt = KOOptimizer(opt, model=model, **protocol)

之前一直忽视了，没去它在哪。专门注意到后，找还是很容易的。它的定义如下（我们可以找到权值重要性指标$\omega$就在protocol里）：

PATH_INT_PROTOCOL = lambda omega_decay, xi: (
        'path_int[omega_decay=%s,xi=%s]'%(omega_decay,xi),
{
     
    'init_updates':  [
        ('cweights', lambda vars, w, prev_val: w.value() ),
        ],
    'step_updates':  [
        ('grads2', lambda vars, w, prev_val: prev_val -vars['unreg_grads'][w] * vars['deltas'][w] ),
        ],
    'task_updates':  [
        ('omega',     lambda vars, w, prev_val: tf.nn.relu( ema(omega_decay, prev_val, vars['grads2'][w]/((vars['cweights'][w]-w.value())**2+xi)) ) ),
        #('cached_grads2', lambda vars, w, prev_val: vars['grads2'][w]),
        #('cached_cweights', lambda vars, w, prev_val: vars['cweights'][w]),
        ('cweights',  lambda opt, w, prev_val: w.value()),
        ('grads2', lambda vars, w, prev_val: prev_val*0.0 ),
    ],
    'regularizer_fn': quadratic_regularizer,
})

然后衔接上tensorflow的计算图，所有的都通了。这是一个不难的程序，但前提是懂tensorflow的计算图的概念，并且细心点。奈何，计算图已经把我的耐心耗的差不多，等懂了计算图，又变得粗心大意。唉！我真好难啊！太难啦！

下面是跑的最终结果，作者的示例程序用minist数据集。

4.总结

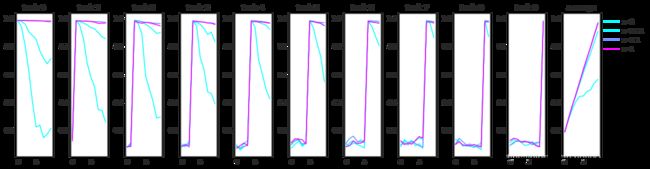
本文从思想、方法、算法（公式）、程序四个层次对论文[1]进行了解析。文章开头本人小小的吐嘈了下作者论文题目的修改。Multitask Learning比Continual Learning更符合论文的实际内容。但是作者还是选择了看起来更加高级的Continual Learning。首先，得承认论文方法是优质的，能经过ICML检验的论文能差到哪儿去，并且如果我认为论文不好，还会花这么时间去精读吗？更别说写这篇博客啦！我专门拿题目来说，只是觉得这是一个值得关注、值得对自己喜欢的一篇论文贴上一个不十全十美标签的问题。人类为什么花这么大精力去定义、分类？就是为了信息传递时熵降到最小。我们能用最简单的话，把足够多的信息足够准确的传递给他人。我觉得越是好的论文，越应该注意这个问题，因为受众很多。在严格定义上，我个人认为多任务学习还不能被称为连续学习，特别是论文[1]中的方法所必需要的训练模式更不能称之为连续学习。连续学习得具备对新数据进行学习的能力，论文中的方法只是具有对新任务的学习能力。不具备对新数据学习的能力。举个例子，假定已经学习了任务1，论文[1]方法可以使AI继续学任务2,并且不会产生太大的灾难性遗忘，基本保有之前所学的任务知识。但是，此刻来了与任务1相关的新的数据，并且该数据作为任务1之前未考虑到的场景，是必需学习的新案例。此时，直接让其输入到神经网络训练？这是难为它了，因为方法根本没考虑上面描述的情况。现有的缓解深度学习灾难性遗忘问题的方法都存在这个不足，回避了这个问题。回避就回避吧，用一个多任务学习作题目就好了，为什么一定要用连续学习、终身学习、增量式学习这样与方法不怎么般配的题目呢？下面的截图是我开始读论文[1]时做的笔记，开头我是想好好做笔记的，可是写着写着，话风就变了，变成了吐嘈。回头看，自己都觉得搞笑。不得不说，方法是好的，值得学习。但是题目容易让大家认为这样的学习就是连续学习，就是终身学习，并且形成先入为主的概念，反倒觉得这就是定理，真理啦！我觉得这一点是不好的。

以上仅个人观点，欢迎留言，反驳，交流！

[1]F. Zenke, B. Poole, and S. Ganguli, “Continual Learning Through Synaptic Intelligence,” arXiv:1703.04200 [cs, q-bio, stat], Mar. 2017.