LeetCode第160场周赛(Weekly Contest 160)解题报告
这周的周赛,惨不忍睹,隔了好久.排名:429 / 1691。写题的时候,第二题我以为答案是不唯一的,没想到是唯一答案,所以我就心态爆炸了,其实第二题就是一个格雷码的问题,而格雷码一般认为是“典型格雷码”,所以是唯一的。然后心态就爆炸了,第三题都不想做了,哈哈哈
第一题,暴力枚举即可,只是题目比较长,学会调用那个类就可以了。
第二题,关于格雷码的,其实很简单。
第三题,由于字符串的长度是16,每一个字符串有两种情况,要或不要,所以直接可以DFS,时间不会超
第四题,神仙题,好像涉及了很复杂的东西,我就没去看了,有一些人就打表提交,有一些人暴力,有一些人是有原理的,具体我贴链接在后面,大家感兴趣的可以点进去看。
详细题解如下。
1. 找出给定方程的正整数解(Find Positive Integer Solution for A Given Equation)
AC代码(C++)
2. 循环码排列(Circular Permutation in Binary Representation)
AC代码(C++)
3.串联字符串的最大长度(Maximum Length of A Concatenated String with Unique Characters)
AC代码(C++)
4.铺瓷砖(Tiling A Rectangle with the Fewest Squares)
AC代码(C++)
LeetCode第160场周赛地址:
https://leetcode-cn.com/contest/weekly-contest-160
1. 找出给定方程的正整数解(Find Positive Integer Solution for A Given Equation)
题目链接
https://leetcode-cn.com/contest/weekly-contest-160/problems/find-positive-integer-solution-for-a-given-equation/
题意
给出一个函数
f(x, y)和一个目标结果z,请你计算方程f(x,y) == z所有可能的正整数 数对x和y。给定函数是严格单调的,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)函数接口定义如下:
interface CustomFunction { public: // Returns positive integer f(x, y) for any given positive integer x and y. int f(int x, int y); };如果你想自定义测试,你可以输入整数
function_id和一个目标结果z作为输入,其中function_id表示一个隐藏函数列表中的一个函数编号,题目只会告诉你列表中的2个函数。你可以将满足条件的 结果数对 按任意顺序返回。
示例 1:
输入:function_id = 1, z = 5 输出:[[1,4],[2,3],[3,2],[4,1]] 解释:function_id = 1 表示 f(x, y) = x + y示例 2:
输入:function_id = 2, z = 5 输出:[[1,5],[5,1]] 解释:function_id = 2 表示 f(x, y) = x * y提示:
1 <= function_id <= 91 <= z <= 100- 题目保证
f(x, y) == z的解处于1 <= x, y <= 1000的范围内。- 在
1 <= x, y <= 1000的前提下,题目保证f(x, y)是一个 32 位有符号整数。
解题思路
根据提示,题目的解 x,y 在 [1, 1000],那么我们如果暴力枚举,那么复杂度为O(n^2)
并不会超时。
同时由于函数是严格单调递增的,如果对于某一个 x 下,枚举 y 的时候,函数值已经超过 z 了,表示剩下的 y 都不满足,直接可以枚举 下一个 x。这样子可以减少枚举次数。
AC代码(C++)
/*
* // This is the custom function interface.
* // You should not implement it, or speculate about its implementation
* class CustomFunction {
* public:
* // Returns f(x, y) for any given positive integers x and y.
* // Note that f(x, y) is increasing with respect to both x and y.
* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)
* int f(int x, int y);
* };
*/
class Solution {
public:
vector> findSolution(CustomFunction& customfunction, int z) {
vector> ans;
for(int x = 1; x <= 1000; x++)
{
for(int y = 1; y <= 1000; y++)
{
if(customfunction.f(x, y) == z)
ans.push_back({x,y});
if(customfunction.f(x, y) > z)
break;
}
}
return ans;
}
}; 2. 循环码排列(Circular Permutation in Binary Representation)
题目链接
https://leetcode-cn.com/contest/weekly-contest-160/problems/circular-permutation-in-binary-representation/
题意
给你两个整数
n和start。你的任务是返回任意(0,1,2,,...,2^n-1)的排列p,并且满足:
p[0] = startp[i]和p[i+1]的二进制表示形式只有一位不同p[0]和p[2^n -1]的二进制表示形式也只有一位不同示例 1:
输入:n = 2, start = 3 输出:[3,2,0,1] 解释:这个排列的二进制表示是 (11,10,00,01) 所有的相邻元素都有一位是不同的,另一个有效的排列是 [3,1,0,2]示例 2:
输出:n = 3, start = 2 输出:[2,6,7,5,4,0,1,3] 解释:这个排列的二进制表示是 (010,110,111,101,100,000,001,011)提示:
1 <= n <= 160 <= start < 2^n
解题思路
相邻两二进制只有一位不同,同时头与尾两个数的二进制也只有一位不同。
因此,如果把头尾看成连起来的,那就是一个环,那么就是整个都是格雷码
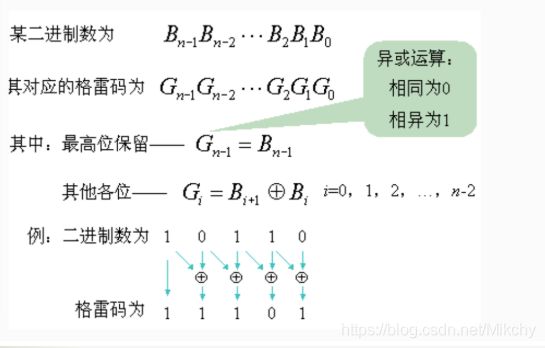
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。
格雷码的一个规则,利用异或来求
为了方便计算,如果是一个十进制数求其格雷码,如果要用上面那种规则来,我们就需要求出该十进制数的二进制表达
但是如果我们通过下面的规则:
1、把该十进制数 右移一位,即 x >> 1
2、把原来的数和 右移一位的数 直接异或,即可得到对应的格雷码相应的十进制数
原理还是和上面那个图一样,当我们 右移一位 之后,最高位变成0 ,0与任何数的异或还是本身,所以 最高位保留,同时因为右移一位,直接异或,就满足其他位是当前位和上一个位置的异或。
当我们得到了标准的格雷码序列的时候,剩下的就是找到起始数,也就是start,从该位存进答案,最后看成一个环,从该位存进,直到该位的上一位。
就得到最后要求的答案。
核心主要还是如何求,格雷码
AC代码(C++)
class Solution {
public:
vector circularPermutation(int n, int start) {
vector ans, arr;
int MAXN = 1<>1);
j = i ^ j;
arr.push_back(j);
}
int pos = -1;
for(int i = 0;i < MAXN;i++)
{
if(arr[i] == start) // 找到起始位后,开始存放
pos = i;
if(pos != -1)
ans.push_back(arr[i]);
}
// 最后把起始位前面那部分的格雷码也按顺序存进去
for(int i = 0;i < pos;i++)
ans.push_back(arr[i]);
return ans;
}
}; 3.串联字符串的最大长度(Maximum Length of A Concatenated String with Unique Characters)
题目链接
https://leetcode-cn.com/contest/weekly-contest-160/problems/maximum-length-of-a-concatenated-string-with-unique-characters/
题意
给定一个字符串数组
arr,字符串s是将arr某一子序列字符串连接所得的字符串,如果s中的每一个字符都只出现过一次,那么它就是一个可行解。请返回所有可行解
s中最长长度。示例 1:
输入:arr = ["un","iq","ue"] 输出:4 解释:所有可能的串联组合是 "","un","iq","ue","uniq" 和 "ique",最大长度为 4。示例 2:
输入:arr = ["cha","r","act","ers"] 输出:6 解释:可能的解答有 "chaers" 和 "acters"。示例 3:
输入:arr = ["abcdefghijklmnopqrstuvwxyz"] 输出:26提示:
1 <= arr.length <= 161 <= arr[i].length <= 26arr[i]中只含有小写英文字母
解题分析
根据字符串数组的长度,为16,每个字符串有两种情况,选或不选,所以一共有 2^16 种情况
所以可以考虑直接 DFS + 回溯
考虑每一个字符串,分两种情况:
1、主观上,我不选这个字符串,那就考虑下一个字符串
2、我考虑选这个字符串,但是这个字符串能不能选,要检查和前面有没有冲突(就是字母计数有没有重复)
如果没有重复,那就可以考虑选这个字符串,同时长度也增加了。不然不能选。
最后要把选的这个去掉,回溯。
最后就是在DFS前,要考虑长度如果比答案大,那就此时的长度为新答案
同时考虑的字符串已经超过字符串数组的大小了,那就说明没得考虑了,直接return
AC代码(C++)
class Solution {
public:
int ans;
int cnt[26];
void dfs(vector arr, int cur, int n, int len)
{
if(len > ans) ans = len;
if(cur >= n) return;
dfs(arr, cur+1, n, len);
for(auto c : arr[cur])
++cnt[c - 'a'];
bool flag = true;
for(int i = 0;i < 26;i++)
{
if(cnt[i] > 1)
{
flag = false;
break;
}
}
if(flag)
dfs(arr, cur+1, n, len+arr[cur].size());
for(auto c : arr[cur]) // 回溯
--cnt[c - 'a'];
}
int maxLength(vector& arr) {
memset(cnt, 0, sizeof(cnt));
ans = 0;
int n = arr.size();
dfs(arr, 0, n, 0);
return ans;
}
};
4.铺瓷砖(Tiling A Rectangle with the Fewest Squares)
题目链接
https://leetcode-cn.com/contest/weekly-contest-160/problems/tiling-a-rectangle-with-the-fewest-squares/
题意
你是一位施工队的工长,根据设计师的要求准备为一套设计风格独特的房子进行室内装修。
房子的客厅大小为
nxm,为保持极简的风格,需要使用尽可能少的 正方形 瓷砖来铺盖地面。假设正方形瓷砖的规格不限,边长都是整数。
请你帮设计师计算一下,最少需要用到多少块方形瓷砖?
示例 :有图示,具体点进链接查看
提示:
1 <= n <= 131 <= m <= 13
解题分析
困难题,有一些人就打表提交,有一些人暴力,有一些人是有原理的。
我给出两个链接
第一个链接,有具体讲解与代码实现
https://leetcode.com/problems/tiling-a-rectangle-with-the-fewest-squares/discuss/414260/8ms-Memorized-Backtrack-Solution-without-special-case!
第二个链接讲的是这个的内容和对应的参考文献可以借鉴。
https://leetcode-cn.com/problems/tiling-a-rectangle-with-the-fewest-squares/solution/guan-yu-ben-ti-shi-npwan-quan-wen-ti-de-zheng-ming/
(具体代码实现,我用的是打表,网上有所有情况的答案,剩下那就是记成一个 13*13 的二维数组即可,不过这个方法肯定没啥用,大家还是要弄明白原理才行,哈哈哈)
AC代码(C++)
class Solution {
public:
int tilingRectangle(int n, int m) {
if(n < m)
{
int temp = n;
n = m;
m = temp;
}
int res[13][13] = {
{1},
{2,1},
{3,3,1},
{4,2,4,1},
{5,4,4,5,1},
{6,3,2,3,5,1},
{7,5,5,5,5,5,1},
{8,4,5,2,5,4,7,1},
{9,6,3,6,6,3,6,7,1},
{10,5,6,4,2,4,6,5,6,1},
{11,7,6,6,6,6,6,6,7,6,1},
{12,6,4,3,6,2,6,3,4,5,7,1},
{13,8,7,7,6,6,6,6,7,7,6,7,1}
};
return res[n-1][m-1];
}
};