Trie树的双数组实现
本文原文链接:点击打开链接
正文组织
1.什么是Trie树?
2.如何实现一个Trie树?
3.三数组Trie(Tripple-Array Trie)
4.双数组Trie(Double-Array Trie)
5.后缀压缩
6.关键词插入操作
7.关键词删除操作
8.双输出池分配(Double-Array Pool Allocation)
9.实现DFA:Determine Finite Automatic,
10.下载
11.其他实现
12.参考文献
什么是Trie树?
Trie树是一种数字搜索树。(点击查看详细描述)[Fredkin1960]引进了trie这个术语,是“Retrieval”的简写,指检索之意。
如何实现一个Trie树?Trie树是一种有效的检索方式。事实上,它也是一种确定型有限自动机(DFA:Determine Finite Automatic,)。在Trie树中,每一个节点都对应一个状态,每一个标记的边都代表一个DFA中的而一个状态转移关系。对Trie树的遍历从根节点开始,当给定一个查询关键词时,每次消耗查询词的一个字母,下一个节点为于当前字母相同的边所指向的节点。当关键词的所有字母消耗完或者我们到了一个叶子节点,则整个检索过程结束。当我们走到一节点之后,发现该节点不存在于当前字母标记的边,或者当前节点为叶子节点,而关键词的字母尚未消耗完,则说明当前关键词在trie树中检索失败。
此处要注意的是,从trie树的根节点遍历到叶子节点所需的时间跟数据库的大小没有关系,而是与查询关键词的长度成正比的。所以,trie树的查询通常比B-树或者任何其他基于比较检索的方法要快很多。它的时间复杂度与hash方法是近似的。
除了检索效率高之外,trie树在关键词拼写错误的情况下也能够提供很好的方法来进行拼写的检查。例如,可以在检索过程中跳过一些字符便可以纠正插入类型的错误;可以通过在不消耗字符的情况下,遍历当前节点的所有子节点的方式便可以纠正删除类型的错误;甚至我们可以当当前节点不存在标记为当前字符的子节点时,直接跳过当前字符,然后进入当前节点的所有子节点来达到纠正插入类型错误。
三数组Trie树通常一个DFA有一张状态转移表来表示,转移表的行代表状态机的各个状态,列表示转换字符。转换表中第i行第j列的值表示在状态i的情况下输入字符j的时候的目标状态。
这种表示方式能够提供快速的遍历,以为每一个转移都可以有一个行号和列号进行索引。然而在空间上,这种表示形式则存在很大的浪费,因为对于trie树,大多数的节点都只有少数的几个分支,这边使得转移表中的大量的空间浪费了。
相对于转移表表示方式,可以利用链表的形式来存储每个状态的状态转移关系。但是由于链表是一个线性访问结构,从而导致了trie树的检索效率下降。
为了保证trie树的访问效率和空间的不浪费,便有人提出了对转移表进行压缩的方法来实现trie树。
1.[Johnson1975]利用4个数组来表示DFA,在trie树的情况下可以精简到3个数组。这种方式下,状态转移表的行时以重叠的方式分配的,这样使得那些空闲的单元能够被其他的状态利用。
2.[Aoe1989]提出了对3个数组的表示方式的一种改进,使得之用两个数组即可
双数组Trie树正如 [Aho+1985] page 144-146中所讲到的,DFA压缩表示可以通过四个数组来表示,即default,base,next以及checkt四个数组。然而由于仅用于信息检索的trie树比此法分析要简单许多,所以default数组其实可以省略。因此一个trie树能够利用三个数组来实现。
结构
三数组(tripple-array)结构有以下三个数组组成:
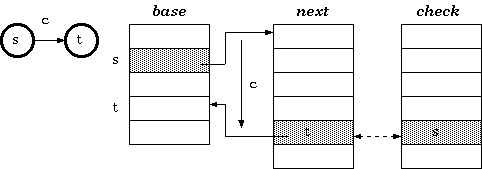
1.base数组:base数组的每一个元素都对应trie树中的一个节点。对于trie树中的一个节点s,node[s]表示该节点在数组next和check数组中的起始索引,该索引表示节点s在状态转移表中的行号。
2.next数组:这个数组与check数组协同工作。它提供给一个缓冲池以供trie树的状态转移表的行所代表的的稀疏向量的空间分配。即,trie树中的每一个节点的状态转移向量都会存储于next数组中
3.check数组:这个数组与next数组协同工作。它用于标记next数组中的元素所属的trie树节点。这样便允许相邻的两个空间分配给不同的节点。
定义1:假设状态s下,输入字符为c时的目标状态为t,那么会有check[base[s] + c] = s, next[base[s] + c] = t.该关系可以用下图表示:
遍历
根据定义1,在给定状态s的情况下,输入字符为c,则下一个状态通过如下方式获取:
构造方式t := base[s] + c; if check[t] = s then next state := next[t] else fail endif
为了插入状态s的一个新的转移,比如输入字符为c则转移到状态t,那么要求next[base[s] + c]这个地址单元必须可用。如果该地址单元是空的,那我们可以直接插入;否则的话要么需要移动当前单元格所有的节点或者节点s的转移向量需要重新调整位置。实际中根据调整二者的代价来决定重新调整哪个节点的转移向量。在找到了空闲的地址单元来存储转移向量之后,转移向量必须按照如下的方式进行重新计算。假设新的存放地址从b开始,则重新分配的过程如下所示:Procedure Relocate(s : state; b : base_index) { Move base for state s to a new place beginning at b } begin foreach input character c for the state s { i.e. foreach c such that check[base[s] + c]] = s } begin check[b + c] := s; { mark owner } next[b + c] := next[base[s] + c]; { copy data } check[base[s] + c] := none { free the cell } end; base[s] := b end

利用三数组结构实现trie树似乎已经足够好了,但是这种方式在实际中无法保存在一个单一的文件中(原句:The tripple-array structure for implementing trie appears to be well defined,but is still not practical to keep in a single file.这句觉得翻译的不准确)。事实上next/check两个数组可以以整数对的形式存储于一个数组中,但是由于base数组并不会随着next/check的增长而增长的,所以通常将base数组单独分开。
为了解决这个问题,[Aoe1989]将数组个数减少到了两个。在双数组结构中,base数组和next数组合并为一个数组,从而该结构中只有两个平行的数组,即base和check数组。
结构
在双数组Trie树中,数组中的trie树节点是直接在base数组和check数组之间进行连接的,而不像三数组的表示中的那样通过状态号进行连接。
定义2:对于状态s,如果输入字符为c,则目标转移状态为t的这个转移关系来说,base数组和check数组会有如下关系:check[base[s] + c] = s, base[s] + c = t.如下图所示:
遍历
根据定义2,当给定状态c和输入字符c,则下一个状态由以下方式确定:
t := base[s] + c;if check[t] = s thennext state := telsefail构造endif双数组trie数的构建与三数组trie树的构建基本类似,不同点在于base数组中空间分配:
Procedure Relocate(s : state; b : base_index){ Move base for state s to a new place beginning at b }begin
foreach input character c for the state s{ i.e. foreach c such that check[base[s] + c]] = s }begin
check[b + c] := s; { mark owner }
base[b + c] := base[base[s] + c]; { copy data }
{ the node base[s] + c is to be moved to b + c;
Hence, for any i for which check[i] = base[s] + c, update check[i] to b + c }
foreach input character d for the node base[s] + c
begin
check[base[base[s] + c] + d] := b + c
end;
check[base[s] + c] := none { free the cell }end;
base[s] := b
后缀压缩end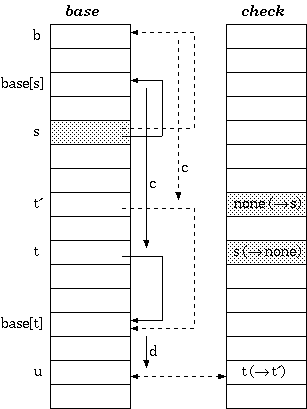
[Aoe1989]在此基础上还提出了一种存储压缩的策略,这种策略通过将没有分支的后缀存储于一个字符串中,称之为tail。这样一来,那些没有分支的节点访问便简化为字符串的比较问题了。
由于双数组和后缀压缩是两个完全不同的数据结构,因此关键词的插入和删除算法必须根据这两个数据结构的特性做相应的调整。
关键词插入
(未完待续)