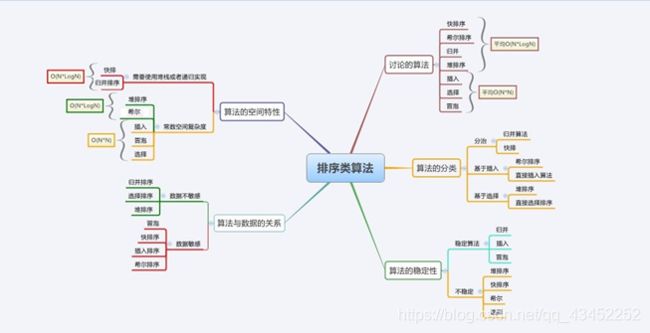
Java中七大基于比较的排序算法
目录
- 插入排序
-
- 直接插入排序
-
- 基本原理
- 代码实现
- 性能分析
- 折半插入排序
-
- 代码实现
- 希尔排序
-
-
- 基本原理
- 代码实现
- 性能分析
-
- 选择排序
-
- 单向选择排序
-
- 基本原理
- 代码实现
- 性能分析
- 双向选择排序
-
- 代码实现
- 堆排序
-
-
- 基本原理
- 代码实现
- 性能分析
-
- 冒泡排序
-
-
- 基本原理
- 代码实现
- 性能分析
-
- 快速排序
-
-
- 基本原理
- 代码实现(递归和非递归)
- 性能分析
-
- 归并排序
-
-
- 基本原理
- 代码实现
- 性能分析
-
- 排序总结
-
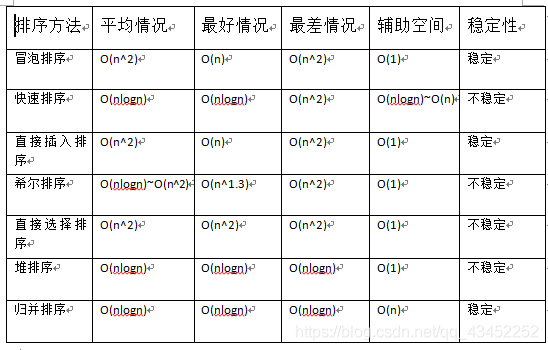
- 各种排序算法之间的比较
插入排序
直接插入排序
基本原理
整个区间分为两部分:有序区间和无序区间,每次选择无序区间的第一个元素,选择有序区间内合适的位置插入

代码实现
public static void insertSort(int[] array){
for(int i = 1; i < array.length; i++){
int key = array[i];
int end = i - 1;
while(end >= 0 && key < array[end]){
array[end + 1] = array[end];
end--;
}
array[end + 1] = key;
}
}
性能分析
稳定性:稳定
时间复杂度:O(N2)
空间复杂度:O(1)
应用场景:序列接近有序或者数据个数比较少
折半插入排序
代码实现
public static void insertSort1(int[] array){
for(int i = 1; i < array.length; i++){
int key = array[i];
int left = 0;
int right = i;
while(left < right){
int mid = (left + right) / 2;
if(key >= array[mid]){
left = mid + 1;
}else{
right = mid;
}
}
for(int j = i; j > left; j--){
array[j] = array[j-1];
}
array[left] = key;
}
}
希尔排序
基本原理
希尔排序是对直接插入排序的优化,将数组先分割成组,直到数组接近有序,最后再进行插入排序时就不用移动那么多位置了
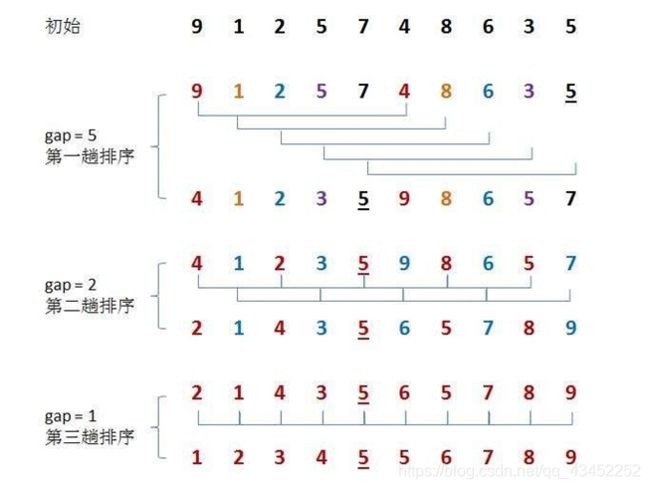
代码实现
public static void shellSort(int[] array){
int gap = array.length;
while(gap > 1){
gap = gap/3 + 1;
for(int i = gap; i < array.length; i++){
int end = i - gap;
int key = array[i];
while(end >= 0 && key < array[end]){
array[end+gap] = array[end];
end -= gap;
}
array[end+gap] = key;
}
gap--;
}
}
性能分析
稳定性:不稳定
时间复杂度:O(N2)
空间复杂度:O(1)
选择排序
单向选择排序
基本原理
每次从无序区间内选出最大(或最小)的一个元素,存放在无序区间的最后(或最前)位置,直到全部待排序的元素排完
代码实现
//交换数组元素
private static void swap(int[]array,int parent,int child){
int temp = array[parent];
array[parent] = array[child];
array[child] = temp;
}
//只能找出最大的元素
public static void selectSort(int[] array){
for(int i = 0; i < array.length - 1; ++i){
int maxPos = 0;
for(int j = 1; j < array.length - i; ++j){
if(array[j] > array[maxPos]){
maxPos = j;
}
}
if(maxPos != array.length - 1 - i){
swap(array, maxPos, array.length - 1 - i);
}
}
}
性能分析
稳定性:不稳定
时间复杂度:O(N2)
空间复杂度:O(1)
应用场景:数据不敏感
双向选择排序
代码实现
//同时找出最大和最小的元素(优化)
public static void selectSortOP(int[] array){
int begin = 0;
int end = array.length - 1;
while(begin < end){
int maxPos = begin;
int minPos = begin;
int index = begin + 1;
while(index <= end){
if(array[index] > array[maxPos]){
maxPos = index;
}
if(array[index] < array[minPos]){
minPos = index;
}
++index;
}
//将最大元素放在区间最后一个位置
if(maxPos != end){
swap(array, maxPos, end);
}
//如果最小元素刚好在区间最后一个位置,必须要更新minPos
if(minPos == end){
minPos = maxPos;
}
if(minPos != begin){
swap(array,minPos,begin);//交换方法见单向选择排序
}
begin++;
end--;
}
}
堆排序
基本原理
堆排序使用到了完全二叉树的一个特性,根节点比左孩子和右孩子都要大,完成一次建堆的操作实质上是比较根节点和左孩子、右孩子的大小,大的交换到根节点上,直至最大的节点在树顶,然后与数组的最后一位元素进行交换

代码实现
public static void shiftDown(int[]array,int parent,int size){
int child = parent*2+1;
while(child < size){
//找左右孩子中较大的孩子
if(child+1<size && array[child+1]>array[child]){
child += 1;
}
if(array[child] > array[parent]){
swap(array,child,parent);
parent = child;
child = parent * 2 + 1;
}else
{
return;
}
}
}
//堆排序
public static void heapSort(int[]array){
//1.建堆
//找倒数第一个非叶子节点
int lastLeaf = (array.length - 2)>>1;
//从lastLeaf到root位置不断向下调整
for(int root = lastLeaf;root >= 0;root--){
shiftDown(array,root,array.length);
}
//2.利用对删除的思想进行排序
int end = array.length -1;
while(end >= 0){
swap(array,0,end);
shiftDown(array,0,end);
end--;
}
}
性能分析
稳定性:不稳定
时间复杂度:O(N*logN)
空间复杂度:O(1)
冒泡排序
基本原理
在无序区间,通过相邻数的比较,将最大的数冒泡到无序区间的最后,重复这个过程,直到数组整体有序

代码实现
public static void bubbleSort(int[] array){
boolean isChange = false;
//控制排序的趟数
for(int i = 0; i < array.length; i++){
//控制当前趟数需要比较的次数
for(int j = 1; j < array.length - i; j++){
if(array[j] < array[j - 1]){
swap(array, j, j-1);
isChange = true;
}
}
if(isChange == false){
break;
}
}
}
性能分析
稳定性:稳定
时间复杂度:O(N2)
空间复杂度:O(1)
快速排序
基本原理
- 从区间中取一个数作为基准值,按照该基准值将区间划分为左右两部分;
- 按照快排的思想排左部分;
- 按照快排的思想排右部分。
三种划分方式 - horen分割
public static int partion1(int[]array,int left,int right){
int begin = left;
int end = right - 1;
int key = array[end];
while(begin < end){
//begin从前往后找,比基准值大的元素
while(begin < end && array[begin] <= key){
begin++;
}
//end从后往前找,比基准值小的元素
while(end >= 0 && array[end] >= key){
end--;
}
if(begin < end){
swap(array,begin,end);
}
}
if(begin != right - 1){
swap(array,begin,right-1);
}
return begin;
}
- 挖坑法
public static int partion2(int[]array,int left,int right){
int begin = left;
int end = right - 1;
int key = array[end];
while(begin < end){
//begin从前往后找,比基准值大的元素
while(begin < end && array[begin] <= key){
begin++;
}
//找到了比基准值大的元素,用begin填坑
if(begin < end){
array[end] = array[begin];
end--;
}
//end从后往前找,比基准值小的元素
while(end >= 0 && array[end] >= key){
end--;
}
//找到了一个比基准值小的元素,用end来填坑
if(begin < end){
array[begin] = array[end];
begin++;
}
}
//用key值来填最后一个坑
array[begin] = key;
return begin;
}
- 前后指针法
public static int partion3(int[] array,int left,int right){
int cur = left;
int prev = cur - 1;
int key = array[right-1];
while(cur < right){
if(array[cur] < key && ++prev != cur){
swap(array, cur, prev);
}
++cur;
}
if(++prev != right - 1){
swap(array, prev,right-1);
}
return prev;
}
代码实现(递归和非递归)
递归
//取基准值的优化
public static int getIndexOfMiddle(int[]array, int left, int right)
{
int mid = left + ((right - left) >> 1);
if(array[left] < array[right-1])
{
if(array[mid] < array[left])
{
return left;
}
else if(array[mid] > array[right-1])
{
return right - 1;
}
else
{
return mid;
}
}
else{
if(array[mid] > array[left])
{
return left;
} else if (array[mid] < array[right-1])
{
return right - 1;
}
else
{
return mid;
}
}
}
public static void quickSort(int[]array,int left,int right){
if(right - left < 16){
insertSort(array, left, right);
}else{
//说明区间至少有两个元素
int div = partion3(array,left,right);
//快排基准值的左侧
quickSort(array, left, div);
quickSort(array,div + 1, right);
}
}
非递归
public static void quickSortNor(int[] array){
Stack<Integer> s = new Stack<>();
s.push(array.length);
s.push(0);
while(!s.isEmpty()){
int left = s.pop();
int right = s.pop();
if(right - left > 1){
int div = partion1(array, left, right);
s.push(right);
s.push(div+1);
s.push(div);
s.push(left);
}
}
}
性能分析
稳定性:不稳定
时间复杂度:O(NlogN)
空间复杂度:O(logN)
应用场景:数据量大比较随机
归并排序
基本原理
采用分治法,将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。不断进行拆分合并,直到完全有序。
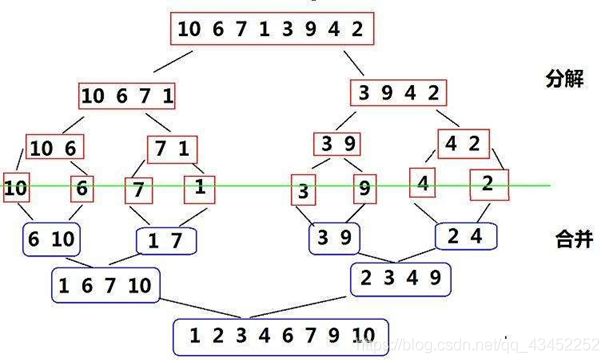
代码实现
递归
public static void mergeData(int[] array, int left, int mid, int right, int[] temp){
int index = left;
int begin1 = left, end1 = mid, begin2 = mid, end2 = right;
while(begin1 < end1 && begin2 < end2){
if(array[begin1] <= array[begin2]){
temp[index++] = array[begin1++];
}
else{
temp[index++] = array[begin2++];
}
}
//第一个区间还有数据
while(begin1 < end1){
temp[index++] = array[begin1++];
}
//第二个区间有数据
while(begin2 < end2){
temp[index++] = array[begin2++];
}
}
public static void mergeSort(int[] array, int left, int right, int[] temp){
if(right - left > 1){
int mid = left + ((right - left) >> 1);
//左半部分[left,mid)
mergeSort(array, left, mid, temp);
//右半部分
mergeSort(array, mid, right, temp);
//归并
mergeData(array, left, mid, right, temp);
//归并结束后,有序数列在temp中
//将temp中的数据拷贝到array中
System.arraycopy(temp, left, array, left, right-left);
}
}
public static void mergeSort(int[] array){
int[] temp = new int[array.length];
mergeSort(array, 0, array.length, temp);
}
非递归
public static void mergeSortNor(int[] array){
int[] temp = new int[array.length];
int gap = 1;
while(gap < array.length){
for(int i = 0; i < array.length; i += gap*2){
int left = i;
int mid = left + gap;
int right = mid + gap;
if(mid > array.length){
mid = array.length;
}
if(right > array.length){
right = array.length;
}
mergeData(array, left, mid, right, temp);
}
System.arraycopy(temp, 0, array, 0, array.length);
gap <<= 1;
}
}
性能分析
稳定性:稳定
时间复杂度:O(N*logN)
空间复杂度:O(N)