Leetcode进阶之路——Trie(Prefix Tree)

关于前缀树的介绍网上已有很多文章，简单的说，这是一种典型的“空间换时间”的数据结构
前缀树可构造如下：

class TrieNode
{
	int val;
	TrieNode* children[num];
	bool flag;
public:
	TrieNode()
	{
		val = 0;
		memset(children, 0, sizeof(children));
		flag = false;
	}
	TrieNode(int x)
	{
		val = x;
		memset(children, 0, sizeof(children));
		flag = false;
	}
};

class Trie
{
	TrieNode* root;
public:
	Trie()
	{
		root = new TrieNode();
	}
};

解释一下，我们平时见到的Trie树一般如下（图摘自网络）：

　　这整一棵树是Trie，而树中的每个节点则是TrieNode
　　最顶端的是root节点，该节点为空，之后的每个节点均包含三个属性：
val：节点的值
children[]：指向子节点的指针，children的大小根据实际需求来定。例如如果我们要存的是单词，那么单词数最多只有26个，则设为children[26]即可，如果是数字，则设为children[10]，并不固定
flag：标志位，该属性后面会用到，不同场景下表示的意义不同。
　　接下来以一个实例来直观感受前缀树的创建过程：
　　比如有"abcd" 和 “abba"两个字符串，由于是英文字母，则可以假设children大小为26
　　首先进来"abcd”，第一个字符是’a’，root这时候是空的，它指向a子节点也是空的，于是初始化其a子节点，同时使当前指针指向a子节点，依次循环，直到遍历完字符串，整个流程如下

注意，前面"a"、“ab”、"abc"的flag均为false，表示这些字符串并没有单独出现，只是完整字符串的一部分，只有当遍历完，"abcd"的d节点的flag才是true
　　这样第一个字符串结束，进来第二个abba，同样从root节点开始，第一个字符是’a’，root的’a’子节点有数值，则不操作，直接将当前指针指向a子节点，第二个是b，同样不为空，继续指向b子节点，第三个b为空，则新建，直到第四个a，遍历结束，同时设置其flag为true

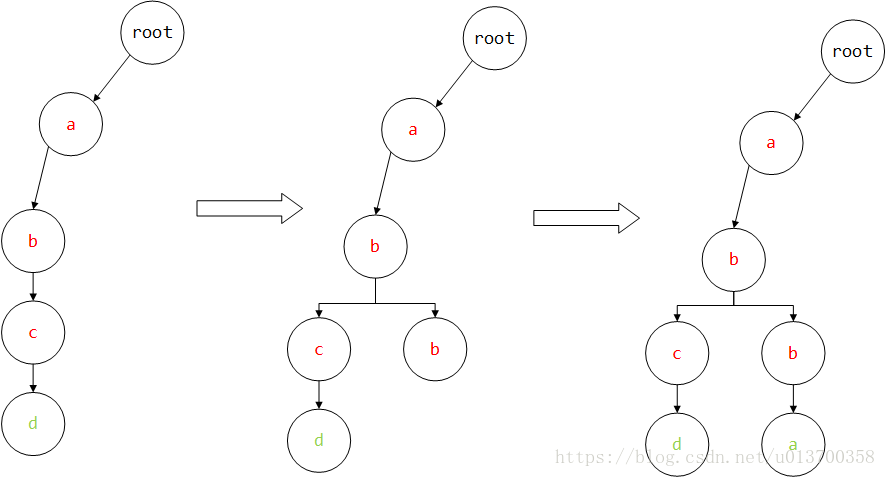
代码实现如下：

	void insert(string word)
	{
		TrieNode* tn = root;
		//遍历整个字符串
		for (int i = 0; i < word.length(); ++i)
		{
			//取出当前字符
			char c = word[i];
			//若子节点为空，则新建节点，否则直接另其指向子节点
			if (tn->children[c - 'a'] == NULL)
			{
				tn->children[c - 'a'] = new TrieNode(c);
			}
			tn = tn->children[c - 'a'];
		}
		//遍历完后，令当前节点的标记为为true，默认均为false
		tn->flag = true;
	}

上述为构造的过程，怎么查找呢？也很简单，比如这时来了一个"ab"字符串，同样从root开始查找，发现a子节点有值，则另其指向a节点，a节点的b子节点也有值，继续往下，然而此时目标字符串已经遍历完结，但当前b节点的flag标记为false，则表示"ab"字符串并未在原字符串数组中出现，返回false
　　来看一道leetcode上经典前缀树的例题：
　　208. Implement Trie (Prefix Tree)

Implement a trie with insert, search, and startsWith methods.
Example:
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // returns true
trie.search(“app”); // returns false
trie.startsWith(“app”); // returns true
trie.insert(“app”);
trie.search(“app”); // returns true

insert是插入新字符串
search是判断所给字符串是否在之前出现过
startswith则是判断是否有以当前字符串开头的字符串
直接给出我的AC代码：

class TrieNode {
public:
	char val;
	bool exist;
	TrieNode* children[26];
public:
	TrieNode()
	{
		val = 0, exist = false;
		memset(children, 0, sizeof(children));
	}
	TrieNode(char c)
	{
		val = c;
		exist = false;
		memset(children, 0, sizeof(children));
	}
};

class Trie {
	TrieNode* root;
public:
	/** Initialize your data structure here. */
	Trie() {
	        root = new TrieNode();
	}

	/** Inserts a word into the trie. */
	void insert(string word) {
		TrieNode* tn = root;
		for (int i = 0; i < word.length(); ++i)
		{
			char c = word[i];
			if (tn->children[c - 'a'] == NULL)
			{
				tn->children[c - 'a'] = new TrieNode(c);
			}
			//if (i == word.length() - 1)
				//tn->exist = true;
			tn = tn->children[c - 'a'];
		}
	        tn->exist = true;
	}

	/** Returns if the word is in the trie. */
	bool search(string word) {
		TrieNode* tn = root;
	        if(word.length() <= 0) return true;
		for (int i = 0; i < word.length(); ++i)
		{
			char c = word[i];
			if (tn == NULL || tn->children[c - 'a'] == NULL)
				return false;
			//if (i == word.length() - 1 && tn->exist == false)
				//return false;
			tn = tn->children[c - 'a'];
		}
		return tn->exist;
	}

	/** Returns if there is any word in the trie that starts with the given prefix. */
	bool startsWith(string prefix) {
	        if(prefix.length() <= 0) return true;
		TrieNode* tn = root;
		for (int i = 0; i < prefix.length(); ++i)
		{
			char c = prefix[i];
			if (tn == NULL || tn->children[c - 'a'] == NULL)
				return false;
			tn = tn->children[c - 'a'];
			/*if (i == prefix.length() - 1 && tn->exist == false)
				return false;*/
		}
		return true;
	}
};

startswith和search的区别在于，后者必须是完整的匹配，因此要识别exist标记，而后者只要遍历完均存在于树中即可，因此最后直接返回true，前者的要求更低。

第二题：212. Word Search II

Given a 2D board and a list of words from the dictionary, find all words in the board.
Each word must be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example:
Input:
words = [“oath”,“pea”,“eat”,“rain”] and board =
[
[‘o’,‘a’,‘a’,‘n’],
[‘e’,‘t’,‘a’,‘e’],
[‘i’,‘h’,‘k’,‘r’],
[‘i’,‘f’,‘l’,‘v’]
]
Output: [“eat”,“oath”]

在做这题之前，可以先看一下79. Word Search
这道题一开始我直接用DFS遍历，也能通过，后来也试了下Trie，都OK
而第212题直接用DFS暴力搜索会超时，因此同样用Trie来构造字典树，代码如下：

//表示上下左右四个相邻方向
int dx[4] = { 0, 0, 1, -1 };
int dy[4] = { 1, -1, 0, 0 };
class TrieNode
{
public:
    TrieNode* children[26];
    char val;
    bool exist;
    TrieNode()
    {
        val = 0;
        exist = false;
        memset(children, 0, sizeof(children));
    }
    TrieNode(char c)
    {
        val = c;
        exist = false;
        memset(children, 0, sizeof(children));
    }
};

class Trie
{
public:
    TrieNode* root;
public:
    Trie()
    {
        root = new TrieNode();
    }
    //这里的搜索部分用DFS代替，因此只要insert函数
	void insert(string word)
	{
		TrieNode* tn = root;
		for (int i = 0; i < word.length(); ++i)
		{
			char c = word[i];
			if (tn->children[c - 'a'] == NULL)
			{
				tn->children[c - 'a'] = new TrieNode(c);
			}
			tn = tn->children[c - 'a'];
		}
		tn->exist = true;
	}
};


class Solution {
public:
	void dfs(vector> board, int i, int j, TrieNode* tn, string word, vector& res)
	{
		char c = board[i][j];
	    if(c == ' ') return;
	    //剪枝，如果当前的子节点已经是空的了，说明这之后的字符串一定没出现过，直接return
		if (tn->children[c - 'a'] == NULL) return ;
		if (tn->children[c - 'a']->exist == true)
		{
			//重复字符串
			if (find(res.begin(), res.end(), word + c) == res.end())
				res.emplace_back(word + c);
		}
		//直接置当前字符为空格，后面再恢复即可，这样就不需要维护visit数组
		board[i][j] = ' ';
		for (int k = 0; k < 4; ++k)
		{
			int xx = i + dx[k], yy = j + dy[k];

			if (xx >= board.size() || yy >= board[0].size() || xx < 0 || yy < 0)
				continue;
			dfs(board, xx, yy, tn->children[c - 'a'], word + c, res);
		}
		//恢复字符数组
		board[i][j] = c;
	}

	vector findWords(vector>& board, vector& words) {
		Trie t;
		for (int i = 0; i < words.size(); ++i)
			t.insert(words[i]);
		vector res;
		string str = "";
		for (int i = 0; i < board.size(); ++i)
		{
			str = "";
			for (int j = 0; j < board[0].size(); ++j)
			{
				dfs(board, i, j, t.root, "", res);
			}
		}
		sort(res.begin(), res.end());
		return res;
	}
};