LeetCode Weekly Contest 30解题思路
LeetCode Weekly Contest 30解题思路
详细代码可以fork下Github上leetcode项目,不定期更新。
赛题
本次周赛主要分为以下4道题:
- 566 Reshape the Matrix (3分)
- 560 Subarray Sum Equals K (6分)
- 567 Permutation in String (7分)
- 568 Maximum Vacation Days (9分)
566. Reshape the Matrix
Problem:
In MATLAB, there is a very useful function called ‘reshape’, which can reshape a matrix into a new one with different size but keep its original data.
You’re given a matrix represented by a two-dimensional array, and two positive integers r and c representing the row number and column number of the wanted reshaped matrix, respectively.
The reshaped matrix need to be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the ‘reshape’ operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
Example 1:
Input:
nums =
[[1,2],
[3,4]]
r = 1, c = 4
Output:
[[1,2,3,4]]
Explanation:
The row-traversing of nums is [1,2,3,4]. The new reshaped matrix is a 1 * 4 matrix, fill it row by row by using the previous list.
Example 2:
Input:
nums =
[[1,2],
[3,4]]
r = 2, c = 4
Output:
[[1,2],
[3,4]]
Explanation:
There is no way to reshape a 2 * 2 matrix to a 2 * 4 matrix. So output the original matrix.
Note:
- The height and width of the given matrix is in range [1, 100].
- The given r and c are all positive.
水题,不需要思考,时间复杂度为 O(n) ,代码如下:
public int[][] matrixReshape(int[][] nums, int r, int c) {
int row = nums.length;
if (row == 0) return nums;
int col = nums[0].length;
if (col == 0) return nums;
if (row * col != r * c) return nums;
int[][] res = new int[r][c];
for (int i = 0; i < row; i++){
for (int j =0; j < col; j++){
int x = i * col + j;
int nr = x / c;
int nc = x % c;
res[nr][nc] = nums[i][j];
}
}
return res;
}560. Subarray Sum Equals K
Problem:
Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.
Example 1:
Input:nums = [1,1,1], k = 2
Output: 2
Note:
- The length of the array is in range [1, 20,000].
- The range of numbers in the array is [-1000, 1000] and the range of the integer k is [-1e7, 1e7].
这道题虽然通过了,但对自己的AC答案非常不满意,它的时间复杂度为 O(n2) ,代码如下:
public int subarraySum(int[] nums, int k) {
if (nums.length == 0)
return 0;
int n = nums.length;
int[] sums = new int[n + 1];
sums[0] = 0;
for (int i = 1; i < sums.length; i++) {
sums[i] += sums[i - 1] + nums[i - 1];
}
int count = 0;
for (int i = 0; i < sums.length; i++) {
int target = sums[i] + k;
for (int j = i + 1; j < sums.length; j++) {
if (target == sums[j]) {
count++;
}
}
}
return count;
}累加和体现了子数组的连续性,那么该问题就转化成了目标的搜索问题。上述还有一种更加直观的解法,遍历每种可能长度的子序列,子序列最小长度为1,最大长度为当前数组,所以i = 1 to n,n为数组的长度,代码如下:
public int subarraySum(int[] nums, int k) {
int n = nums.length;
if (n == 0) return 0;
int[] sums = new int[n+1];
sums[0] = 0;
for (int i = 0; i < nums.length;i++){
sums[i+1] = nums[i] + sums[i];
}
int count = 0;
for (int i = 1; i <= n;i++){
for (int j = 0; j + i - 1 < n; j++){
int sum = sums[j+i]- sums[j];
if (sum == k) count++;
}
}
return count;
}累加和避免了多次计算,依然能够AC。但该代码的核心思想【暴力遍历】还是没有转变,它还有更好的解法么?
该问题的特殊性在于连续子数组,这让我想到了累加的特殊性。我们可以观察一下sums的生成过程,它从下标0慢慢累加到数组底端,这有个什么好处呢?我们可以想象一下木板的拼接和切割过程,nums[i]>0的数可表示拼接的长度,而nums[i] < 0的数可以表示切割的长度,题目是说找一个k,使得连续的nums[i] + ...+nums[j] == k,也就是说中间j-i+1的长度不定,回忆下刚才的解法,我们假定我们知道了长度,这意味着长度得从1 to n开始遍历。但这问题不能反过来思考么?
当我们拿到所有信息后,即全部的拼接和切割完成后,它们一定会留下深刻的痕迹,现在我们假设遍历完所有数组后木板的长度为sum,那么回过头来就得找sum-k的那部分长度是否有拼接和切割的痕迹,如果有,则说明它们一定可以从该点不断累加数组得到连续的k。
所以该题的思想出来了,我们并不知道k组成的连续操作长度是多少,我们也无需知道,而是记录每个操作完成后的位置(痕迹),如果当前的每个sum-k能够被找到,就进行计数。
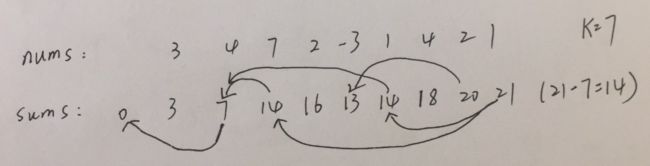
举个深刻的例子,来帮助理解。
nums = [0,3,4,7,2,-3,1,4,2,1] k = 7
sums = [0,3,7,14,16,13,14,18,20,21]我们来看看21这个痕迹点,21-7表示去搜寻14位置处是否有痕迹,而此时我们发现有两处痕迹能最终达到21,所以此处要让计数器+2。所以说,这个问题我们用 O(n) 就能解决了!
核心思想:把每个操作看成一个分割点,我们只需记录每个分割点的位置即可。因为它们必须是一系列连续的操作,所以我们可以按顺序遍历数组(并不影响最后的结果),其次在切割和拼接过程当中,拿一个容器记录痕迹出现的次数(map),当遇到新阶段后,只需要找寻new sum - k的痕迹即可,此处k中的长度不定,这是关键。所以代码如下:
public int subarraySum(int[] nums, int k) {
Map map = new HashMap<>();
map.put(0, 1);
int sum = 0;
int res = 0;
for (int num : nums){
sum += num;
if (map.containsKey(sum-k)){
res += map.get(sum-k); //搜寻指定痕迹
}
map.put(sum, map.getOrDefault(sum, 0)+1); //记录每个拼接或切割痕迹
}
return res;
} 非要拿物理解决方案去拟合代码还是很牵强,或许我们压根不会想的那么复杂,那么应该怎么去优化代码呢?再来看第一种方案的代码,它其实离正确的解决方案不远了。观察它的结构,
int count = 0;
for (int i = 0; i < sums.length; i++) {
int target = sums[i] + k;
for (int j = i + 1; j < sums.length; j++) {
if (target == sums[j]) {
count++;
}
}
}这部分非常有趣,我们为了搜索target需要遍历当前i的后i+1起的元素,并记录出现次数。既然我们能够遍历一次i后的所有元素,我们不能把第一次遍历后的信息记录下来?为什么不行呢?
在这里我们肯定不能这么做,因为有一个条件限制住了我们,你如果记录了i+1后的所有元素次数,那就意味着再求target = sums[i+3]+k的时候,你就无形利用了之前i+1后所记录的信息,而在求此target时,应该利用i+4后所记录的信息。
这个问题还是得逆向思考,如上图所展示的那样,此思路明显得把可能组成k的长度都遍历一遍,所以它的思维过程是这样的。
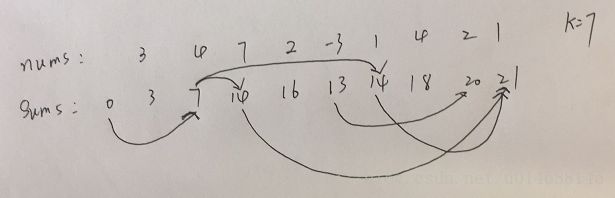
此题的解法如上,它搜索解的方向性给了我们一个启发,因为它总是向后搜索,所以我们完全可以让所有的剪头反向,这一操作不会影响我们最终的答案。一反向,呵呵,就把之前要 O(n2) 的操作变成了 O(n) ,谁叫它的搜索只要求向后呢,一目了然。
567. Permutation in String
Problem:
Given two strings s1 and s2, write a function to return true if s2 contains the permutation of s1. In other words, one of the first string’s permutations is the substring of the second string.
Example 1:
Input:s1 = “ab” s2 = “eidbaooo”
Output:True
Explanation: s2 contains one permutation of s1 (“ba”).
Example 2:
Input:s1= “ab” s2 = “eidboaoo”
Output: False
Note:
- The input strings only contain lower case letters.
- The length of both given strings is in range [1, 10,000].
水题,思路很简单,不考虑顺序,那么用map记录出现次数即可。最简单的做法,遍历s2中的所有长度可能为s1.length的子串,分别统计字符出现的次数,如果相等返回true,否则返回false。代码如下:
public boolean checkInclusion(String s1, String s2) {
int[] map1 = new int[26];
for (int i = 0; i < s1.length(); i++){
map1[s1.charAt(i)-'a']++;
}
int len = s1.length();
for (int i = 0; i + len -1 < s2.length(); i++) {
String tmp = s2.substring(i, i+len);
int[] map2 = new int[26];
for (int j = 0; j < tmp.length();j++){
map2[tmp.charAt(j)-'a']++;
}
if (isArraySame(map1, map2)) return true;
}
return false;
}
private boolean isArraySame(int[] map1, int[] map2){
for (int i = 0; i < map1.length; i++){
if (map1[i] != map2[i]) return false;
}
return true;
}这代码速度相当的慢,因为我遍历了每种可能的子数组,咋说呢,就是在滑动的时候并没有把滑动窗口重叠的部分给记录下来,而是直接忽略了这些状态,所以如果窗口比较大那么开销就非常严重。所以优化思路就是把滑动窗口重叠的那一部分信息给利用起来。
public boolean checkInclusion(String s1, String s2) {
int n = s1.length();
int m = s2.length();
if (n > m)
return false;
int[] f = new int[26];
for (int i = 0; i < n; i++) {
f[s1.charAt(i) - 'a']++;
}
int[] g = new int[26];
for (int i = 0; i < n; i++) {
g[s2.charAt(i) - 'a']++;
}
if (isArraySame(f, g))
return true;
for (int i = 1; i + n - 1 < s2.length(); i++) {
g[s2.charAt(i - 1) - 'a']--;
g[s2.charAt(i + n - 1) - 'a']++;
if (isArraySame(f, g))
return true;
}
return false;
}
private boolean isArraySame(int[] map1, int[] map2) {
for (int i = 0; i < map1.length; i++) {
if (map1[i] != map2[i])
return false;
}
return true;
}568. Maximum Vacation Days
Problem:
LeetCode wants to give one of its best employees the option to travel among N cities to collect algorithm problems. But all work and no play makes Jack a dull boy, you could take vacations in some particular cities and weeks. Your job is to schedule the traveling to maximize the number of vacation days you could take, but there are certain rules and restrictions you need to follow.
Rules and restrictions:
- You can only travel among N cities, represented by indexes from 0 to N-1. Initially, you are in the city indexed 0 on Monday.
- The cities are connected by flights. The flights are represented as a N*N matrix (not necessary symmetrical), called flights representing the airline status from the city i to the city j. If there is no flight from the city i to the city j, flights[i][j] = 0; Otherwise, flights[i][j] = 1. Also, flights[i][i] = 0 for all i.
- You totally have K weeks (each week has 7 days) to travel. You can only take flights at most once per day and can only take flights on each week’s Monday morning. Since flight time is so short, we don’t consider the impact of flight time.
- For each city, you can only have restricted vacation days in different weeks, given an N*K matrix called days representing this relationship. For the value of days[i][j], it represents the maximum days you could take vacation in the city i in the week j.
You’re given the flights matrix and days matrix, and you need to output the maximum vacation days you could take during K weeks.
Example 1:
Input:flights = [[0,1,1],[1,0,1],[1,1,0]], days = [[1,3,1],[6,0,3],[3,3,3]]
Output: 12
Explanation:
Ans = 6 + 3 + 3 = 12.One of the best strategies is:
1st week : fly from city 0 to city 1 on Monday, and play 6 days and work 1 day.
(Although you start at city 0, we could also fly to and start at other cities since it is Monday.)
2nd week : fly from city 1 to city 2 on Monday, and play 3 days and work 4 days.
3rd week : stay at city 2, and play 3 days and work 4 days.
Example 2:
Input:flights = [[0,0,0],[0,0,0],[0,0,0]], days = [[1,1,1],[7,7,7],[7,7,7]]
Output: 3
Explanation:
Ans = 1 + 1 + 1 = 3.Since there is no flights enable you to move to another city, you have to stay at city 0 for the whole 3 weeks.
For each week, you only have one day to play and six days to work.
So the maximum number of vacation days is 3.
Example 3:
Input:flights = [[0,1,1],[1,0,1],[1,1,0]], days = [[7,0,0],[0,7,0],[0,0,7]]
Output: 21
Explanation:
Ans = 7 + 7 + 7 = 21One of the best strategies is:
1st week : stay at city 0, and play 7 days.
2nd week : fly from city 0 to city 1 on Monday, and play 7 days.
3rd week : fly from city 1 to city 2 on Monday, and play 7 days.
Note:
- N and K are positive integers, which are in the range of [1, 100].
- In the matrix flights, all the values are integers in the range of [0, 1].
- In the matrix days, all the values are integers in the range [0, 7].
- You could stay at a city beyond the number of vacation days, but you should work on the extra days, which won’t be counted as vacation days.
- If you fly from the city A to the city B and take the vacation on that day, the deduction towards vacation days will count towards the vacation days of city B in that week.
- We don’t consider the impact of flight hours towards the calculation of vacation days.
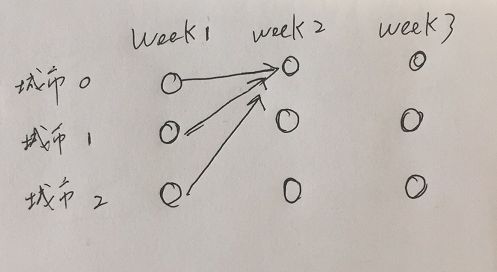
一道动态规划题,很可惜最近做了很多dp,但此dp还是没在有限时间内解决。它的阶段很明显,每周是一个阶段,更新则与城市与城市的航班有关。简单说一下思路,初始状态那家伙一定是在第一周的第0个城市,那他还有可能到第一周的第1...N-1个城市,只要有航班飞往那些城市即可,所以该dp记录dp[i][j],所代表的含义为在第j周时,第i个城市的最长休假天数。代码如下:
public int maxVacationDays(int[][] flights, int[][] days) {
int n = days.length;
int m = days[0].length;
int[][] dp = new int[n + 1][m + 1];
dp[1][1] = days[0][0];
for (int i = 1; i < m; i++) {
dp[1][i + 1] = dp[1][i] + days[0][i];
}
for (int j = 1; j < n; j++) {
if (flights[0][j] == 1) {
dp[j + 1][1] = days[j][0];
}
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
if (flights[k][j] == 1 || k == j) {
dp[j + 1][i + 1] = Math.max(dp[j + 1][i + 1],
dp[k + 1][i] + (dp[k + 1][i] == 0 ? 0 : days[j][i]));
}
}
}
}
int max = 0;
for (int i = 0; i < n + 1; i++) {
max = Math.max(dp[i][m], max);
}
return max;
}dp[j + 1][i + 1] = Math.max(dp[j + 1][i + 1],dp[k+1][i] + days[j][i])注意上述代码的一些细节问题,首先dp初始化全为0,这是否合理?为何分成了三部分循环,有没有办法把它们合并在一块?在更新规则中,多了遇0判断,产生它的原因是什么?
先来看看优秀的代码如何优美的解决上述问题,代码如下:
public int maxVacationDays(int[][] flights, int[][] days) {
int n = flights.length;
int k = days[0].length;
int[][] dp = new int[k + 1][n];
for (int[] ints : dp) {
Arrays.fill(ints, Integer.MIN_VALUE / 2);
}
dp[0][0] = 0;
for (int week = 1; week <= k; week++) {
for (int city = 0; city < n; city++) {
for (int lastCity = 0; lastCity < n; lastCity++) {
if (city == lastCity || flights[lastCity][city] == 1) {
dp[week][city] = Math.max(dp[week][city],
dp[week - 1][lastCity] + days[city][week - 1]);
}
}
}
}
int answer = 0;
for (int i : dp[k]) {
answer = Math.max(answer, i);
}
return answer;
}对比上述代码,下者思路要清楚很多,首先
int[][] dp = new int[k+1][n] // k + 1 表示week, n表示city为啥k+1是k+1而不是k,n是n而不是n+1。明确阶段和状态的区别,阶段是有生成的先后顺序,而状态理论上无序。该题很明显week是阶段,下周都由上周生成,而城市只是中间状态(结点)。
另外一个原因在于k+1,则预留了一个初始态,那么更新就可以从初始态0开始,而非第一周开始,这也是为什么我的代码当中出现了多个循环的原因,我虽然同样用了dp[k+1][n+1],但是依旧用第一周当初始态(代码呈现),所以出现很多奇怪的边界条件的判断。
for (int[] ints : dp) {
Arrays.fill(ints, Integer.MIN_VALUE / 2);
}
dp[0][0] = 0;这部分的代码也很巧妙,初始态第0周为[0,INF,INF],这说明雇员的刚开始在city 0,而不在其他城市。这就意味着当有city == lastCity条件时,减少了一次判断,即时加上当天的假期数,该值还是很小的值。而这避免了0值的尴尬,这也就是为什么我的代码当中出现了0的判断。
其实为什么有lastCity == city是为了针对一种特殊的情况,即这家伙一直呆在某个城市,只要有航班能飞到某个城市,而后续该城市成了孤岛,这意味着他必须在此度过余生了。而初始状态,它呆在0城市,所以天然的有dp[0][0] = 0 not INF。
最后针对最后一个阶段的n个状态求个最大值即可。