Leetcode Weekly Contest 174
5328. The K Weakest Rows in a Matrix
1. 题意
给定一个二维矩阵mat,每一行由0,1组成, 1代表士兵,0代表平民,如果一行士兵更多,则称这一行的战斗力更强,求从弱到强的k行,返回下标。
2. 思路
简单的统计每一行中1的个数,然后进行排序即可
这里不仅要记录每一行中1的个数,还得记录每一行的下标!!!
这里不能使用元组来做,因为元组不支持赋值操作,也就是不能进行修改!
第一种方法:通过dict来存储, 浪费存储空间了!
这里得学会对dict进行排序,排序后返回了一个元组的数组
c = sorted(cc.items(), key = lambda d:d[1]) # 变成元组了啊!
第二种方法:通过二维数组来存储!
cc.sort(key = lambda c:c[1]) # 数组按照第二项进行从小往大排序
3. python实现
class Solution(object):
def kWeakestRows(self, mat, k):
"""
:type mat: List[List[int]]
:type k: int
:rtype: List[int]
"""
# ----------------刚刚比赛时写的并不好啊1------------------------------------
# cc = collections.defaultdict(int)
# for i in range(len(mat)):
# for j in range(len(mat[0])):
# if mat[i][j] == 1:
# cc[i] += 1
# else:
# if j==0:
# cc[i] = 0
# break
# c = sorted(cc.items(), key = lambda d:d[1]) # 变成元组了啊!
# # print(c)
# res = []
# for nums in c:
# if k > 0:
# res.append(nums[0])
# k -= 1
# return res
m, n = len(mat), len(mat[0])
# 直接用元组来存,(i,j)表示第i行中有j个1
cc = [[0,0] for i in range(m)]
for i in range(m):
cc[i][0] = i
for j in range(n):
if mat[i][j] == 1:
cc[i][1] += 1
else: # 一行中1是连续的啊
break
cc.sort(key = lambda c:c[1]) # 数组按照第二项进行从小往大排序
res = []
for i in range(k):
res.append(cc[i][0])
return res
5329. Reduce Array Size to The Half
1. 题意
给定一个一维数组arr,你可以选择一个整数集合,然后把数组中所有出现在集合中的数都去掉,最后让数组的长度减半!求最短的集合
比如arr = [3,3,3,3,5,5,5,2,2,7], set = {3,5} or {3,2} or {5,2} , 删除set中在arr中出现的数,都可以导致arr的长度减半!因此最短的集合的长度为2!
2.思路
统计arr中每一个数出现的次数,然后从大到小排序,当然是从出现最多的数开始删除!
3. Python实现
class Solution(object):
def minSetSize(self, arr):
"""
:type arr: List[int]
:rtype: int
"""
n = len(arr)
cc = collections.Counter(arr)
c = sorted(cc.items(), key = lambda d:-d[1]) # 按照出现次数排序
res = 0
count = 0
# print(c)
for tup in c:
if count < n//2:
count += tup[1]
res += 1
else:
break
return res
5330. Maximum Product of Splitted Binary Tree
1. 题意
给定一棵二叉树root, 然后每次删除其中一条边,把二叉树分裂成两棵二叉树,求两棵二叉树的和的乘积的最大值!
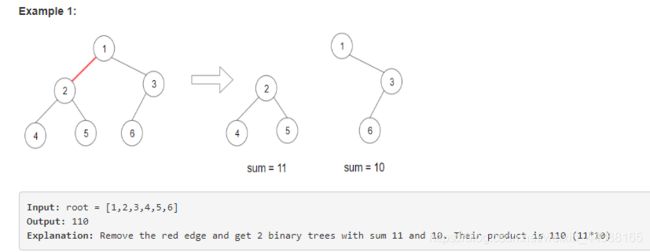
2. 思路
我看到这道题,立马就思考去掉边怎么操作?还有就是子树如何求和?
数据量最大有50000,并且数值在0-10000之间,可以看出节点有重复值,并且时间复杂度不能是O(N^2),否则就会超时!
所以最好就是在遍历的时候顺便求子树的和,并且顺便也求两个子树之间的乘积,这样时间复杂度就控制在O(N)了。
做这道题之前最好做一下另外一道题:
程序员面试算法宝典—解题总结: 第三章 二叉树 3.4 如何求一棵二叉树的最大子树和
会求二叉树的子树和就会做这道题了!
3. python实现
class Solution(object):
def maxProduct(self, root):
"""
:type root: TreeNode
:rtype: int
"""
self.allsum = 0
self.product = float('-inf')
def dfs(root): # 求树的所有节点之和
if not root: return
self.allsum += root.val
dfs(root.left)
dfs(root.right)
def post(root): # 返回以root为根的子树的和,后序遍历,自底向上来遍历
if not root: return 0
lsums = post(root.left)
rsums = post(root.right)
subsum = lsums + rsums + root.val
# print(subsum, (self.allsum-subsum), subsum* (self.allsum-subsum))
self.product = max(self.product, subsum* (self.allsum-subsum))
return subsum
dfs(root)
post(root)
return self.product % 1000000007