Python描述数据结构之图的遍历篇

前言

  本篇章主要介绍图的遍历算法，包括深度优先遍历和广度优先遍历，并用Python代码实现。

1. 创建图

  图的遍历过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所用的存储结构。以下图为例：

  为了方便测试，先建立一个图，这里用邻接表表示图：

class Graph(object):
    """
    使用邻接表存储图
    """
    def __init__(self, kind):
        # 图的类型: 无向图, 有向图, 无向网, 有向网
        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,
        self.kind = kind
        # 邻接表
        self.vertices = []
        # 当前顶点数
        self.vexnum = 0
        # 当前边(弧)数
        self.arcnum = 0

    def CreateGraph(self, vertex_list, edge_list):
        """
        创建图
        :param vertex_list: 顶点列表
        :param edge_list: 边列表
        :return:
        """
        self.vexnum = len(vertex_list)
        self.arcnum = len(edge_list)
        for vertex in vertex_list:
            vertex = Vertex(vertex)
            self.vertices.append(vertex)
        for edge in edge_list:
            tailindex = self.LocateVertex(edge[0])
            headindex = self.LocateVertex(edge[1])
            self.InsertArc(tailindex, headindex)

    def LocateVertex(self, vertex):
        """
        定位顶点在邻接表中的位置
        :param vertex:
        :return:
        """
        index = 0
        while index < self.vexnum:
            if self.vertices[index].data == vertex:
                return index
            else:
                index += 1

    def InsertArc(self, tailindex, headindex):
        """
        建立邻接表
        :param tailindex:
        :param headindex:
        :return:
        """
        if self.kind == 'Undigraph':
            # 无向图
            TailArc = Arc(tailindex)
            HeadArc = Arc(headindex)

            # 对于边A-B, tail为A, head为B
            # 定义顶点A对应的单链表
            # 边结点(单链表)
            # 头插法
            HeadArc.NextArc = self.vertices[tailindex].FirstArc
            # 顶点结点
            self.vertices[tailindex].FirstArc = HeadArc
            # 定义顶点B对应的单链表
            TailArc.NextArc = self.vertices[headindex].FirstArc
            self.vertices[headindex].FirstArc = TailArc
        elif self.kind == 'Digraph':
            # 有向图
            # 对于弧A->B
            HeadArc = Arc(headindex)
            HeadArc.NextArc = self.vertices[tailindex].FirstArc
            self.vertices[tailindex].FirstArc = HeadArc

    def VisitVertex(self, index):
        """
        打印这一顶点
        :param index:
        :return:
        """
        print(self.vertices[index].data, end=' ')

    def GetFirstAdjacentVertex(self, index):
        """
        获取顶点的第一个邻接点的下标
        :param index:
        :return:
        """
        # 与该顶点相关联的第一条边
        FirstArc = self.vertices[index].FirstArc
        if FirstArc is not None:
            # 与该边邻接的另一个顶点的索引
            return FirstArc.adjacent

    def GetNextAdjacentVertex(self, v, w):
        """
        v是顶点结点, w是单链表的结点, 即边结点
        这个函数就是根据顶点v, 先找到顶点w, 然后再找到w指向的C的下一个邻接点
        :param v:
        :param w:
        :return:
        """
        ArcLink = self.vertices[v].FirstArc
        while ArcLink is not None:
            if ArcLink.adjacent == w:
                if ArcLink.NextArc is not None:
                    # w指向的C的下一个结点
                    return ArcLink.NextArc.adjacent
                else:
                    # w没有指向C的下一个结点了, 即w就是最后一个
                    return None
            else:
                # 不相等, 说明该结点不是w, 继续找w结点
                ArcLink = ArcLink.NextArc

  有关邻接表中顶点结点Vertex()和边结点Arc()的定义可以参考这篇博客，这里就不在贴出相应的代码了。

  根据上述代码，建立的邻接表为：

2. 深度优先遍历

  深度优先遍历$(Depth$ $First$ $Search,DFS)$类似于二叉树的先序遍历，它的特点是尽可能深地去遍历整个图。
  基本思想就是先访问图中某一个起始顶点$v$，然后由$v$出发，访问与$v$邻接且未被访问的任意顶点$w_1$，再访问与$w_1$邻接且未被访问的任意顶点$w_2$，一直这样向下深入访问。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问，则从该顶点开始继续上述的搜索过程，直至图中所有顶点都被访问过。

  所以该图的遍历过程为：从顶点$A$开始，按照建立的邻接表，它的第一个邻接点是$D$，所以第一步就是从顶点$A$到顶点$D$，即图中的1号红色线；然后访问顶点$D$的邻接点$B$，即图中2号橙色线；然后访问顶点$B$的邻接点$E$，即图中3号绿色线；然后访问顶点$E$的邻接点$C$，即图中4号蓝色线；其实这时就已经访问完了，程序访问到顶点$C$时，继续找它的邻接点，这时候找到的是$E$，它已经被访问过，然后就找顶点$C$对应的单链表中$E$指向的$C$的下一个邻接点，这时候找到的是$A$，发现它也被访问过，然后就继续找顶点$C$对应的单链表中$A$指向的$C$的下一个邻接点，根据单链表可知，$A$指向空。这时，这条路径上所有的顶点已经正式访问结束，然后回退到最近被访问过的顶点$E$，重复上述过程，然后再回退到$B$，直至结束。遍历的结果就是$ADBEC$。
  DFS算法是一个递归算法，需要借助一个递归工作栈，所以空间复杂度为$O(n)$。以邻接矩阵表示图时，查找每个顶点的邻接点所有需要的时间为$O(n)$，所以查找图中所有顶点的邻接点所需要的时间为$O(n^2)$；以邻接表表示图时，访问顶点所需要的时间为$O(n)$，查找所有顶点的邻接点所需要的时间为$O(e)$，所以总的时间复杂度为$O(n+e)$。
  以邻接表表示图的深度优先遍历：

    def DFSTraverse(self):
        # 使用visited列表来标记图中的顶点是否已被访问
        visited = [False] * self.vexnum
        index = 0
        while index < self.vexnum:
            # 遍历每一个顶点
            if not visited[index]:
                # 该顶点为False, 还未被访问
                self.DFS(visited, index)
            index += 1

    def DFS(self, visited, v):
        visited[v] = True
        # 先访问顶点v
        self.VisitVertex(v)
        # w是v的一个邻接点
        w = self.GetFirstAdjacentVertex(v)
        while w is not None:
            # v的所有邻接点
            if not visited[w]:
                # 该顶点还未被访问, 向下遍历
                self.DFS(visited, w)
            # 下一个邻接点
            w = self.GetNextAdjacentVertex(v, w)

3. 广度优先遍历

  广度优先遍历$(Breadth$ $First$ $Search,BFS)$类似于二叉树的层次遍历，它的特点是尽可能广地去遍历整个图。
  基本思想就是先访问图中某一个起始顶点$v$，然后由$v$出发，依次访问$v$的各个未访问过的邻接顶点$w_1,w_2,\dots ,w_n$，然后再从$w_1,w_2,\dots ,w_n$依次出发，访问它们的所有未被访问的邻接点，一直这样类似于于一层一层地访问，直至所有顶点都被访问过。如果图中还有顶点未被访问，则另选一个图中未被访问过的结点作为起始结点重复上述过程。

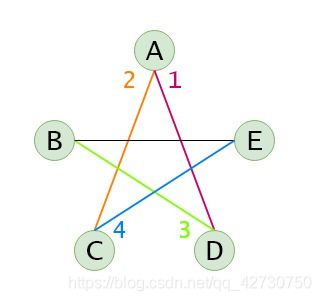
  所以该图的遍历过程为：从顶点$A$开始，按照建立的邻接表，它的第一个邻接点是$D$，所以第一步就是从顶点$A$到顶点$D$，即图中的1号红色线；然后继续访问顶点$A$的邻接点$C$，即图中2号橙色线；这个时候$DC$已经入队了，然后访问顶点$D$的邻接点$B$，即图中3号绿色线，然后继续访问顶点$D$的邻接点$A$，发现已被访问过；然后访问顶点$C$的邻接点$E$，即图中4号蓝色线，然后继续访问顶点$C$的邻接点$A$，发现已被访问过；这个时候$BE$已经入队了，然后继续访问，直至队列为空，结束。遍历的结果就是$ADCBE$。
  广度优先遍历的过程是以$v$为起始点，由近至远依次访问和$v$有路径相同且路径长度为$1,2,\dots$的顶点，是一种分层的查找过程，每向下一层，都可能访问一批的顶点，所以它没有回退的情况，即不是一个递归的过程。
  在实现广度优先遍历时需要一个辅助队列，来记录当前访问顶点的下一层顶点：

    def BFSTraverse(self):
        # 使用visited列表来标记图中的顶点是否已被访问
        visited = [False] * self.vexnum
        # 使用一个辅助队列, 默认队列长度为10
        queue = CircularSequenceQueue()
        index = 0
        # 从索引为0的顶点开始遍历
        while index < self.vexnum:
            # 遍历每一个顶点
            if not visited[index]:
                self.BFS(visited, index, queue)
            index += 1

    def BFS(self, visited, v, queue):
        visited[v] = True
        self.VisitVertex(v)
        # 起始顶点v入队
        queue.EnQueue(v)
        while not queue.IsEmpty():
            # 辅助队列不为空, 说明该顶点的邻接点还没有访问
            # 该顶点出队, 找它的邻接点
            vertex = queue.DeQueue()
            # w是v的一个临界点
            w = self.GetFirstAdjacentVertex(vertex)
            while w is not None:
                # v的所有邻接点
                if not visited[w]:
                    # 该顶点未被访问
                    visited[w] = True
                    self.VisitVertex(w)
                    queue.EnQueue(w)
                # 下一个邻接点
                w = self.GetNextAdjacentVertex(vertex, w)

  这里使用了前面介绍过的循环队列来作为辅助队列，代码已在这篇博客里面给出，这里不再叙述。

4. 代码测试

  测试代码如下：

if __name__ == '__main__':
    graph = Graph(kind='Undigraph')
    graph.CreateGraph(vertex_list=['A', 'B', 'C', 'D', 'E'],
                      edge_list=[('A', 'C'), ('A', 'D'), ('B', 'D'), ('B', 'E'), ('C', 'E')])
    print('深度优先遍历: ', end='')
    graph.DFSTraverse()
    print('\n广度优先遍历: ', end='')
    graph.BFSTraverse()

  运行结果如下：