FastICA独立成分 - python实现 - C++实现
FastICA 步骤:
1. 对观测数据 X 进行中心化处理,使样本的每个属性均值为0
2. 求出样本矩阵的协方差矩阵 Cx
3. 用主成分分析得到白化矩阵 W0=Λ-1/2UT 对 其中Λ、U分别是Cx的特征值、特征向量
4. 计算正交阵Z=W0*X, Z维数可以根据主成分的占比,小于样本属性数
5. 初始化权重矩阵(随机的)Wp 、设迭代次数count、停机误差Critical
6. 令Wp=E{ Z*g(WTZ) } - E{ g'(WTZ) }*W 其中非线性函数g(x),可取g1(x)=tanh(x)或g2(y)=y*exp(-y2/2)或g3(y)=y3等非线性函数
7. SZ=Wp*Z 为分离后的信号矩阵
import matplotlib.pyplot as plt
import numpy as np
from numpy import linalg as LA
C=200 #样本数
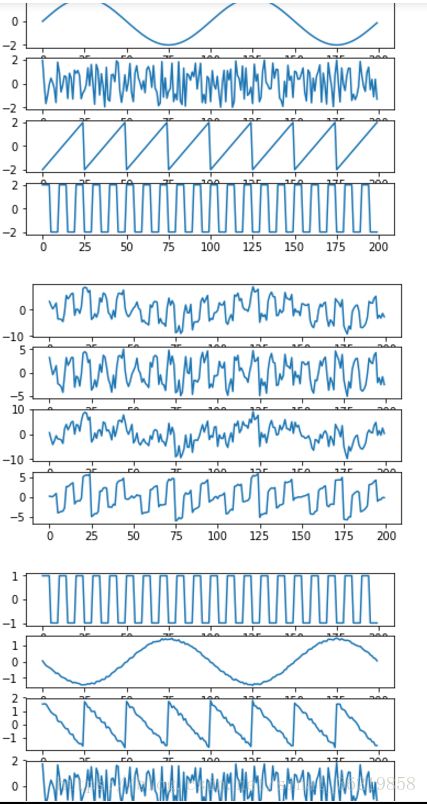
x=np.arange(C)
s1=2*np.sin(0.02*np.pi *x)#正弦信号
a=np.linspace(-2,2,25)
s2= np.array([a,a,a,a,a,a,a,a]).reshape(200,)#锯齿信号
s3=np.array(20*(5*[2]+5*[-2])) #方波信号
s4 =4*(np.random.random([1,C])-0.5).reshape(200,) #随机信号
# drow origin signal
ax1 = plt.subplot(411)
ax2 = plt.subplot(412)
ax3 = plt.subplot(413)
ax4 = plt.subplot(414)
ax1.plot(x,s1)
ax2.plot(x,s2)
ax3.plot(x,s3)
ax4.plot(x,s4)
plt.show()
s=np.array([s1,s2,s3,s4]) #合成信号
ran=2*np.random.random([4,4]) #随机矩阵
mix=ran.dot(s) #混合信号
# drow mix signal
ax1 = plt.subplot(411)
ax2 = plt.subplot(412)
ax3 = plt.subplot(413)
ax4 = plt.subplot(414)
ax1.plot(x,mix.T[:,0])
ax2.plot(x,mix.T[:,1])
ax3.plot(x,mix.T[:,2])
ax4.plot(x,mix.T[:,3])
plt.show()
#mix=np.array([[1.1,2,3,4,1],
# [5,6,2,8,7],
# [6,2,5,1,3],
# [7,8,3,3,2]])
Maxcount=10000 # %最大迭代次数
Critical=0.00001 # %判断是否收敛
R,C=mix.shape
average=np.mean(mix, axis=1) #计算行均值,axis=0,计算每一列的均值
for i in range(R):
mix[i,:]=mix[i,:]- average[i] #数据标准化,均值为零
Cx=np.cov(mix)
value,eigvector = np.linalg.eig(Cx)#计算协方差阵的特征值
val=value**(-1/2)*np.eye(R, dtype=float)
White=np.dot(val ,eigvector.T) #白化矩阵
Z=np.dot(White,mix) #混合矩阵的主成分Z,Z为正交阵
#W = np.random.random((R,R))# 4x4
W=0.5*np.ones([4,4])#初始化权重矩阵
for n in range(R):
count=0
WP=W[:,n].reshape(R,1) #初始化
LastWP=np.zeros(R).reshape(R,1) # 列向量;LastWP=zeros(m,1);
while LA.norm(WP-LastWP,1)>Critical:
#print(count," loop :",LA.norm(WP-LastWP,1))
count=count+1
LastWP=np.copy(WP) # %上次迭代的值
gx=np.tanh(LastWP.T.dot(Z)) # 行向量
for i in range(R):
tm1=np.mean( Z[i,:]*gx )
tm2=np.mean(1-gx**2)*LastWP[i] #收敛快
#tm2=np.mean(gx)*LastWP[i] #收敛慢
WP[i]=tm1 - tm2
#print(" wp :", WP.T )
WPP=np.zeros(R) #一维0向量
for j in range(n):
WPP=WPP+ WP.T.dot(W[:,j])* W[:,j]
WP.shape=1,R
WP=WP-WPP
WP.shape=R,1
WP=WP/(LA.norm(WP))
if(count ==Maxcount):
print("reach Maxcount,exit loop",LA.norm(WP-LastWP,1))
break
print("loop count:",count )
W[:,n]=WP.reshape(R,)
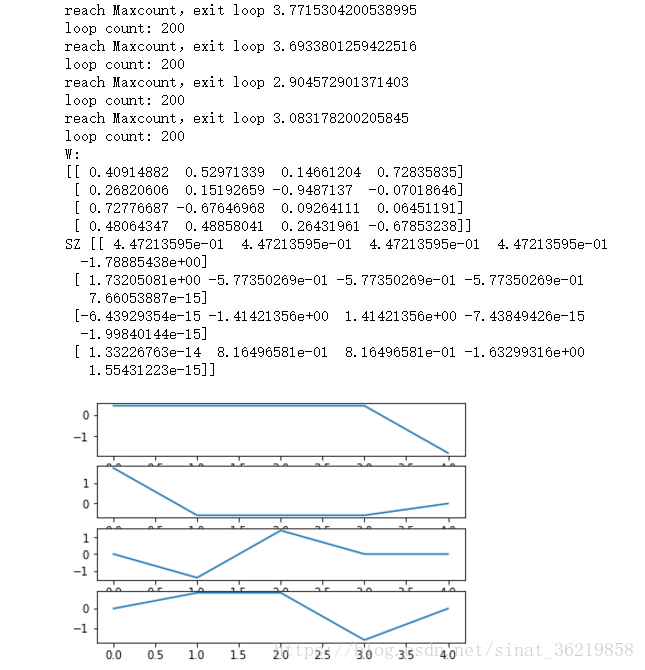
SZ=W.T.dot(Z)
# plot extract signal
x=np.arange(0,C)
ax1 = plt.subplot(411)
ax2 = plt.subplot(412)
ax3 = plt.subplot(413)
ax4 = plt.subplot(414)
ax1.plot(x, SZ.T[:,0])
ax2.plot(x, SZ.T[:,1])
ax3.plot(x, SZ.T[:,2])
ax4.plot(x, SZ.T[:,3])
plt.show()结果示意图:
下面为C++代码实现,和python有相同的结果。
#include "matrix.h"
/*
数据格式:行数是属性数,每一列是一个样本,一下为实例数据
1.1 2 3 4 1
5 6 2 8 7
6 2 5 1 3
7 8 3 3 2
*/
int main()
{
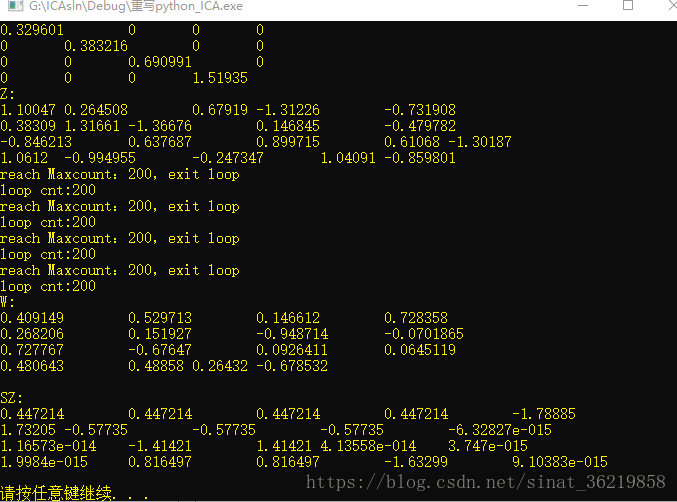
int R = 4;
int C = 5;
int maxcnt= 200;
Matrix src(R, C); // 原始数据
cin >> src;
src.zeromean(false);
Matrix Cov = src.T().cov(); //样本的协方差矩阵
Matrix eigval = Cov.eig_val();
cout << "eigval \n" << eigval << endl;
Matrix eigvect = Cov.eig_vect();
cout << "eigvect \n" << eigvect << endl;
eigval = eigval.exponent(-0.5);//每个特征值的 -0.5 次方
eigval.maxlimit(10000); ///超过10000,设置为0
cout << "eigval^-0.5 \n" << eigval;
Matrix white = eigval* eigvect.T(); //由特征值、特征向量组成白化矩阵
Matrix Z = white*src; //正交阵
cout << "Z:\n" << Z;
Matrix W(R, R, 0.5); //初始权值矩阵
for (size_t i = 0; i < R; i++)
{
int cnt = 0;
Matrix WP = W.getcol(i);
Matrix LastWP(R,1,0);
while ((WP - LastWP).norm1()>0.01)
{
cnt++;
LastWP = WP; //上次迭代的值
Matrix gx = (LastWP.T()*Z).mtanh();// 行向量
for (size_t j = 0; j < R; j++) //更新 WP
{
double tm1 = (Z.getrow(j).multi(gx) ).mean();
Matrix one(gx.Row(), gx.Col(), 1.0);
double tm2 = (one - gx.exponent(2)).mean()*LastWP[j][0];
WP[j][0] = tm1 - tm2;
}
Matrix WPP(R, 1, 0);
for (size_t k = 0; k < i; k++)
{
double tem = (WP.T()*W.getcol(k))[0][0];
WPP = WPP + tem * W.getcol(k);
}
WP = WP - WPP;
WP = WP / (WP.norm2());
if (cnt == maxcnt)
{
cout << "reach Maxcount:"<< maxcnt<<",exit loop" << endl;
break;
}
}
cout << "loop cnt:" << cnt << endl;
for (size_t s = 0; s < R; s++)
{
W[s][i] = WP[s][0];
}
}
cout << "W:\n" << W << endl;
Matrix SZ = W.T()*Z;
cout << "SZ:\n" << SZ<测试数据的结果为:
与python结果对比:
参考文献:
1,https://en.wikipedia.org/wiki/Independent_component_analysis
2,https://blog.csdn.net/zb1165048017/article/details/48464573
c++引用的矩阵类Matrix.h
#include
#include // std::ifstream
#include
#include
using namespace std;
class Matrix
{
private:
unsigned row, col, size;
double *pmm;//数组指针
public:
Matrix(unsigned r, unsigned c) :row(r), col(c)//非方阵构造
{
size = r*c;
if (size>0)
{
pmm = new double[size];
for (unsigned j = 0; j0)
{
pmm = new double[size];
for (unsigned j = 0; j0)
{
pmm = new double[size];
for (unsigned j = 0; j>(istream&, Matrix&);
friend ofstream &operator<<(ofstream &out, Matrix &obj); // 输出到文件
friend ostream &operator<<(ostream&, Matrix&); // 输出到屏幕
friend Matrix operator+(const Matrix&, const Matrix&);
friend Matrix operator-(const Matrix&, const Matrix&);
friend Matrix operator*(const Matrix&, const Matrix&); //矩阵乘法
friend Matrix operator*(double, const Matrix&); //矩阵乘法
friend Matrix operator*(const Matrix&, double); //矩阵乘法
friend Matrix operator/(const Matrix&, double); //矩阵 除以单数
Matrix multi(const Matrix&); // 对应元素相乘
Matrix mtanh(); // 对应元素相乘
unsigned Row()const{ return row; }
unsigned Col()const{ return col; }
Matrix getrow(size_t index); // 返回第index 行,索引从0 算起
Matrix getcol(size_t index); // 返回第index 列
Matrix cov(_In_opt_ bool flag = true); //协方差阵 或者样本方差
double det(); //行列式
Matrix solveAb(Matrix &obj); // b是行向量或者列向量
Matrix diag(); //返回对角线元素
//Matrix asigndiag(); //对角线元素
Matrix T()const; //转置
void sort(bool);//true为从小到大
Matrix adjoint();
Matrix inverse();
void QR(_Out_ Matrix&, _Out_ Matrix&)const;
Matrix eig_val(_In_opt_ unsigned _iters = 1000);
Matrix eig_vect(_In_opt_ unsigned _iters = 1000);
double norm1();//1范数
double norm2();//2范数
double mean();// 矩阵均值
double*operator[](int i){ return pmm + i*col; }//注意this加括号, (*this)[i][j]
void zeromean(_In_opt_ bool flag = true);//默认参数为true计算列
void normalize(_In_opt_ bool flag = true);//默认参数为true计算列
Matrix exponent(double x);//每个元素x次幂
Matrix eye();//对角阵
void maxlimit(double max,double set=0);//对角阵
};
//友元仅仅是指定了访问权限,不是一般意义的函数声明,最好在类外再进行一次函数声明。
//istream &operator>>(istream &is, Matrix &obj);
//ostream &operator<<(ostream &is, Matrix &obj);
//对称性运算符,如算术,相等,应该是普通非成员函数。
//Matrix operator*( const Matrix&,const Matrix& );
//Matrix operator+( const Matrix&,const Matrix& );
//dets递归调用
Matrix Matrix::mtanh() // 对应元素 tanh()
{
Matrix ret(row, col);
for (unsigned i = 0; i brow ? 0 : 1; //bb中小于arow的行,同行赋值,等于的错过,大于的加一
for (int j = 0; jmax ? 0 : pmm[i*col + j];
}
}
}
Matrix Matrix::eye()//对角阵
{
for (unsigned i = 0; i< row; i++)
{
for (unsigned j = 0; j < col; j++)
{
if (i == j)
{
pmm[i*col + j] = 1.0;
}
}
}
return *this;
}
void Matrix::zeromean(_In_opt_ bool flag)
{
if (flag == true) //计算列均值
{
double *mean = new double[col];
for (unsigned j = 0; j < col; j++)
{
mean[j] = 0.0;
for (unsigned i = 0; i < row; i++)
{
mean[j] += pmm[i*col + j];
}
mean[j] /= row;
}
for (unsigned j = 0; j < col; j++)
{
for (unsigned i = 0; i < row; i++)
{
pmm[i*col + j] -= mean[j];
}
}
delete[]mean;
}
else //计算行均值
{
double *mean = new double[row];
for (unsigned i = 0; i< row; i++)
{
mean[i] = 0.0;
for (unsigned j = 0; j < col; j++)
{
mean[i] += pmm[i*col + j];
}
mean[i] /= col;
}
for (unsigned i = 0; i < row; i++)
{
for (unsigned j = 0; j < col; j++)
{
pmm[i*col + j] -= mean[i];
}
}
delete[]mean;
}
}
void Matrix::normalize(_In_opt_ bool flag)
{
if (flag == true) //计算列均值
{
double *mean = new double[col];
for (unsigned j = 0; j < col; j++)
{
mean[j] = 0.0;
for (unsigned i = 0; i < row; i++)
{
mean[j] += pmm[i*col + j];
}
mean[j] /= row;
}
for (unsigned j = 0; j < col; j++)
{
for (unsigned i = 0; i < row; i++)
{
pmm[i*col + j] -= mean[j];
}
}
///计算标准差
for (unsigned j = 0; j < col; j++)
{
mean[j] = 0;
for (unsigned i = 0; i < row; i++)
{
mean[j] += pow(pmm[i*col + j],2);//列平方和
}
mean[j] = sqrt(mean[j] / row); // 开方
}
for (unsigned j = 0; j < col; j++)
{
for (unsigned i = 0; i < row; i++)
{
pmm[i*col + j] /= mean[j];//列平方和
}
}
delete[]mean;
}
else //计算行均值
{
double *mean = new double[row];
for (unsigned i = 0; i< row; i++)
{
mean[i] = 0.0;
for (unsigned j = 0; j < col; j++)
{
mean[i] += pmm[i*col + j];
}
mean[i] /= col;
}
for (unsigned i = 0; i < row; i++)
{
for (unsigned j = 0; j < col; j++)
{
pmm[i*col + j] -= mean[i];
}
}
///计算标准差
for (unsigned i = 0; i< row; i++)
{
mean[i] = 0.0;
for (unsigned j = 0; j < col; j++)
{
mean[i] += pow(pmm[i*col + j], 2);//列平方和
}
mean[i] = sqrt(mean[i] / col); // 开方
}
for (unsigned i = 0; i < row; i++)
{
for (unsigned j = 0; j < col; j++)
{
pmm[i*col + j] /= mean[i];
}
}
delete[]mean;
}
}
double Matrix::det()
{
if (col == row)
return dets(row, pmm);
else
{
cout << ("行列不相等无法计算") << endl;
return 0;
}
}
/
istream &operator>>(istream &is, Matrix &obj)
{
for (unsigned i = 0; i> obj.pmm[i];
}
return is;
}
ostream &operator<<(ostream &out, Matrix &obj)
{
for (unsigned i = 0; i < obj.row; i++) //打印逆矩阵
{
for (unsigned j = 0; j < obj.col; j++)
{
out << (obj[i][j]) << "\t";
}
out << endl;
}
return out;
}
ofstream &operator<<(ofstream &out, Matrix &obj)//打印逆矩阵到文件
{
for (unsigned i = 0; i < obj.row; i++)
{
for (unsigned j = 0; j < obj.col; j++)
{
out << (obj[i][j]) << "\t";
}
out << endl;
}
return out;
}
Matrix operator+(const Matrix& lm, const Matrix& rm)
{
if (lm.col != rm.col || lm.row != rm.row)
{
Matrix temp(0, 0);
temp.pmm = NULL;
cout << "operator+(): 矩阵shape 不合适,col:"
<< lm.col << "," << rm.col << ". row:" << lm.row << ", " << rm.row << endl;
return temp; //数据不合法时候,返回空矩阵
}
Matrix ret(lm.row, lm.col);
for (unsigned i = 0; ipmm[j])
{
tem = pmm[i];
pmm[i] = pmm[j];
pmm[j] = tem;
}
}
else
{
if (pmm[i]= 0; --m)
{
sum = 0;
for (unsigned j = m + 1; j < col; ++j)
{
sum += pmm[m * col + j] * ret.pmm[j * ret.col + count];
}
sum = -sum / pmm[m * col + m];
midSum += sum * sum;
ret.pmm[m * ret.col + count] = sum;
}
midSum = sqrt(midSum);
for (unsigned i = 0; i < ret.row; ++i)
{
ret.pmm[i * ret.col + count] /= midSum; //每次求出一个列向量
}
}
*this = matcopy;//恢复原始矩阵;
return ret;
}
Matrix Matrix::cov(bool flag)
{
//row 样本数,column 变量数
if (col == 0)
{
Matrix m(0);
return m;
}
double *mean = new double[col]; //均值向量
for (unsigned j = 0; jbi) //ai行的代数余子式是:小于ai的行,aa与bb阵,同行赋值
pi = 0;
else
pi = 1; //大于等于ai的行,取aa阵的ai+1行赋值给阵bb的bi行
if (aj>bj) //ai行的代数余子式是:小于ai的行,aa与bb阵,同行赋值
pj = 0;
else
pj = 1; //大于等于ai的行,取aa阵的ai+1行赋值给阵bb的bi行
bb[bi*(n - 1) + bj] = pmm[(bi + pi)*n + bj + pj];
}
}
if ((ai + aj) % 2 == 0) q = 1;//因为列数为0,所以行数是偶数时候,代数余子式为-1.
else q = (-1);
ret.pmm[ai*n + aj] = q*dets(n - 1, bb); //加符号变为代数余子式
}
}
delete[]bb;
return ret;
}
Matrix Matrix::inverse()
{
double det_aa = det();
if (det_aa == 0)
{
cout << "行列式为0 ,不能计算逆矩阵。" << endl;
Matrix rets(0);
return rets;
}
Matrix adj = adjoint();
Matrix ret(row);
for (unsigned i = 0; i