模拟退火算法求函数极值（含MATLAB代码实现）

二、模拟退火算法
1. 简介
     模拟退火算法的思想借鉴于固体的退火过程，当固体的温度很高时，内能比较大，固体内的粒子处于快速无序运动状态，当温度慢慢降低，固体的内能减小，粒子逐渐趋于有序，最终固体处于常温状态，内能达到最小，此时粒子最为稳定。

     白话理解：一开始为算法设定一个较高的值T（模拟温度），算法不稳定，选择当前较差解的概率很大；随着T的减小，算法趋于稳定，选择较差解的概率减小，最后，T降至终止迭代的条件，得到近似最优解。

2.算法思想及步骤

   （1）设置算法的参数：初始温度，结束温度，温度衰减系数，每个温度下的扰动次数，初始状态，初始解

   （2）对状态产生扰动，计算新状态下的解，比较两个解的大小，判断是否接受新的状态

   （3）在此温度下，对步骤（2）按设置的扰动次数重复进行扰动

   （4）对温度进行衰减，并在新的温度下重复（2）（3），直到结束温度

   （5）输出记录最优状态和最优解，算法结束

                                                

      

其中，P为算法选择较差解的概率；T 为温度的模拟参数；。

当T很大时，，此时算法以较大概率选择非当前最优解；
P的值随着T的减小而减小；
当时，，此时算法几乎只选择最优解，等同于贪心算法。
 

%VELASCO, Gimel David F.
%2012-58922
%Cmsc 191
%Simulated Annealing
%Final Exam
%for runs=1:3
clear;
tic;

%%%%%%%%%%%%%%%%%%%%%%%%%%%INPUT ARGUMENTS%%%%%%%Sir Joel, dito po%%%%%%%%%
CostF = 2; % | 1 - DE JONGS | 2 - AXIS PARALLEL HYPER-ELLIPSOID | 3 - ROTATED HYPER-ELLIPSOID | 4 - RASTRIGINS | ow - ACKLEYS |
nVar = 3; %染色体的等位基因数目，染色体长度
VarSize = zeros(nVar);
VarMin = -5.12; %upper bound of variable value
VarMax = 5.12; %lower bound of variable value
MaxIt = 100000;%最大迭代次数
T0 = 100;%初始温度
Tf = 0.000000000000001;%最终温度
alpha = 0.7;%温度下降率
%nPop = 10000;
nMove = 10000;
mu = 0.1;
%sigma = 0.25;
%%
%初始化
test_func = CostF;  %sets the number of w/c test function to be solved
ub = VarMax;
lb = VarMin;
ulb = ub;        %upper and lower bound
tpl = nVar;      %dimensions
x_sol = 2*ulb*(rand(1,tpl)-0.5);               %initial guess of the solution x
cooling_ratio = alpha;                    %sets the cooling ratio to 0.8  i.e. 0.7 < 0.8 < 0.9
num_neigh = nMove;                      %initializes the size of the random neighbors
cooling_sched = zeros(1);               %pre-allocation for speed
cooling_sched(1) = T0;                 %initializes the cooling schedule T0
iteration_array = zeros(1);
fittest_array = zeros(1);
solution_array = VarSize;

%%%%%%%%%%%%%%%%%%%%%%%%%SIMULATED ANNEALING%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
sched = 1;                                  %index
while cooling_sched(sched) > Tf     %终止条件
    T = cooling_sched(sched);               %sets the value of the temperature T
    for j=1:num_neigh
        r  = (cooling_ratio)^sched;             %is used so that the randomness of selecting a neighbor becomes narrower
        x_tmp = 2*ulb*r*(rand(1,tpl)-0.5);    %随机选择一个邻居进行比较
        if OBJFUNC(x_tmp,tpl,test_func) < OBJFUNC(x_sol,tpl,test_func)  %比较找最优的值
            x_sol = x_tmp;
        elseif OBJFUNC(x_tmp,tpl,test_func) > OBJFUNC(x_sol,tpl,test_func)  %if not, change the solution if it is lucky
            delta = OBJFUNC(x_tmp,tpl,test_func) - OBJFUNC(x_sol,tpl,test_func);
            p = P(delta,T);
            q = rand(1);
            if q <= p
                x_sol = x_tmp; 
            end
        end
    end

	fittest_array(sched) = OBJFUNC(x_sol,tpl,test_func);
	iteration_array(sched) = sched;
	solution_array(sched,:) = x_sol;

    cooling_sched(sched+1) = T*(cooling_ratio)^sched;
    sched = sched+1;
    if sched > MaxIt
    	break;
    end
end
%SOLUTION
if test_func == 1
fprintf('====================DE JONGS FUNCTION=============================\n');
elseif test_func == 2
fprintf('==============AXIS PARALLEL HYPER-ELLIPSOID FUNCTION==============\n');
elseif test_func == 3
fprintf('===============ROTATED HYPER-ELLIPSOID FUNCTION====================\n');
elseif test_func == 4
fprintf('====================RASTRIGINS FUNCTION===========================\n');
else
fprintf('=====================ACKLEYS FUNCTION=============================\n');
end
fprintf('==================SIMULATED ANNEALING=============================\n');
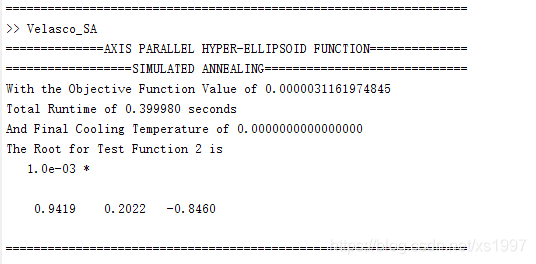
fprintf('With the Objective Function Value of %.16f\nTotal Runtime of %f seconds\nAnd Final Cooling Temperature of %.16f\n',OBJFUNC(x_sol,tpl,test_func),toc,cooling_sched(sched));
fprintf('The Root for Test Function %d is\n',test_func);
disp(x_sol)
fprintf('==================================================================\n');

figure
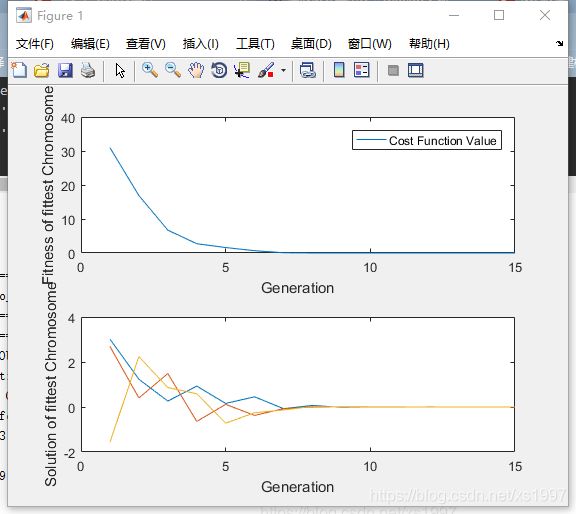
subplot(2,1,1);
plot(iteration_array,fittest_array);
legend('Cost Function Value');
xlabel('Generation');
ylabel('Fitness of fittest Chromosome');

solution_array = transpose(solution_array);
subplot(2,1,2);
plot(iteration_array,solution_array);
xlabel('Generation');
ylabel('Solution of fittest Chromosome');
%end

结果：