信号转换 | 如何将正弦波转换成方波？

模拟电子中对于信号进行波形转换是一个主要的处理问题。其中将输入的波形转换成方波信号是最为基础的转换方式。

对输入信号通过一个基本的比较器，便可以将输入的连续幅度的信号转换成幅值为离散取值（二值化）的信号，这个过程也称为对输入信号的二值化。

在有噪声的情况下，则需要通过带有一定回滞特性（Smith特性）来消除转换成安称重的信号抖动。

---

01问题的提出

本文中的内容是针对 信号转换的解题思路 中第一步“对信号整形”的处理。实验给出典型二值化的处理电路，并记录了一些基本的实验结果。

---

02实验方案验证

1.信号源的设置

在博文 利用STC8G1K08实现的数字信号合成模块 给出了可以通过无线蓝牙设置输出频率和波形的信号源模块。

由于该模块直接输出的信号的峰峰值只有0.7V左右，需要将其进行放大才能够满足后面信号实验的要求。

^{▲ 通过蓝牙设置信号模块及其放大电路}

下面是数字信号合成模块 AD9833 直接输出的正弦波信号。

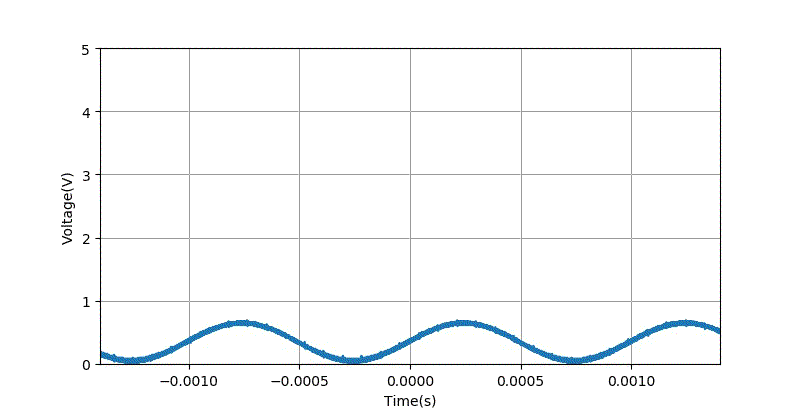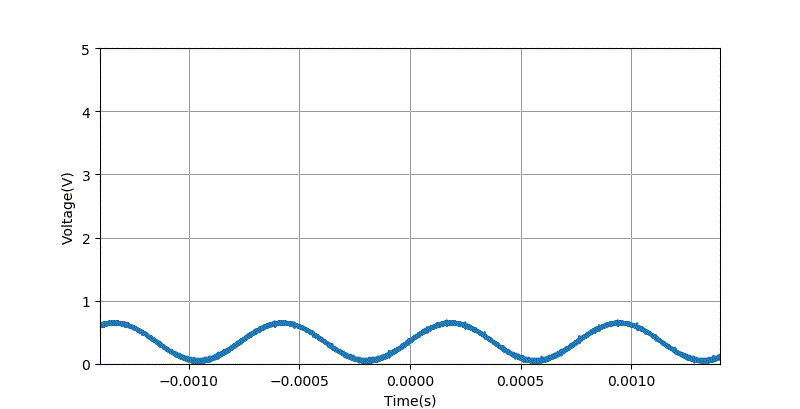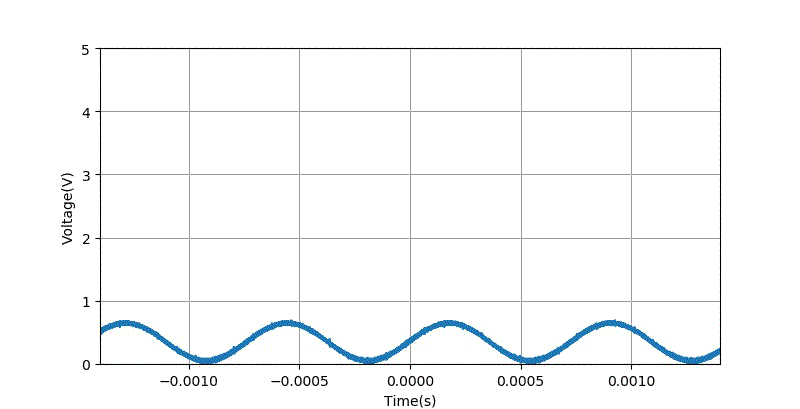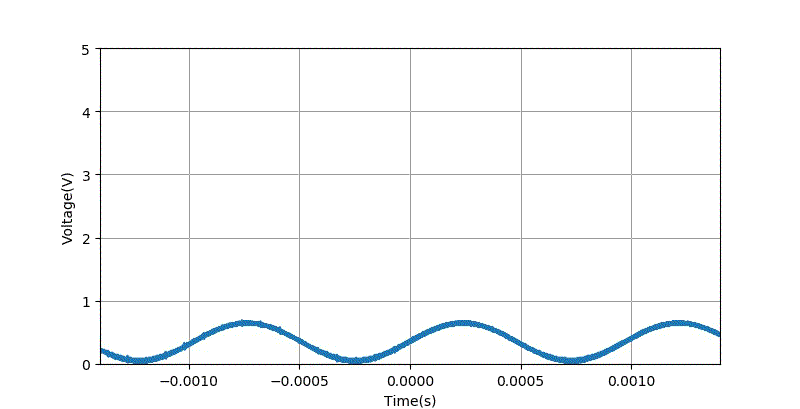
^{▲ 直接产生的信号波形}

经过LMV358进行放大之后，正弦波的波形基本上达到了0~5V之间。

^{▲ 经过LMV358放大之后的采集信号}

^{▲ 采集到的三角波信号}

AD9833可以直接产生0~5V的方波信号，只是此时的频率是设定频率值的一半。

^{▲ AD9833可以直接产生0~5V的方波信号}

采集和生成前面波形的Python程序如下：

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST1.PY                     -- by Dr. ZhuoQing 2020-05-22
#
# Note:
#============================================================
from headm import *
from tsmodule.tsvisa        import *
from tsmodule.tshardware    import *
from tsmodule.tsdraw        import *
#------------------------------------------------------------
ds6104open()
#zbcmd(b'ad9833triangle')
#zbcmd(b'ad9833sinusoidal')
zbcmd(b'ad9833square')
#------------------------------------------------------------
step = 20
flist = list(linspace(1000, 1500, step))
frvdim = flist + flist[-1::-1]
printf(frvdim)
#------------------------------------------------------------
pltgif = PlotGIF()
#------------------------------------------------------------
for f in frvdim:
    zbcmd(b'ad9833setfrequency %f'%f)
    time.sleep(.2)
    x, y = ds6104readcal(1)
    plt.clf()
    plt.plot(x, y)
    plt.xlabel('Time(s)')
    plt.ylabel('Voltage(V)')
    plt.axis([x[0], x[-1], 0, 5])
    plt.grid(True)
    plt.draw()
    plt.pause(.1)
    pltgif.append(plt)
printf("\a")
pltgif.save(r'd:\temp\1.gif')
#------------------------------------------------------------
#        END OF FILE : TEST1.PY
#============================================================

2.使用反相器来获得方波

由于输入信号的幅值很大，接近于0~5V之间，所以可以使用带有Smith输入特性的14触发器完成信号的整型。

^{▲ Smith反相器(74HCT14)}

下面给出了使用74HC14反相器得到的对输入正弦波、三角波的整形结果。可以从输出方波信号的上升沿和下降沿对应的输入信号的幅值差别，可以明显看到反相器的绘制特性。

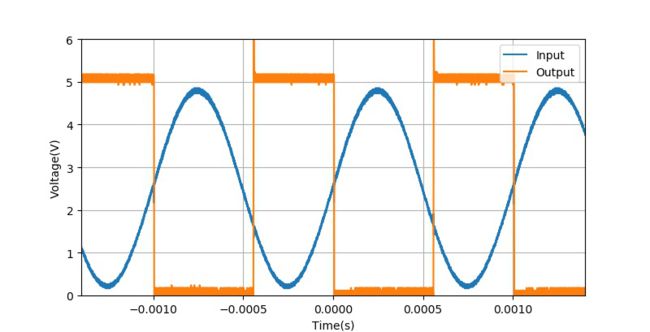
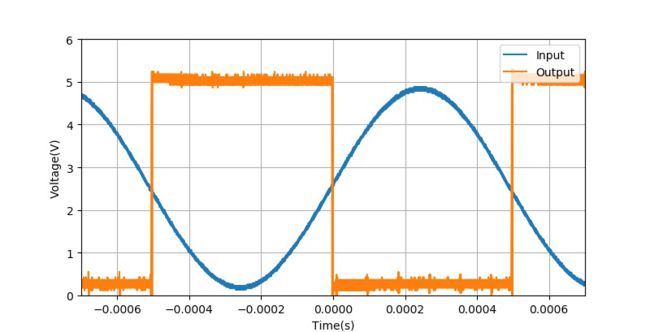
^{▲ 使用74HC14获得的方波}

^{▲ 使用74HC14获得的方波}

使用一个简单的具有Smith输入特性的反相器门电路可以比较方便的进行波形转换，但具有以下 缺点：

1. 输出波形不再对称。由于输入比较器的反转电压不再输入信号的过零中点上下对穿，这也使得输出方波不在是对称（50%占空比）。这在一些场合不太适合；
2. 对于输入信号的幅值敏感。随着输入信号的不同幅值，输出方波的占空比也会随之改变。特别当输入信号的幅值达不到回滞上下限的时候，输出就会是一个恒定值。

3.使用比较器来获得方波

LM311是常用到的高速信号比较器。它可以组成很多常用到的信号处理电路。

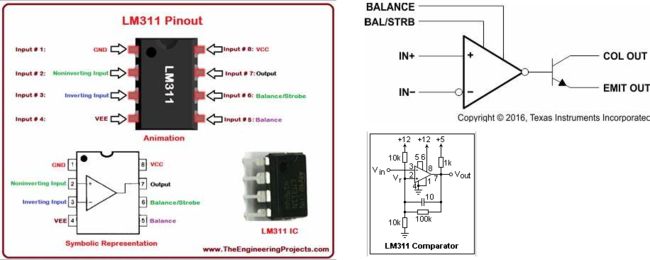
^{▲ LM311比较器}

使用该比较器可以对输入的信号进行转换成二值信号。

通过分压电路使得比较器的IN-，IN+处在电源电压的终点，输入信号通过电容耦合到IN+。这样就可以准确在带输入信号的过零点完成信号的整形了。

^{▲ 使用LM311比较器获得的波形}

如果信号带有噪声，就会在输出信号的跳变的时候出现一定量的抖动。如下图所示。这可以通过对输出信号进行低通滤波来消除这方面的影响。但最好的方法就是在比较器中引入正反馈形成Smith特性。

^{▲ 在过渡带引起的振荡}

下面就是从比较器的输出，通过20k电阻引至比较器的IN+，和IN+连接到中位电压的1k电阻分压形成正反馈。这样在整形的输入输出之间就形成了一定的回差。

通过这个回差（Smith）特性，可以消除输出信号在跳边沿出的抖动（Glitch）现象。

^{▲ 输入信号，输出信号，Smith反馈信号}

下面这张图是在增加了Smith特性之后，对输出跳边沿进行观察，已经没有了相应的抖动跳变了。

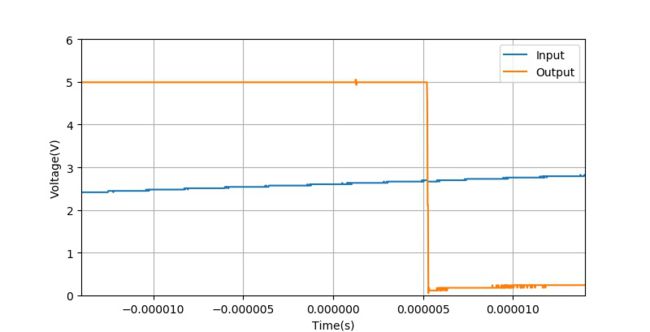
^{▲ 引入Smith特性之后，没有振荡波形了}

---

03方波的对称性

采集100次波形，计算波形的占空比。所得到的均值和方差分别为：

• 均值： 0.5038
• 方差：2.1642e-6

采集并进行测试的程序：

#------------------------------------------------------------
def dutyratio(d):
    dlist = [int(s == True) for s in list(array(d) > 2.5)]
    ddif = [int(s1 != s2) for s1,s2 in zip(dlist[0:-1], dlist[1:])]
    changeid = nonzero(ddif)[0]
    printf(changeid)
    return (changeid[1] - changeid[0])/(changeid[2] - changeid[0])

ratiodim = []

for i in range(100):
    x1,y1,y2 = ds6104readcal(1, 2)
    r = dutyratio(y2)
    ratiodim.append(r)
    printff(i, r)

tspsave('ratio', r = ratiodim)
printff(mean(ratiodim), var(ratiodim))
#------------------------------------------------------------

r=[0.50,0.51,0.51,0.51,0.51,0.50,0.50,0.51,0.50,0.51,0.50,0.50,0.50,0.50,0.50,0.50,0.51,0.50,0.51,0.51,0.51,0.50,0.50,0.50,0.51,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50,0.50]

---

04结论

通过LM311可以对输入的幅值连续的模拟信号进行二值化（整形）。通过加入少量的回滞（Smith）特性，可以消除输入信号中高频噪声在输出信号中所带来的抖动。

回滞电压的区间需要控制在一定范围，否则就会使得输出整形信号的跳边沿不发生在信号的过零点出。