线性判别分析（二）——Bayes最优分类器的角度看LDA

线性判别分析（一）——LDA介绍
线性判别分析（二）——Bayes最优分类器的角度看LDA

在线性判别分析（一）——LDA介绍 一文中，我们介绍了LDA的基本思想、算法，但其实严格来讲博客中介绍的都是FDA。本文我们就来探究一下LDA的真面目。

1 Bayes准则

关于贝叶斯最优分类器的介绍请参考周志华的《机器学习》P147。对分类问题，在所有概率都已知的情况下，贝叶斯决策论考虑如何根据这些概率以及误判损失来选择最优类别标记。直接引入概念：

贝叶斯判定准则
为最小化总体风险，需要在每个样本上选择那个能使条件风险R(c|x) R(c|x) 最小的类别标记，即h^*(x)=\arg \min_{c\in {\cal Y}}R(c|x).

h∗(x)=argminc∈YR(c|x).

h∗ 称为贝叶斯最优分类器。

当学习目标是最小化分类错误率时，条件风险

R(c|x)=1−P(c|x),

于是贝叶斯最优分类器为

h∗(x)=argmaxc∈YP(c|x).

再利用贝叶斯定理得到

h∗(x)=argmaxc∈YP(c)P(x|c).(1)

这意味着，根据贝叶斯判定准则，对每个样本，我们需要选择使 P(c)P(x|c) 最大的类别。

机器学习的任务就是根据训练数据去估计概率分布 P(c|x) 或者 P(x,c) 。

2 LDA新视角

在LDA中，我们假设 P(x|c) 服从高斯分布，多变量高斯分布的密度函数为

fc(x)=1(2π)d/2|Σc|1/2e−12(x−μc)TΣ−1c(x−μc)(2)

其中d是实例x的维数， Σc 是协方差矩阵。并且假设所有类别对应的高斯分布的协方差矩阵相同，即

Σc=Σ(3)

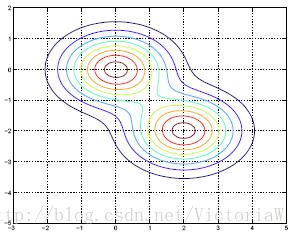
由于协方差矩阵决定着高斯分布的形状，所以在LDA中，所有类别的高斯分布形状相同，只是位置不同。下面是LDA模型概率分布的一个例子：

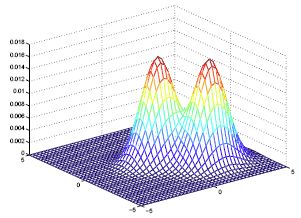
2.1 最优分类器

假设我们已经知道协方差矩阵 Σ ，后面会介绍一种估计 Σ 的方法。现在来看看贝叶斯最优分类器：

h∗(x)=arg maxcP(h=c|X=x)=arg maxcfc(x)P(c)=arg max c log(fc(x)P(c))=arg maxc[−log((2π)d/2|Σ|1/2)−12(x−μc)TΣ−1(x−μc)+log(P(c))]=arg maxc[−12(x−μc)TΣ−1(x−μc)+log(P(c))].(4)

其中，

−12(x−μc)TΣ−1(x−μc)=xTΣ−1μc−12μTcΣ−1μc−12xTΣ−1x.(5)

我们把(5)代回(4)中得到

h∗(x)= arg maxc[xTΣ−1μc−12μTcΣ−1μc+log(P(c))],(6)

这就是LDA的最优分类器。对于任意一个样本x，我们只需要把它代入上面的表达式，看哪个类别对应的值最大。

2.2 决策边界

记

δc(x)=xTΣ−1μc−12μTcΣ−1μc+log(P(c)),(7)

称为线性判别函数。

有

h∗(x)= arg maxcδc(x).(8)

于是类别k和类别l之间的决策边界为

{x:δk(x)=δl(x)}.(9)

也就是

logP(k)P(l)−12(μk+μl)TΣ−1(μk−μl)+xTΣ−1(μk−μl)=0,(10)

这是关于x的线性函数，对应超平面的法向量为

ω∗=Σ−1(μk−μl).(11)

所以LDA是一个线性分类器。

2.3 估计概率分布

现在我们需要根据训练数据估计 P(c) 以及高斯分布的参数。

2.3.1 P(c)

根据极大似然估计法，可以得到

P(c)=NcN,(12)

其中 Nc 是c类对应的训练样本数， N 是总训练样本数。

2.3.2 μc

用样本均值作为总体均值的估计：

μ^c=∑yi=cx(i)Nc.(13)

2.3.3 Σ

协方差矩阵 Σ 的估计稍微有点复杂，因为我们必须对所有的类别得到同一个协方差矩阵。

首先，对每个类别计算样本协方差矩阵，然后把所有类别的样本协方差矩阵相加，并用 N−C 进行归一化，得到

Σ^=1N−C∑c=1C∑yi=c(x(i)−μ^c)(x(i)−μ^c)T.(14)

其中 C 是类别数。极大似然估计法得到的协方差是用 N 进行归一化的，但是如果用 N−C 归一化，得到的是无偏估计。当训练样本数 N 非常大时， N−C 和 N 之间的差别非常小。

总结
如果想要用LDA算法进行分类，首先需要根据公式(12)(13)(14)估计参数，这其实就是训练过程。在预测时，根据公式(7)计算得到每个类别的判别值，取最大值对应类别作为预测结果。

3 LDA v.s. FDA

公式(11)对应LDA得到的分类超平面的法向量，是不是似曾相识？回忆一下FDA的投影方向:

ωFDA=S−1w(μ1−μ2).(15)

如果假设所有类别对应的协方差矩阵相同，那么有 Sw=2Σ ，此时 ω∗ 等价于 ωFDA .

那么问题来了，上面推导的LDA分类器和FDA分类器之间到底是啥关系呢？

LDA是在损失函数为分类错误率时，假设类内数据服从高斯分布并且协方差矩阵，得到的分类器。损失函数为分类错误率时，每个样本最优标记由（1）确定；而 P(x|c) 可以根据假设通过极大似然估计法确定。LDA认为好的分类器是能把实例划分到 P(c)P(x|c) 取值最大的类别的分类器（即分类错误率最小）。而FDA认为好的分类器是使得类内间距最小同时类间间距最大的投影方向对应的分类器。LDA和FDA有着不同的奋斗目标。但是在数据服从高斯分布且协方差矩阵相同时，FDA和LDA的目标一致了，他们得到的分类器是一样。所以LDA和FDA是萍水相逢的知己。

参考

[1] 9.2 - Discriminant Analysis