同步异步4：CDMA中的同步异步

除了在TDMA中存在同步异步的概念，在CDMA中也存在同步异步的概念，不过貌似这里的异步所指为一种对同步要求较低的情况。在《计算机网络 一种开源的设计实现方法》一书中对该同步异步区别进行了讲解。

首先CDMA是一种利用码元的正交性进行多路复用的方法，在CDMA中，每一个节点的数据都需要扩展成一个码元，比如说节点原来是需要发送1，现在需要发送1，1，-1，-1，在码元中，是采用+1，-1电平代表0,1的，同时，相较于原来一个周期发送一个符号1，现在则是发送一个码元1，1，-1，-1，从发送的频率上是增加了，故这也是同时包含扩频优势的方法。比如下图就是一个CDMA工作的示意图

在CDMA中的同步和异步主要体现在其选择的码元方式上的不同。简而言之，若采用正交码的模式则是同步CDMA，若采用PN序列的模式则是异步CDMA。

同步CDMA

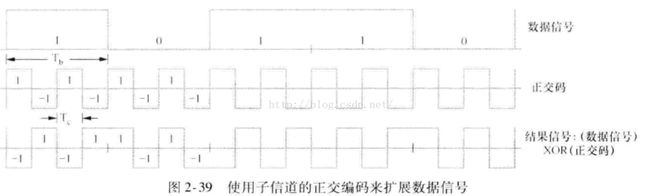
这里的正交码指的是绝对正交，比如沃什序列，故为了保持该绝对正交的特性，需要所有的符号之间达到完美的同步。正交码具有完美的互相关特性，即在一个正交码集合中，任意一对码元之间都是绝对正交的，不过对于自相关的特性，正交码并没有保证。貌似目前所有的编码方式中，都没有出现过自相关和互相关都完美的序列。在《计算机网络 一种开源的设计实现方法》一书中，同步CDMA的调制方法是采用XOR的方法的，如下图

不过貌似也可以把原始的数据信号直接和正交码矩阵做Kronecker积也行。绝对正交的码序列貌似也不多，且一般在通信上都是采用一阶的序列。高阶的正交序列包含U系统这些，不过由于其采用高阶图样，即类似模拟信号，从而对于同步性的要求更高，且生成较为复杂，目前在通信中没有看到应用。

异步CDMA

异步CDMA这里是所谓的采用PN序列的码元生成方式，按书上所述这是一种统计上的正交。首先为了更好的理解这种统计上的正交，我们需要对自相关和互相关有一个理解，自相关指同一个信号不同时刻进行相关计算，若信号的自相关性完美，比如barker码，该码也是802.11b 1M,2M速率所采用的扩频码，其具有完美的自相关特性，只有接受的信号顺序和码元完全对其时，其才有相关值，若偏离一位，其相关值则为-1，+1或者0。比如七位的barker码（这里貌似最好写成正负1的形式，在《计算机网络 一种开源的设计实现方法》一书中是写成1,0的形式，不太建议），1,1,1,-1,-1,1,-1，若码元对其的话，即1,1,1,-1,-1,1,-1时，相关值为7，否则若有一位移位的话，比如-1,1,1,1,-1,-1,1，则相关值只为-1。采用barker码，在没有多用户干扰的时候，能够避免同步所带来的额外要求，即对同步需求很低，故802.11的初始版本采用这种较为异步的方式。互相关是考虑一对码元之间的干扰的，如前面所述的正交码一样，若采用正交码，一对码元之间的互相关值为0，即其是不相关的。而这里书上所述的统计上的正交即是所谓取自相关特性和互相关特性的一个折中，在这里，正交即可以理解成，两个序列即是无关的，若序列越长，由于其无关，那么其互相关值则约等于0，从而其是正交的。比如采用扩频序列的方法可以抵抗噪声的干扰，从频域上理解是频谱更宽，从时域上理解就是扩频序列和噪声是无关的，从而其相关值接近0。在异步CDMA中，即采用设计过的PN序列，其序列除了与噪声无关，其任意两个序列之间也是接近无关的，从而可以认为是一种统计上的正交。不过采用特殊的异步CDMA的方法，可以达到一种自相关和互相关的折中，比如Gold序列，ZC根序列这些，同时可以根据该折中，调制序列的结构，从而更加灵活的设计符合工作环境的机制，比如用户多，还是同步性差的网络。有关异步CDMA的其他优势，按书中列举如下：