力扣高频|算法面试题汇总(五):链表
力扣高频|算法面试题汇总(一):开始之前
力扣高频|算法面试题汇总(二):字符串
力扣高频|算法面试题汇总(三):数组
力扣高频|算法面试题汇总(四):堆、栈与队列
力扣高频|算法面试题汇总(五):链表
力扣高频|算法面试题汇总(六):哈希与映射
力扣高频|算法面试题汇总(七):树
力扣高频|算法面试题汇总(八):排序与检索
力扣高频|算法面试题汇总(九):动态规划
力扣高频|算法面试题汇总(十):图论
力扣高频|算法面试题汇总(十一):数学&位运算
力扣高频|算法面试题汇总(五):链表
力扣链接
目录:
- 1.复制带随机指针的链表
- 2.环形链表
- 3.排序链表
- 4.相交链表
- 5.反转链表
- 6.回文链表
- 7.删除链表中的节点
- 8.奇偶链表
1.复制带随机指针的链表
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的 深拷贝。
我们用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
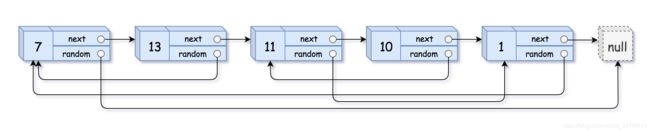
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
思路1:
回溯法。参考力扣官方
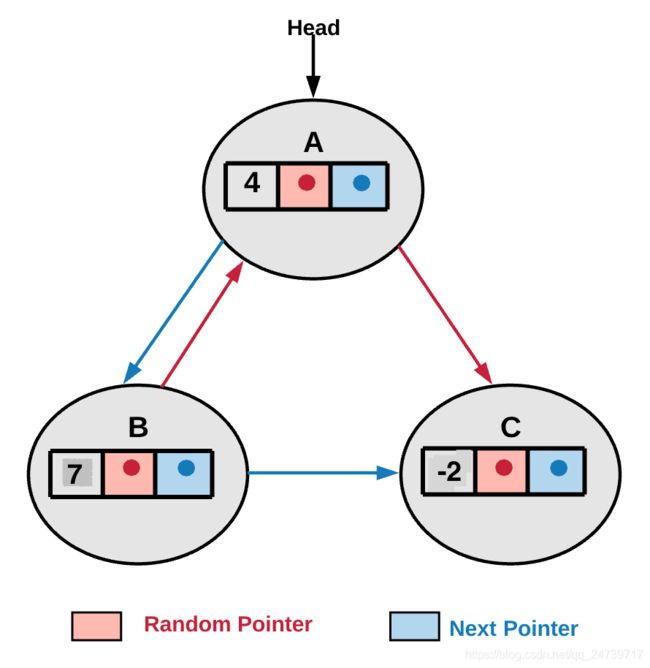
回溯算法的第一想法是将链表想象成一张图。链表中每个节点都有 2 个指针(next和random)。随机指针给图结构添加了随机性,所以我们可能会访问相同的节点多次,这样就形成了环。只需要遍历整个图并拷贝它。为例避免这种情况,需要用用一个字典记录是否遍历节点。步骤如下
- 1.从头指针开始遍历整个图。
- 2.当遍历到某个节点时判断是否经过这个节点,如果已经经过该节点则不需要拷贝。
- 3.如果没有经过这个节点,则进行拷贝。
- 4.分布对next和random指针进行回溯调用。
时间复杂度: O ( N ) O(N) O(N) ,其中 N 是链表中节点的数目。空间复杂度: O ( N ) O(N) O(N)。
C++
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
private:
// 字典将旧节点作为键,新节点作为其值
map<Node*, Node*> nodeHash;
public:
Node* copyRandomList(Node* head) {
if(!head)
return head;
// 回溯法先判断是否已经遍历
// 如果我们已经处理了当前节点,那么我们只需返回它的克隆版本
if(nodeHash.find(head) != nodeHash.end())
return nodeHash[head];
// 创建新的节点 值与旧节点相同
Node* node = new Node(head->val);;
// 添加到字典中
// 将此值保存在哈希图中。 这是必需的,
// 因为遍历过程中由于随机指针的随机性可能会出现循环,这将有助于我们避免循环。
nodeHash[head] = node;
// 递归寻找
// 以递归方式复制剩余的链表,从下一个指针开始,然后从随机指针开始。
// 因此,我们有两个独立的递归调用。
// 最后,我们为创建的新节点更新下一个和随机指针。
node->next = copyRandomList(head->next);
node->random = copyRandomList(head->random);
return node;
}
};/**/
Python
"""
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
"""
class Solution:
# 初始化节点字典
def __init__(self):
self.nodeHash = {
}
def copyRandomList(self, head: 'Node') -> 'Node':
if head == None:
return head
# 回溯的截止条件
if head in self.nodeHash:
return self.nodeHash[head]
# 拷贝节点
node = Node(head.val)
self.nodeHash[head] = node
node.next = self.copyRandomList(head.next)
node.random = self.copyRandomList(head.random)
return node
思路2:
O ( 1 ) O(1) O(1)空间的迭代。参考力扣官方
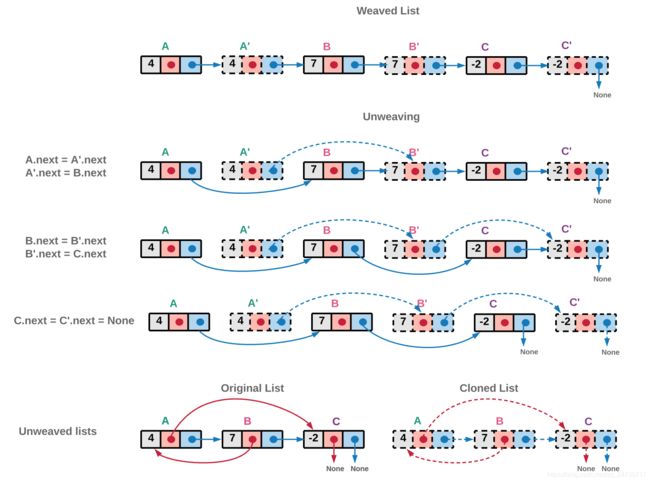
这个方法和剑指offer|解析和答案(C++/Python) (三):复杂链表的复制基本类似。算法分为三个步骤:
- 1.复制链表,即扩充原链表。
- 2.复制链表上链接随机节点。
- 3.复制链表和原链表断开,得到复制链表。
C++
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
Node* copyRandomList(Node* head) {
// 复制原链表节点
cloneNodes(head);
// 复制随机节点
cloneRandomNodes(head);
// 断开复制链表
return reconnectNodes(head);
}
void cloneNodes(Node* head){
Node* pNode = head;
while(pNode){
// 拷贝节点
Node* node = new Node(pNode->val);
node->next = pNode->next;
pNode->next = node;
// 移位
pNode = node->next;
}
}
void cloneRandomNodes(Node* head){
Node* pNode = head;
while(pNode){
// 随机节点链接
Node* node = pNode->next;
if(pNode->random){
// 如果原节点的随机链接不为空
node->random = pNode->random->next;
}
// 移位
pNode = node->next;
}
}
Node* reconnectNodes(Node* head){
Node* pCloneHead = NULL;
Node* pCloneNode = NULL;
Node* pNode = head;
// 获得原链表和复制链表的头指针
if(pNode){
pCloneHead = pNode->next;
pCloneNode = pCloneHead;
// 断开链接
pNode->next = pCloneNode->next;
// 移位
pNode = pNode->next;
}
// 拆开
while(pNode){
pCloneNode->next = pNode->next;
pCloneNode = pCloneNode->next;
// 断开链接
pNode->next = pCloneNode->next;
// 移位
pNode = pNode->next;
}
return pCloneHead;
}
};
Python:
"""
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
"""
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
self.cloneNodes(head)
self.cloneRandomNodes(head)
return self.reconnectNodes(head)
def cloneNodes(self, head):
pNode = head
while pNode:
# 拷贝
node = Node(pNode.val)
node.next = pNode.next
pNode.next = node
pNode = node.next
def cloneRandomNodes(self, head):
pNode = head
while pNode:
node = pNode.next
if pNode.random:
node.random = pNode.random.next
pNode = node.next
def reconnectNodes(self, head):
pCloneHead = None
pCloneNode = None
pNode = head
# 找头节点
if pNode:
pCloneHead = pNode.next
pCloneNode = pCloneHead
# 断开
pNode.next = pCloneNode.next
# 移位
pNode = pNode.next
while pNode:
pCloneNode.next = pNode.next
pCloneNode = pCloneNode.next
pNode.next = pCloneNode.next
pNode = pNode.next
return pCloneHead
2.环形链表
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例:
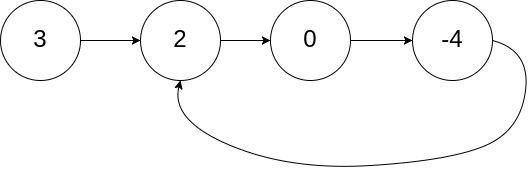
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
思路:
这道题是剑指offer|解析和答案(C++/Python) (二):链表中环的入口节点中的简单版,只需要考虑是否环存在。设置两个指针,一个快指针,一个慢指针,两个指针相遇则存在环,否则不存在。
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
// 两个指针,一个快指针,一个慢指针
ListNode* pSlow;
ListNode* pFast;
pSlow = head;
pFast = head;
while(pFast){
pSlow = pSlow->next;
pFast = pFast->next;
if(pFast)
pFast = pFast->next;
else
return false;
if(pFast == pSlow)
return true;
}
return false;
}
};
Python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: ListNode) -> bool:
if head == None:
return False;
pSlow = head
pFast = head
while pFast:
pSlow = pSlow.next
pFast = pFast.next
if pFast:
pFast = pFast.next
else:
return False
if pFast == pSlow:
return True
return False
3.排序链表
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
思路:
由于需要 O ( n l o g n ) O(n log n) O(nlogn) 时间复杂度,所以采用归并排序,由于常熟级空间复杂度,所以不能使用递归,得使用循环。参考图示:
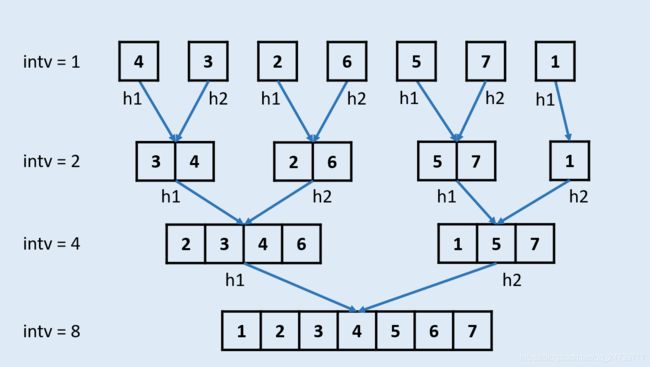
C++:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == NULL|| head->next ==NULL)
return head;
// 获取链表长度
ListNode* pNode = head;
int length = 0;
while (pNode) {
pNode = pNode->next;
++length;
}
ListNode* pRoot = new ListNode(0); /*新建根节点*/
pRoot->next = head; /*节点链接起来*/
int len = 1; /*设置每次归并的长度*/
while (len <length)
{
ListNode* pMerge = pRoot; /*合并的起始节点*/
ListNode* pNode = pRoot->next; /*移动的节点*/
while (pNode)
{
/*构建合并的链表h1*/
ListNode* pH1 = pNode;
int lH1 = len;
while (pNode != NULL && lH1 > 0) {
pNode = pNode->next;
--lH1;
}
if (lH1 > 0) /*如果h1不是完整长度,则说明没有h2*/
break; /*则无需合并h2*/
ListNode* pH2 = pNode;
int lH2 = len;
while (pNode != NULL && lH2 > 0) {
pNode = pNode->next;
--lH2;
}
int lenH1 = len;
int lenH2 = len - lH2; /*h2可能不是完整长度*/
while (lenH1 > 0 && lenH2 > 0)/*归并排序*/
{
/*链接子链表*/
if (pH1->val <= pH2->val) {
pMerge->next = pH1;
pH1 = pH1->next;
--lenH1;
}
else {
pMerge->next = pH2;
pH2 = pH2->next;
--lenH2;
}
pMerge = pMerge->next; /*移动*/
}
if (lenH1 > 0) {
/*h1链表还有剩余*/
pMerge->next = pH1;
while (lenH1)
{
pMerge = pMerge->next;/*不断移动pMerge*/
--lenH1;
}
}
else if (lenH2 > 0) {
pMerge->next = pH2;
while (lenH2)
{
pMerge = pMerge->next;
--lenH2;
}
}
pMerge->next = pNode; /*链接后面的部分*/
}
len = len * 2;
}
return pRoot->next;
}
};
Python:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def sortList(self, head: ListNode) -> ListNode:
if not head or head.next == None:
return head
# 获取链表的长度
pNode, length = head, 0
while pNode:
pNode, length = pNode.next, length + 1
# 新建根节点
pRoot = ListNode(0)
pRoot.next = head
l = 1 # 设置每次合并的规模
# 根据不同的链表切片规模,每一次都从头进行归并
while l < length :
# 合并的第一个节点、移动的节点
pMerge, pNode = pRoot, pRoot.next
# 根据当前的合并规模,将链表内的链表切片两两归并
while pNode: # 如果节点没有移动到最后时
# 获取当前需要归并的子链表h1
pH1, lH1 = pNode, l
# 不断移动pNode获得子链表
while lH1 and pNode:
pNode, lH1 = pNode.next, lH1 - 1
if lH1 > 0: # 没有获取完整长度的子链h1,说明没有h2,无需合并
break
# 获取当前需要归并的子链表h2
pH2, lH2 = pNode, l
# 不断移动pNode获得子链表
while lH2 and pNode:
pNode, lH2 = pNode.next, lH2 - 1
# 获取h1和h2链表的长度
lenH1, lenH2 = l, l - lH2 # lenH2长度可能比lenH1小
# 归并排序
while lenH1 and lenH2:
if pH1.val <= pH2.val:
pMerge.next = pH1
pH1 = pH1.next
lenH1 = lenH1 - 1
else:
pMerge.next = pH2
pH2 = pH2.next
lenH2 = lenH2 - 1
pMerge = pMerge.next
# 如果h1有剩余的
if lenH1 > 0:
pMerge.next = pH1 # 链接h1
while lenH1:
pMerge = pMerge.next # 移动pMerge
lenH1 -= 1
else:# 如果h2有剩余的
pMerge.next = pH2 # 链接h2
while lenH2:
pMerge = pMerge.next # 移动pMerge
lenH2 -= 1
# h1 和 h2 的归并只是影响了链表的一部分,
# 这里应该把归并后的链表切片跟原链表h2之后的部分拼起来
pMerge.next = pNode
# 得到新的合并规模
l *= 2
return pRoot.next
4.相交链表
编写一个程序,找到两个单链表相交的起始节点。
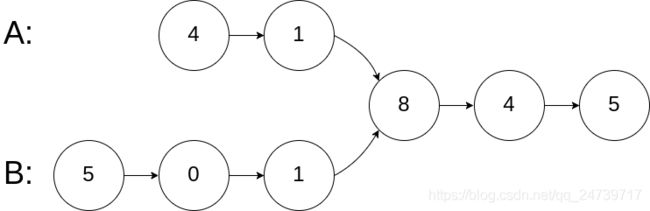
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
思路:
剑指offer有,可以看我以前写的博客:剑指offer|解析和答案(C++/Python) (四):两个链表的第一个公共节点
首先遍历两个链表得到两个链表的长度。第二次遍历的时候,在较长的链表上走若干步,接着同时在两个链表上进行遍历,找到第一个相同的节点便是第一个公共节点。这里不需要辅助栈,时间复杂度同样是 O ( m + n ) O(m+n) O(m+n)。
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
// 获取链表A的长度
int lengthA = 0;
ListNode * pNode = headA;
while(pNode){
pNode = pNode->next;
++lengthA;
}
// 获取链表B的长度
int lengthB = 0;
pNode = headB;
while(pNode){
pNode = pNode->next;
++lengthB;
}
ListNode * pNodeA = headA;
ListNode * pNodeB = headB;
int diff = lengthA - lengthB;
if(diff >= 0){
// A链表长,A先走
while(diff){
pNodeA = pNodeA->next;
--diff;
}
}else{
diff = -diff;
while(diff){
pNodeB = pNodeB->next;
--diff;
}
}
// 一起走找共同节点
while(pNodeA && pNodeB){
if(pNodeA == pNodeB){
return pNodeA;
}else{
pNodeA = pNodeA->next;
pNodeB = pNodeB->next;
}
}
return NULL;
}
};
Python:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
lengA = 0
lengB = 0
pNode = headA
while pNode:
pNode = pNode.next
lengA += 1
pNode = headB
while pNode:
pNode = pNode.next
lengB += 1
diff = lengA - lengB
pNodeA = headA
pNodeB = headB
if diff >= 0:
while diff:
pNodeA = pNodeA.next
diff -= 1
else:
diff = -diff
while diff:
pNodeB = pNodeB.next
diff -= 1
while pNodeA and pNodeB:
if pNodeA == pNodeB:
return pNodeA
pNodeA = pNodeA.next
pNodeB = pNodeB.next
return None
5.反转链表
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题?
思路:
这题在剑指offer做过,详见剑指offer|解析和答案(C++/Python) (二):反转链表。使用3个指针完成反转。
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL or head->next == NULL)
return head;
ListNode* pNode = head;
ListNode* pPre = NULL;
ListNode* pRever = NULL;
while(pNode->next){
pRever = pNode->next;
pNode->next = pPre;
pPre = pNode;
pNode = pRever;
}
pRever->next = pPre;
return pRever;
}
};
Python:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if head == None or head.next == None:
return head
pNode = head
pPre = None
pRever = None
while pNode.next:
pRever = pNode.next
pNode.next = pPre
pPre = pNode
pNode = pRever
pRever.next = pPre
return pRever
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL or head->next == NULL)
return head;
ListNode* p = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return p;
}
};
Python:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if head == None or head.next == None:
return head
pNode = self.reverseList(head.next)
head.next.next = head
head.next = None
return pNode
6.回文链表
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
思路:
使用快慢指针和栈实现。
空间复杂度 O ( n / 2 ) O(n/2) O(n/2)
- 快指针每次走两步,慢指针每次只走一步。
- 当快指针走到链表末尾时,慢指针刚好走到中间位置,从慢指针后面的链表开始压栈,再出栈依次和链表前部分比较。
(1)——>(2)——>(3)——>(2)——>(1)
slow fast
(1)——>(2)——>(3)——>(3)——>(2) ——> (1)
slow (fast) <strong>多走1步</strong> fast
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool isPalindrome(ListNode* head) {
if(head == NULL || head->next == NULL)
return true;
ListNode* pSlow;
ListNode* pFast;
pSlow = head;
pFast = head;
while(pFast->next && pFast->next->next){
pSlow = pSlow->next;
pFast = pFast->next->next;
}
// 将链表的后半段压入栈
stack<int> s;
while(pSlow->next){
s.push(pSlow->next->val);
pSlow = pSlow->next;
}
//依次比较前半部分元素和逆序的后半部分元素
while(!s.empty()){
if(s.top() == head->val){
s.pop();
head = head->next;
}else
return false;
}
return true;
}
};
Python:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
if not head or not head.next:
return True
pSlow = head
pFast = head
while pFast.next and pFast.next.next:
pSlow = pSlow.next
pFast = pFast.next.next
stack = []
while pSlow.next:
stack.append(pSlow.next.val)
pSlow = pSlow.next
while len(stack):
if stack[-1] == head.val:
head = head.next
stack.pop()
else:
return False
return True
思路2:
进阶,使用 O ( 1 ) O(1) O(1)空间复杂度。
和上一个思路的区别在于:最后不使用栈来倒序链表后半部分的元素,而是选择直接本地操作(额外空间复杂度为O(1)),在原链表上将后半部分元素倒置(反转),比较完后得出结果后,再 还原链表,返回结果。
C++
class Solution {
public:
bool isPalindrome(ListNode* head) {
if(head == NULL || head->next == NULL)
return true;
ListNode* pSlow;
ListNode* pFast;
pSlow = head;
pFast = head;
while(pFast->next && pFast->next->next){
pSlow = pSlow->next;
pFast = pFast->next->next;
}
//链表长度为偶数,fast指针最后多走一步到链表末尾
if(pFast->next)
pFast = pFast->next;
/*---------------区别----------------------*/
/*---------------链表后半部分倒序-----------*/
ListNode* p = pSlow->next;
ListNode* q = NULL;
ListNode* cur = NULL;
pSlow->next = NULL;
while(p){
cur = p->next;
p->next = q;
q = p;
p = cur;
}
while(1){
if(pFast->val != head->val){
// 不相等在不是
// 链表复原
ListNode* m = q->next;
ListNode* n = NULL;
ListNode* cur2 = NULL;
q->next = NULL;
while(m){
cur2 = m->next;
m->next = n;
n = m;
m = cur2;
}
pSlow->next = n;
return false;
}
//前、后一起往后移动
pFast = pFast->next;
head = head->next;
if(pFast == NULL)
break;
}
//链表复原
ListNode* m = q->next;
ListNode* n = NULL;
ListNode* cur2 = NULL;
q->next = NULL;
while(m){
cur2 = m->next;
m->next = n;
n = m;
m = cur2;
}
pSlow->next = n;
return true;
}
};
7.删除链表中的节点
请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点,你将只被给定要求被删除的节点。
示例:
输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
说明:
链表至少包含两个节点。
链表中所有节点的值都是唯一的。
给定的节点为非末尾节点并且一定是链表中的一个有效节点。
不要从你的函数中返回任何结果。
思路:
这题和从链表中删除节点有点不一样,因为那个会给你头节点,一直遍历到要删除的节点。但是这个直接给你要删除的节点,不知道前置节点的。思路如图所示:
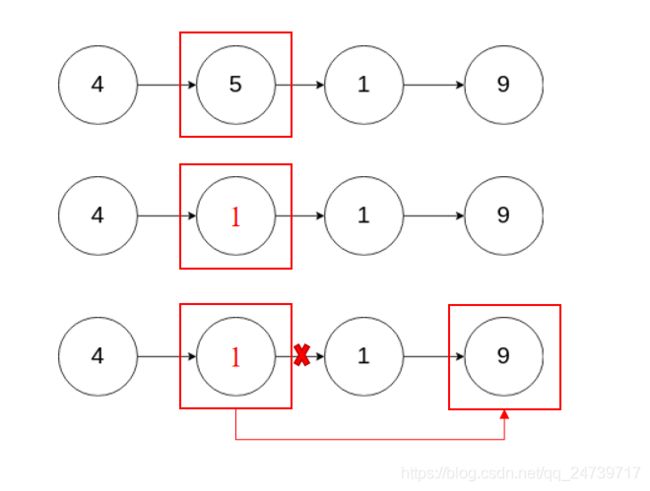
复制下一个节点的值,再链接下一个节点的下一个节点。
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
void deleteNode(ListNode* node) {
node->val = node->next->val;
node->next = node->next->next;
}
};
Python:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def deleteNode(self, node):
"""
:type node: ListNode
:rtype: void Do not return anything, modify node in-place instead.
"""
node.val = node.next.val
node.next = node.next.next
8.奇偶链表
给定一个单链表,把所有的奇数节点和偶数节点分别排在一起。请注意,这里的奇数节点和偶数节点指的是节点编号的奇偶性,而不是节点的值的奇偶性。
请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1),时间复杂度应为 O(nodes),nodes 为节点总数。
示例 1:
输入: 1->2->3->4->5->NULL
输出: 1->3->5->2->4->NULL
说明:
应当保持奇数节点和偶数节点的相对顺序。
链表的第一个节点视为奇数节点,第二个节点视为偶数节点,以此类推。
思路:
使用两个指针,分别用来链接奇数节点和偶数节点。在链接完之后,这个链表被拆分程两个部分:奇数节点子链表和偶数节点子链表,因此最后一步就是把两个链表链接起来。
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
if(head == NULL || head->next==NULL)
return head;
ListNode* pOdd = head;
ListNode* pEven = head->next;
ListNode* pEvenHead = pEven;
while(pOdd->next && pEven->next){
// 链接
pOdd->next = pEven->next;
// 移位
pOdd = pOdd->next;
pEven->next = pOdd->next;
pEven = pEven->next;
}
// 链接奇偶链
pOdd->next = pEvenHead;
return head;
}
};
Python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def oddEvenList(self, head: ListNode) -> ListNode:
if not head or not head.next:
return head
pOdd = head
pEven = head.next
pEvenHead = pEven
while pOdd.next and pEven.next:
pOdd.next = pEven.next
pOdd = pOdd.next
pEven.next = pOdd.next
pEven = pEven.next
pOdd.next = pEvenHead
return head