二分图的判定（C语言）

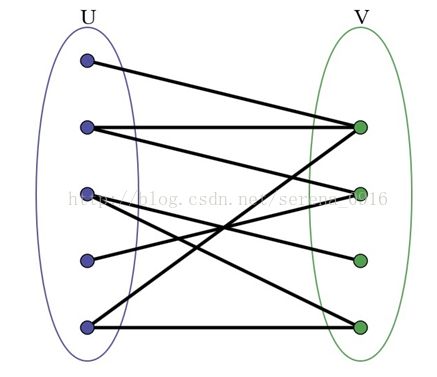
二分图又称为二部图，其定义是：设G=(V,E)是一个无向图。如顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。也就是说在二分图中，顶点可以分为两个集合X和Y，每一条边的两个顶点都分别位于X和Y集合中。它满足这样一个特性，即有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中，每个顶点集中没有边相连接！如下图所示：

无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。

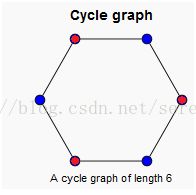这是一个二分图，所有相邻顶点颜色不同（使用颜色区分只是为了好表达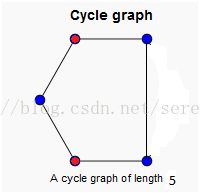）。这不是一个二分图，存在相邻顶点颜色相同的情况，且我们发现它的回路长度为奇数。因此，可以推出如果一个图存在奇圈（长度为奇数的回路），则它一定不是二分图。

判定一个图是否是二分图比较简单，可以使用 BFS解决。算法过程为：借助队列，进行宽度优先遍历，先对一个起点着色RED，然后将其所有相邻的节点着色为BLUE，并加入队列。只要能保证相邻的节点是不同的颜色即可。

#include
#include
#define Vexnum 100
int isBipartite(int map1[][Vexnum],int n);
int map1[Vexnum][Vexnum]={0};
struct QueueSq{
    int  *queue1;
    int  front1;
    int  rear;
    int MaxSize;
  } ;


void InitQueue(struct QueueSq* Q, int ms)
{ if(ms<=0) {printf("ms值非法!\n"); exit(1);}
Q->MaxSize=ms;
Q->queue1=(int *)malloc(ms*sizeof(int));
if(!Q->queue1) {
       printf("内存空间用完!\n");
   exit(1);
       }
Q->front1=Q->rear=0;
        }
void EnQueue(struct QueueSq* Q, int x)
   {
     /*当队列满时进行动态重分配*/
     if((Q->rear+1)%Q->MaxSize==Q->front1)
         /*againMalloc(Q)*/;
     /*求出队尾的下一个位置*/
 Q->rear=(Q->rear+1)%Q->MaxSize;
 /*把item的值赋给新的队尾位置*/
  Q->queue1[Q->rear]=x;
    }
int OutQueue(struct QueueSq* Q)
{   /*若队列为空则终止运行*/
 if(Q->front1==Q->rear) {
printf("队列已空，无法删除!\n");
exit(1);}
  /*使队首指针指向下一个位置*/
  Q->front1=(Q->front1+1)%Q->MaxSize;
  /*返回队首元素*/
  return Q->queue1[Q->front1];
 }
 void ClearQueue(struct QueueSq *Q)
 {
if (Q->queue1!=NULL)
free(Q->queue1);
Q->queue1=0;
Q->front1=Q->rear=0;
Q->MaxSize=0;
}
int EmptyQueue(struct QueueSq *Q)
{
if (Q->front1==Q->rear)
return 1;
else
return 0;
}
int PeekQueue(struct QueueSq *Q)
 {
if (Q->front1==Q->rear)
{ printf("queue is empty!\n");
      exit(1);
}
return Q->queue1[(Q->front1+1)%Q->MaxSize];
}


int main(int argc, char *argv[])
{
int N,M,v,e;
scanf("%d%d",&N,&M);  /*输入无向图的顶点数和边数*/
    for (int i = 0; i < M; i++)
    {
        scanf("%d%d",&v,&e);
        map1[v][e] = 1;   /* 使用邻接矩阵保留图的信息*/
    }
if(!isBipartite(map1,N))
{
printf("该图不是二分图");
}
else
{
printf("该图是二分图");
}


}


int isBipartite(int map1[][Vexnum],int n) {
//colorArr[i] 代表第i个结点的颜色
int colorArr[Vexnum] = {0};
colorArr[0] = 1;
struct QueueSq queue1;
InitQueue(&queue1,n);
EnQueue(&queue1,0);
while(!EmptyQueue(&queue1)){
int top =OutQueue(&queue1);
for(int i=0; iif(map1[top][i] == 1 && colorArr[i] == 0){
colorArr[i] = 3 - colorArr[top];//两种颜色 1和2 交替着色
EnQueue(&queue1,i);
}else if(map1[top][i] == 1 &&  colorArr[i] == colorArr[top] ){
return 0;
}
}
}
return 1;
}

代码是完整的，已通过测试。顶点从0开始哈。