惹某der自闭集训第5周学习摘录（习题+感悟）

（一）课堂内容

快速排序

#include 
#include 
using namespace std;
//对数组a的元素[l,r)进行快速排序 ，用临时空间，取首快排 
void QuickSort(int *a, int l, int r);
//对数组a的元素[l,r)进行快速排序 ，不用临时空间，取尾快排 
void QuickSort2(int *a, int l, int r);


int main()
{
     
	int a[] = {
     30,38,3,32,15,1,41,47,59,80,6,93,78,18,65,60,51,22};
//	int a[] = {5,2,8,3,4};
	int n = sizeof(a) / sizeof(*a);
	QuickSort(a,0,n);	
//	QuickSort2(a,0,n);
	for(int i = 0;i < n;i++)
		cout << a[i] << " ";
	cout << endl;
	return 0;
}

//对数组a的元素[l,r)进行快速排序 ，取尾快排 
void QuickSort2(int *a, int l, int r)
{
     
	//递归终止条件
	if(l >= r)	
		return;	
	int t = r - 1;		//取尾快排 
	int p = l;			//分区点
	for(int j = l;j < r - 1;j++){
     
		if(a[j] < a[t]){
     //如果 
//			cout << " 交换" << endl; 
			swap(a[p],a[j]);
			p++;
		}
	}
//	cout << p << endl; 
	swap(a[p],a[t]);	
	QuickSort2(a,l,p);		//左边快排 
	QuickSort2(a,p + 1,r);	//右边快排，不包括参照元素 
} 

//对数组a的元素[l,r)进行快速排序 ，取首快排 
void QuickSort(int *a, int l, int r)
{
     
	//递归终止条件
	if(l >= r)	
		return;
	//按最坏可能，为两个子数组分配空间new
//	int *left = (int *)mallo((r - l) * sizeof(int));
	int *left = new int[r - l];
	int *right = new int[r - l];
	//设置两个子数组长度的初值为0
	int nl = 0,nr = 0;
	//1.拆分，左半部分都比参照元素小
	int t = a[l];	//取第一个元素作为参照元素 
	for(int i = l + 1;i < r;i++){
     
		if(a[i] <= t){
     
			left[nl] = a[i];
			nl++;
		} 
		//右半部分都比参照元素大
		else
			right[nr++] = a[i];		
	}
	//2.对子数组进行排序，递归调用 
	QuickSort(left,0,nl);
	QuickSort(right,0,nr);
	//3.合并子数组
	for(int i = 0;i < nl;i++)	
		a[l + i] = left[i];
	a[l + nl] = t;
	for(int i = 0;i < nr;i++)
		a[l + nl + 1 + i] = right[i];
	//4.释放空间 
// 	free(left);
	delete[] left;
	delete[] right;
} 

经典例题：兔子问题

题目描述

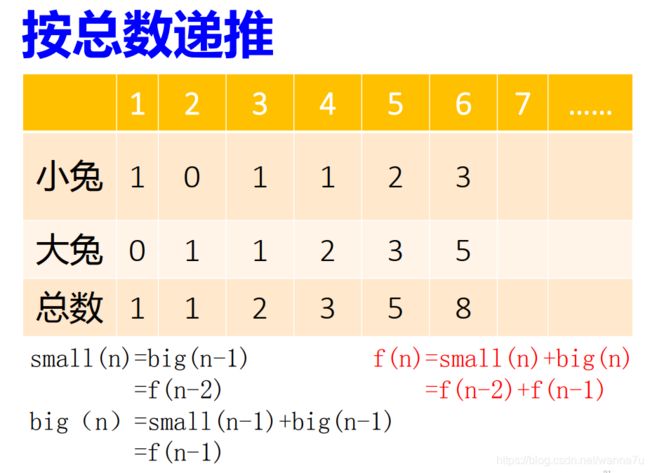
假设一对初生兔子要一个月才到成熟期，而一对成熟兔子每月会生一对兔子，那么，由一对初生兔子开始，12 个月后会有多少对兔子呢？

理解

AC代码

#include 
using namespace std;

int main(){
     
	int n;
	cin >> n;
	if(n == 1){
     
		cout << 1 << endl;
		return 0;
	}
	int a = 1,b = 1;
	for(int i = 2;i < n;i++){
     
		a = a + b;
		int c = a;
		a = b;
		b = c;
	}
	cout << b << endl;
	return 0;
}

折线分割平面 （2050）

题目描述

平面上有n条折线，问这些折线最多能将平面分割成多少块?

Sample Input

1
2

Sample Output

2
7

理解

过河卒

题目描述

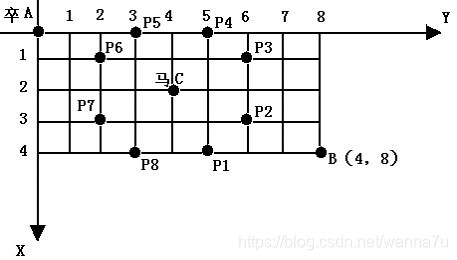
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m)(n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

Input

键盘输入B点的坐标（n,m）以及对方马的坐标（X,Y），不用判错。

Output

屏幕输出一个整数（路径的条数）。

Sample Input

4 8 2 4

Sample Output

0

理解

当不考虑马的控制点的时候路径的递推式为：F[i][j]= F[i-1][j]+F[i][j-1]，边界条件为F[0][0]=1
大佬的方法：只需要标记马的控制点。用两个一维数组来表示马的横向位移和纵向位移，这样来方便我们计算马的控制点，然后使用一个二维数组来标记某个点是否是马控制的点。

惹某的AC代码

#include 
using namespace std;
 
int main(){
     
    int ex,ey,x,y;
    scanf("%d %d %d %d",&ex,&ey,&x,&y);
    long long a[25][25];
    for(int i = 0;i < 25;i++)
        for(int j = 0;j < 25;j++)
            a[i][j] = 1;
    a[x][y] = 0,a[x+1][y+2] = 0,a[x+2][y+1] = 0;
    if(x >= 1) a[x-1][y+2] = 0;
    if(x >= 2) a[x-2][y+1] = 0;
    if(y >= 1) a[x+2][y-1] = 0;
    if(y >= 2) a[x+1][y-2] = 0;
    if(x>=2&&y>=1) a[x-2][y-1] = 0;
    if(y>=2&&x>=1) a[x-1][y-2] = 0;
//  for(int i = 0;i<= ex;i++){
     
//      for(int j = 0;j <= ey;j++){
     
//          cout << a[i][j] << " ";
//      }
//      cout << endl;
//  }
//  cout << endl;
    for(int i = 0;i <= ex;i++){
     
        for(int j = 0;j <= ey;j++){
     
            if(!a[i][j]) continue;
            if(i == 0 && j == 0) continue;
            else if(i == 0) a[i][j] = a[i][j-1];
            else if(j == 0) a[i][j] = a[i-1][j];
            else a[i][j] = a[i-1][j] + a[i][j-1];
        }
    }
//  for(int i = 0;i<= ex;i++){
     
//      for(int j = 0;j <= ey;j++){
     
//          cout << a[i][j] << " ";
//      }
//      cout << endl;
//  }
    cout << a[ex][ey] << endl;
    return 0;
}

大佬的部分代码

int cx, cy; //马的坐标
int x[8] = {
     1, 1, 2, 2, -1, -1, -2, -2}; //横向位移
int y[8] = {
     2, -2, 1, -1, 2, -2, 1, -1}; //纵向位移
int d[30][30]; //用来记录是否是马控制点
for (int i = 0; i < 30; ++i) {
      //将 d 数组初始化为 0
for (int j = 0;j < 30; ++j)
d[i][j] = 0;
}
d[cx][cy] = 1; // 用 1 来表示该点为马控制点
for (int i = 0; i < 8; ++i) {
     
int tx = cx + x[i]; //计算马控制点横坐标
int ty = cy + y[i]; //计算马控制点纵坐标
if (tx >= 0 && tx <= n && ty >= 0 && ty <= n)
d[tx][ty] = 1; //记录为马控制点
}

背包

0/1背包问题-二维数组

0/1背包问题-滚动数组

完全背包

有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是w[i]，价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

理解

类似于01背包问题，所不同的是每种物品有无限件。也就是从每种物品的角度考虑，与它相关的策略已并非取或不取两种，而是有取0件、取1件、取2件……等很多种，像
f[i][v] = max ( f[i-1][v-kw[i]]+kc[i] (0<=k*w[i] <= v)

【问题描述】

设有n种物品，每种物品有一个重量及一个价值。但每种物品的数量是无限的，同时有一个背包，最大载重量为M，今从n种物品中选取若干件(同一种物品可以多次选取)，使其重量的和小于等于M，而价值的和为最大。

【输入格式】

第一行：两个整数，M(背包容量，M<=200)和N(物品数量，N<=30)；
第2…N+1行：每行二个整数Wi,Ci，表示每个物品的重量和价值。

【输出格式】

仅一行，一个数，表示最大总价值。

【样例输入】

10 4
2 1
3 3
4 5
7 9

【样例输出】

max=12

AC代码-解法一

#include
using namespace std;
const int maxm = 201, maxn = 31;
int m, n;
int w[maxn], c[maxn];
int f[maxn][maxm];
int main(){
     
	scanf("%d%d",&m, &n); //背包容量m和物品数量n
	for (int i = 1; i <= n; i++)
		scanf(“%d%d”,&w[i],&c[i]); //每个物品的重量和价值
	for (int i = 1; i <= n; i++) //f[i][v]表示前i件物品，总重量不超过v的最优价值
		for (int v = 1; v <= m; v++)
			if (v < w[i]) f[i][v] = f[i-1][v];
			else
				if (f[i-1][v] > f[i][v-w[i]]+c[i]) f[i][v] = f[i-1][v];
				else f[i][v] = f[i][v-w[i]]+c[i];
	printf("max=%d",f[n][m]); // f[n][m]为最优解
	return 0;
}

AC代码-解法二

#include
using namespace std;
const int maxm=2001,maxn=31;
int main(){
     
	int n,m,v,i;
	int c[maxn],w[maxn];
	int f[maxm];
	scanf("%d%d",&m,&n); //背包容量m和物品数量n
	for(i=1;i<=n;i++) scanf("%d%d",&w[i],&c[i]);
	for(i=1;i<=n;i++)
		for(v=w[i];v<=m;v++) //设 f[v]表示重量不超过v公斤的最大价值
			f[v]=max(f[v],f[v-w[i]]+c[i]);
	printf("max=%d\n",f[m]); // f[m]为最优解
	return 0;
}

多重背包问题

这题目和完全背包问题很类似。令f[i][v]表示前i种物品恰放入一个容量为v的背包的最大权值，则：f[i][v]=max{f[i-1][v-kw[i]]+kc[i]|0<=k<=n[i]}。

例题：庆功会

为了庆贺班级在校运动会上取得全校第一名成绩，班主任决定开一场庆功会，为此拨款购买奖品犒劳运动员。期望拨款金额能购买最大价值的奖品，可以补充他们的精力和体力。

Input

第一行二个数n(n<=500)，m(m<=6000)，其中n代表希望购买的奖品的种数，m表示拨款金额。
接下来n行，每行3个数，v、w、s，分别表示第I种奖品的价格、价值（价格与价值是不同的概念）和购买的数量（买0件到s件均可），其中v<=100，w<=1000，s<=10。

Output

第一行：一个数，表示此次购买能获得的最大的价值（注意！不是价格）。

Sample Input

5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1

Sample Output

1040

AC代码-朴素算法

#include
using namespace std;
int v[6002], w[6002], s[6002];
int f[6002];
int n, m;
int max(int x,int y){
     
	if (x < y) return y;
	else return x;
}
int main(){
     
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i++)
		scanf("%d%d%d",&v[i],&w[i],&s[i]);
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= 0; j--)
			for (int k = 0; k <= s[i]; k++){
     
				if (j-k*v[i]<0) break;
				f[j] = max(f[j],f[j-k*v[i]]+k*w[i]);
			}
	printf("%d",f[m]);
	return 0;
}

AC代码-二进制优化，转换为01背包

#include
int v[10001],w[10001];
int f[6001];
int n,m,n1;
int max(int a,int b){
     
	//这句话等于：if (a>b) return a; else return b;
	return a>b?a:b; 
}
int main(){
     
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
     
		int x,y,s,t=1;
		scanf("%d%d%d",&x,&y,&s);
		while (s>=t) {
     
			v[++n1]=x*t; //相当于n1++; v[n1]=x*t;
			w[n1]=y*t;
			s-=t;
			t*=2;
		}
		v[++n1]=x*s;
		w[n1]=y*s; //把s以2的指数分堆：1，2，4，…，2^(k-1)，s-2^k+1,
	}
	for(int i=1;i<=n1;i++)
		for(int j=m;j>=v[i];j--)
			f[j]=max(f[j],f[j-v[i]]+w[i]);
	printf("%d\n",f[m]);
	return 0;
}

混合背包问题

例题

一个旅行者有一个最多能用V公斤的背包，现在有n件物品，它们的重量分别是W1，W2，…,Wn,它们的价值分别为C1,C2,…,Cn。有的物品只可以取一次（01背包），有的物品可以取无限次(完全背包），有的物品可以取的次数有一个上限（多重背包）。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

Input

第一行：二个整数，V(背包容量，V<=200)，N(物品数量，N<=30)；
第2…N+1行：每行三个整数Wi,Ci,Pi，前两个整数分别表示每个物品的重量，价值，第三个整数若为0，则说明此物品可以购买无数件，若为其他数字，则为此物品可购买的最多件数(Pi)。

Output

仅一行，一个数，表示最大总价值

Sample Input

10 3
2 1 0
3 3 1
4 5 4

Sample Output

11

AC代码-二进制优化，转换为01背包

#include
using namespace std;
int m, n;
int w[31], c[31], p[31];
int f[201];
int main(){
     
	scanf("%d%d",&m,&n);
	for (int i = 1; i <= n; i++)
		scanf("%d%d%d",&w[i],&c[i],&p[i]);
	for (int i = 1; i <= n; i++)
		if (p[i] == 0) {
      //完全背包
		for (int j = w[i]; j <= m; j++)
			f[j] = max(f[j], f[j-w[i]]+c[i]);
		}
		else {
     
			for (int j = 1; j <= p[i]; j++) //01背包和多重背包
				for (int k = m; k >= w[i]; k--)
					f[k] = max(f[k],f[k-w[i]]+c[i]);
		}
	printf("%d",f[m]);
	return 0;
}

（二）有趣的题目

A - Fishing Master

ccpc网络赛的贪心自闭题是也（我菜我自闭）

题目描述

    Heard that eom is a fishing MASTER, you want to acknowledge him as your mentor. As everybody knows, if you want to be a MASTER’s apprentice, you should pass the trial. So when you find fishing MASTER eom, the trial is as follow:
    There are n fish in the pool. For the i - th fish, it takes at least ti minutes to stew(overcook is acceptable). To simplify this problem, the time spent catching a fish is k minutes. You can catch fish one at a time and because there is only one pot, only one fish can be stewed in the pot at a time. While you are catching a fish, you can not put a raw fish you have caught into the pot, that means if you begin to catch a fish, you can’t stop until after k minutes; when you are not catching fish, you can take a cooked fish (stewed for no less than ti) out of the pot or put a raw fish into the pot, these two operations take no time. Note that if the fish stewed in the pot is not stewed for enough time, you cannot take it out, but you can go to catch another fish or just wait for a while doing nothing until it is sufficiently stewed.
    Now eom wants you to catch and stew all the fish as soon as possible (you definitely know that a fish can be eaten only after sufficiently stewed), so that he can have a satisfying meal. If you can complete that in the shortest possible time, eom will accept you as his apprentice and say “I am done! I am full!”. If you can’t, eom will not accept you and say “You are done! You are fool!”.
    So what’s the shortest time to pass the trial if you arrange the time optimally?

Input

    The first line of input consists of a single integer T(1≤T≤20), denoting the number of test cases.
    For each test case, the first line contains two integers n(1≤n≤105),k(1≤k≤109), denoting the number of fish in the pool and the time needed to catch a fish.
    the second line contains n integers, t1,t2,…,tn(1≤ti≤109) ,denoting the least time needed to cook the i - th fish.

Output

    For each test case, print a single integer in one line, denoting the shortest time to pass the trial.

Sample Input

2
3 5
5 5 8
2 4
3 3

Sample Output

23
11

理解

对于这道题，比赛看到时，和队友理解的第一思路就是贪心。不过我当时贪心的想法错了，我原来是想抓鱼的时间不能省，在抓鱼的时候同时煮鱼，使得时间最少，然鹅实践代码不太对头。
后来结束后听了大佬们的想法，发现也没有那么难，就是煮鱼的时间是不能省的，然后在煮鱼的同时尽可能的能抓几条就是几条。
因为抓鱼时间固定，所以讲每次多余的时间从多到少排序，然后按顺序在每次加入多抓鱼需要的时间ain可以使得时间最少。

下面是题目对样例的一些分析，最起先误导了我以为贪心先贪煮的时间久的鱼（这就很自闭）
Hint：
Case 1: Catch the 3rd fish (5 mins), put the 3rd fish in, catch the 1st fish (5 mins), wait (3 mins),
take the 3rd fish out, put the 1st fish in, catch the 2nd fish(5 mins),
take the 1st fish out, put the 2nd fish in, wait (5 mins), take the 2nd fish out.
Case 2: Catch the 1st fish (4 mins), put the 1st fish in, catch the 2nd fish (4 mins),
take the 1st fish out, put the 2nd fish in, wait (3 mins), take the 2nd fish out.

AC代码

#include 
using namespace std;
typedef long long ll;
bool cmp(ll a,ll b){
     
	return a > b;
}
int main(){
     
	ll t;
	scanf("%lld",&t);
	while(t--){
     
		ll n,k;
		ll sum = 0;
		scanf("%lld %lld",&n,&k);
		sum += k;
		ll a[n];
		for(int i = 0;i < n;i++){
     
			scanf("%lld",&a[i]);
			sum += a[i];
		}
		ll left = n - 1;
		for(int i = 0;i < n;i++){
     
			if(a[i] > k){
     
				left -= a[i]/k;
				a[i] %= k;
			}
		}
		if(left <= 0) cout << sum << endl;
		else{
     
			sort(a,a+n,cmp);
			for(int i = 0;i < left;i++){
     
				sum += k - a[i];
			}
			cout << sum << endl;
		}
	} 
	return 0;
} 

B - 位数问题

题目描述

     在所有的N位数中，有多少个数中有偶数个数字3？由于结果可能很大，你只需要输出这个答案对12345取余的值。

Input

    读入一个数n（1≤n≤1000）

Output

    输出有多少个数中有偶数个数字3。

Sample Input

2

Sample Output

73

理解

这题其实不难，but有个点卡了我很久，因为我没有好好读题，我把0也算作了1位数字中包含偶数个3的数字
这就很尴尬了，前面一错步步错，所以要读题！读题啊姐妹们

提示：
在所有的2位数字，包含0个3的数有72个，包含2个3的数有1个，共73个

AC代码

#include 
using namespace std;
const int N = 12345;
int a[1005]={
     0},b[1005]={
     0};
int main(){
     
    int n;
    scanf("%d",&n);
    a[1] = 1,b[1] = 8;
    for(int i = 2;i <= n;i++){
     
        a[i] = (b[i-1]+a[i-1]*9)%N;
        b[i] = (a[i-1]+b[i-1]*9)%N;
    }
    printf("%d\n",b[n]);
    return 0;
}

C - 蜜蜂路线

题目描述

     一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房M开始爬到蜂房N，M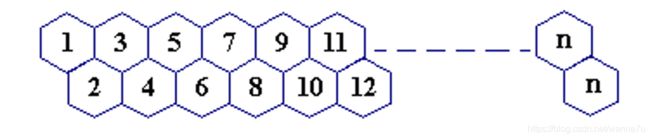

Input

    输入M，N的值，已知M

Output

    爬行有多少种路线。

Sample Input

1 14

Sample Output

377

理解

乍一看题目很简单，然后快速地打完代码上交，诶WA了，错在高精度。
在大佬的指点下（通过上周的麦森数已经对高精度压位操作有了些许了解），把数据存到数组中。

惹某的AC代码

#include 
using namespace std;
int sum[1005],a[1005],b[1005];
void func(){
     
    int i,j;
    for(i = 1,j = 1;i <= a[0] || j <= b[0];i++,j++){
     
        sum[i] = a[i] + b[i];
    }
    for(int i = 1;i <= sum[0];i++){
     
        sum[i+1] += sum[i] / 10;
        sum[i] %= 10;
    }
    if(sum[i]) sum[0]++;
    return;
}
void mov(){
     
    a[0] = b[0];
    for(int i = 1;i <= a[0];i++) a[i] = b[i];
    b[0] = sum[0];
    for(int i = 1;i <= b[0];i++) b[i] = sum[i];
}
int main(){
     
    int m,n;
    cin >> m >> n;
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    memset(sum,0,sizeof(sum));
    a[0] = a[1] = b[0] = b[1] = sum[0] = sum[1] = 1;
    for(int i = m + 2;i <= n;i++){
     
        func();
        mov();
    }
    for(int i = sum[0];i >= 1;i--) cout << sum[i];
    cout << endl;
    return 0;
}

大佬的AC代码

源代码地址：https://www.cnblogs.com/lyqlyq/p/6598772.html

#include
#include
using namespace std;
int main()
{
     
    __int64  f[60];
    int a,b,c;
    scanf("%d %d",&a,&b);
        f[a]=0;//将a的初值赋值为0； 
        f[a+1]=1;//下一步赋值为1； 
        f[a+2]=2;//赋值为2； 
        if(b-a==1)//若a==b,cout<<1; 
            printf("1\n");
        else
        {
     
           for(int i=a+3;i<=b;i++)
               f[i]=f[i-1]+f[i-2];//第i个=前两个之和； 
           printf("%d\n",f[b]);
        }
    return 0;
}

D - 邮票问题

题目描述

    设有已知面额的邮票m种，每种有n张，用总数不超过n张的邮票，能从面额1开始，最多连续组成多少面额。（1≤m≤100，1≤n≤100，1≤邮票面额≤255）

Input

    第一行：m,n的值，中间用一空格隔开。
    第二行：A[1…m]（面额），每个数中间用一空格隔开。

Output

    连续面额数的最大值

Sample Input

3 4
1 2 4

Sample Output

14

理解

注意题目说面额从1开始连续，所以最起先记得判定一下1有没有，若没有则直接输出0

AC代码

#include 
using namespace std;
 
int main(){
     
    int m,n;
    cin >> m >> n;
    int a[10005];
    int b[10005];
    for(int i = 0;i < m;i++) cin >> a[i];
    sort(a,a+m);
    if(a[0] != 1){
      //第一张不是1 
        cout << 0 << endl;
        return 0;
    }
    b[0] = 0;
    for(int i = 1;;i++){
     
        b[i] = 0x3f3f3f3f;
        for(int j = 0;j < m && a[j] <= i;j++){
     
            b[i] = min(b[i],b[i - a[j]] + 1);
        }
        if(b[i] == 0x3f3f3f3f || b[i] > n){
     
            cout << i - 1 << endl;
            break;
        }
    }
    return 0;
}

E - 最大子阵和

题目描述

    有一个包含正数和负数的二维数组。一个子矩阵是指在该二维数组里，任意相邻的下标是1*1或更大的子数组。一个子矩阵的和是指该子矩阵中所有元素的和。本题中，把具有最大和的子矩阵称为最大子矩阵。
例如：
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
这个数组的最大子矩阵为：
9 2
-4 1
-1 8
其和为15。

Input

    输入包含多组测试数据。每组输入的第一行是一个正整数N（1<=N<=100），表示二维方阵的大小。接下来N行每行输入N个整数，表示数组元素，范围为[-127，127]。

Output

    输出最大子阵和。

Sample Input

4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

Sample Output

15

理解

算水题吧毕竟是暴力过的，就循环一个开头（表示从第几行开始）和一个结尾（表示到第几行结束）
然后自定义函数判断取几列值更大，就没了安...也不知道自己当初咋就wa了呢

AC代码

#include
using namespace std;
const int N = 1000 + 5;
 
int maxx(int ans[],int n){
     
    int sum = 0,maxm = -0x3f3f3f3f;
    for(int i = 1;i <= n;i++){
     
        sum += ans[i];
        if(sum > maxm) maxm = sum;
        if(sum < 0) sum = 0;
    }
    return maxm;
}
int main(){
     
    int n;
    while(cin >> n){
     
        int a[N][N]={
     0};
        int ans[N]={
     0};
        int maxn = -0x3f3f3f3f;
        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= n;j++)
                cin >> a[i][j];
        for(int i = 1;i <= n;i++){
      //从第几行开始 
            memset(ans,0,sizeof(ans));
            for(int j = i;j <= n;j++){
     
                for(int k = 1;k <= n;k++){
     
                    ans[k] += a[j][k];
                }
//              for(int k = 1;k <= n;k++)
//                  cout << ans[k] << " ";
//              cout << endl << endl;
                int t = maxx(ans,n);
                if(t > maxn) maxn = t;
            }
        }
        cout << maxn << endl;
    }
    return 0;
}

F - 最短路径

题目描述

    下图表示城市之间的交通路网，线段上的数字表示费用，单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。

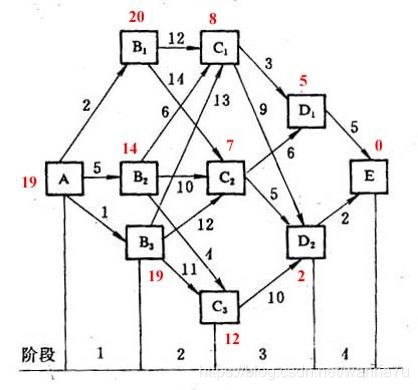
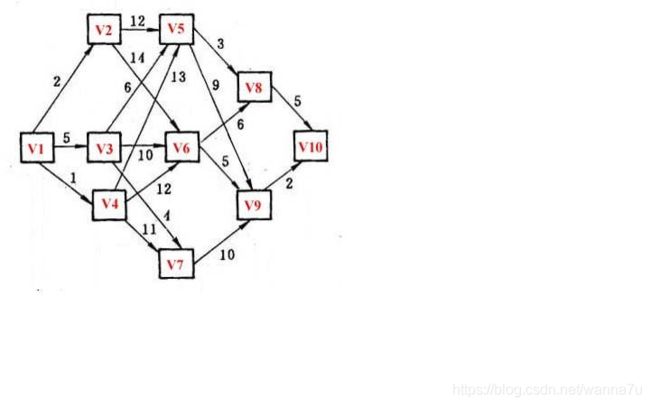
Sample Input

10
0 2 5 1 0 0 0 0 0 0
0 0 0 0 12 14 0 0 0 0
0 0 0 0 6 10 4 0 0 0
0 0 0 0 13 12 11 0 0 0
0 0 0 0 0 0 0 3 9 0
0 0 0 0 0 0 0 6 5 0
0 0 0 0 0 0 0 0 10 0
0 0 0 0 0 0 0 0 0 5
0 0 0 0 0 0 0 0 0 2
0 0 0 0 0 0 0 0 0 0

Sample Output

minlong=19
1 3 5 8 10

理解

	讲道理这题一上手我就满脑子的dfs，后来发现不用那么麻烦，就直接递归，从出口从后往前递推即可

AC代码

#include 
using namespace std;
int m[150][150] = {
     0},fee[105] = {
     0},lx[105] = {
     0};
int main(){
     
    int n;
    cin >> n;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= n;j++)
            cin >> m[i][j];
    for(int i = 1;i <= n;i++) fee[i] = 0x3f3f3f3f;
    fee[n] = lx[n] = 0;
    for(int i = n - 1;i >= 1;i--){
      //从出口从后往前递推 
        for(int j = i + 1;j <= n;j++){
     
            if(m[i][j] && m[i][j] + fee[j] < fee[i]){
     
                fee[i] = m[i][j] + fee[j];
                lx[i] = j;
            } 
        }
    }
    cout << "minlong=" << fee[1] << endl;
    int k = 1;
    cout << 1;
    while(k){
     
        if(k != 1) cout << " " << k;
        k = lx[k];
    }
     
    cout << endl; 
    return 0;
} 

G - 导弹拦截2

题目描述

    某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
    输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

Input

    输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000）

Output

    输出有2行。
    第1行是最多能拦截的导弹数，第2行是要拦截所有导弹最少要配备的系统数。

Sample Input

389 207 155 300 299 170 158 65

Sample Output

6
2

理解

因为之前的导弹拦截是用贪心写的，所以一拿到题就满脑子想着贪心可解的固定思维。
然后另一个要求输出最多能拦截的导弹数，这其实就是变相计算最长下降子序列

AC代码

#include 
using namespace std;
const int N = 100000 + 5;
int a[N],b[N],f[N],high[N];;
 
int main(){
     
    int n = 0; 
    while(cin >> a[++n]){
     }
    n--;
    int ans = 1;
    int t = 0;
    for(int i = 1;i <= n;i++){
     
        f[i] = 1;
        for(int j = t;j > 0;j--){
     
            if(a[b[j]] >= a[i]){
     
                f[i] = f[b[j]] + 1;
                break;
            }
        }
        t = max(t,f[i]);
        b[f[i]] = i;
        ans = max(ans,f[i]);
    }
    cout << ans << endl;
    for(int i = 1;i <= n;i++){
     
        high[i] = 30005; 
    }
    for(int i = 1;i <= n;i++){
     
        for(int j = 1;j <= i;j++){
     
            if(high[j] >= a[i]){
     
                high[j] = a[i];
                break;
            }
        }
    }
    int cnt = 0;
    for(int i = 1;i <= n;i++){
     
        if(high[i] != 30005){
     
//          cout << high[i] << endl;
            cnt++;
        }
    }
    cout << cnt << endl;
    return 0;
}

H - 合唱队形

题目描述

     N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学排成合唱队形。
     合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1, 2, …, K，他们的身高分别为T1, T2, …, TK，则他们的身高满足T1 < T2 < … < Ti , Ti > Ti+1 > … > TK (1≤i≤K)。
     你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

Input

     输入有多行，第一行是一个整数N（2 ≤ N ≤ 100），表示同学的总数。第二行有n个整数，用空格分隔，第i个整数Ti（130 ≤ Ti ≤ 230）是第i位同学的身高（厘米）。

Output

     输出只有一行，这一行只包含一个整数，就是最少需要几位同学出列。

Sample Input

8
186 186 150 200 160 130 197 220

Sample Output

4

理解

水题。只需双向判断最长升序子序列然后加一加减去中间重复量即可。

提示
对于50%的数据，保证有n ≤ 20；对于全部的数据，保证有n≤100。

AC代码

#include 
using namespace std;
const int N = 100 + 5;
int main(){
     
    int n,ans;
    cin >> n;
    int a[N]={
     0},sx[N]={
     0},jx[N]={
     0};
    for(int i = 1;i <= n;i++) cin >> a[i];
    a[0] = 0;
    for(int i = 1;i <= n;i++)
        for(int j = 0;j < i;j++)
            if(a[i] > a[j])
                sx[i] = max(sx[i],sx[j]+1);
    a[n+1] = 0;
    for(int i = n;i;i--)
        for(int j = n+1;j > i;j--)
            if(a[i] > a[j])
                jx[i] = max(jx[i],jx[j]+1);
    for(int i = 1;i <= n;i++) ans = max(ans,sx[i]+jx[i]-1);
    cout << n - ans << endl;
    return 0;
}

I - 开心的天宝

题目描述

    家里买的新房要交付了，天宝很开心，新房有属于自己的一个房间。更令她开心的是，妈妈说：“给你一些钱，你自己买一些东西吧，但是不能超过N元啊”。今天一早天宝就开始做规划了，他想买好多东西，但是会超过妈妈限定的预算。于是，她把每件物品规定了一 个重要度，分为5等：用整数1~5表示，第5等最重要。他还从因特网上查到了每件物品的价格（都是整数元）。她希望在不超过N元（可以等于N元）的前提 下，使每件物品的价格与重要度的乘积的总和最大。
设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为 j1，j2，……，jk，则所求的总和为：
    v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]w[jk]。 （其中为乘号）
    请你帮助天宝设计一个满足要求的购物单。

Input

    输入的第1行，为两个正整数，用一个空格隔开：
    N m（其中N（<30000）表示总钱 数，m（<25）为希望购买物品的个数。）
    从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有2个非负整数 v p（其中v表示该物品的价格(v<=10000)，p表示该物品的重要度(1~5)）

Output

    输出只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<100000000）。

Sample Input

1000 5
800 2
400 5
300 5
400 3
200 2

Sample Output

3900

理解

一个很神奇的让我RE的题目，本来就是照着背包模板老老实实存下来的来着，数组也开了很大放在了外面，然鹅就是RE。
大佬说预处理然后直接判断比你这样简单，于是，我改了...就很真实

AC代码

#include 
using namespace std;
int dp[30005];
int main(){
     
    int n,m;
    cin >> n >> m;
    int rec[30];
    memset(dp,0,sizeof(dp));
    for(int i = 0;i < m;i++){
     
        int money,vl;
        cin >> money >> vl;
        rec[i] = money * vl;
        for(int j = n;j >= money;j--){
     
            dp[j] = max(dp[j],dp[j-money]+rec[i]);
        }
    }
    cout << dp[n] << endl;
    return 0;
}

J - 逃亡总动员

题目描述

    在《Harry Potter and the Deathly Hallows》中，Harry Potter他们一起逃亡，现在有许多的东西要放到赫敏的包里面，但是包的大小有限，所以我们只能够在里面放入非常重要的物品，现在给出该种物品的数量、体积、价值的数值，希望你能够算出怎样能使背包的价值最大的组合方式，并且输出这个数值，赫敏会非常地感谢你。

Input

    第1行有2个整数，物品种数n和背包装载体积v。
第2行到n+1行每行3个整数，为第i种物品的数量m、体积w、价值s。

Output

    仅包含一个整数，即为能拿到的最大的物品价值总和。

Sample Input

2 10
3 4 3
2 2 5

Sample Output

13

理解

朴素的我的套模板写法TLE了（表示不服的小声bb）
然后紫妈告诉我，之前也有人tle了很久，他用的是位运算符

【注释】
选第一种一个，第二种两个。
结果为31+52=13
【数据规模】
对于30%的数据
1<=v<=500
1<=n<=2000
1<=m<=10
1<=w<=20
1<=s<=100
对于100%的数据
1<=v<=500
1<=n<=2000
1<=m<=5000
1<=w<=20
1<=s<=100

AC代码

#include 
using namespace std;
 
int main(){
     
    int n,v;
    cin >> n >> v;
    int m[n],w[n],s[n];
    for(int i = 0;i < n;i++){
     
        cin >> m[i] >> w[i] >> s[i];
    }
    int dp[5005]={
     0};
    for(int i = 0;i < n;i++){
     
        if(m[i] * w[i] >= v){
     
            for(int j = w[i];j <= v;j++) dp[j] = max(dp[j],dp[j - w[i]] + s[i]);
        }
        else{
     
            int k = 1;
            while(k <= m[i]){
     
                for(int j = v;j >= k*w[i];j--) dp[j] = max(dp[j],dp[j - k*w[i]] + k*s[i]);
                m[i] -= k;
                k <<= 1;
            }
            for(int j = v;j >= m[i]*w[i];j--) dp[j] = max(dp[j],dp[j - m[i]*w[i]] + m[i]*s[i]);
        }
    }
    cout << dp[v] << endl;
    return 0;
}

K - 科技庄园

题目描述

    Life是codevs的用户，他是一个道德极高的用户，他积极贯彻党的十八大精神，积极走可持续发展道路，在他的不屑努力下STN终于决定让他在一片闲杂地里种桃，以亲身实践种田的乐趣，厉行节约，告诉人们节约的重要性！
    春华秋实，在这个金秋的季节，Life带者他的宠物——PFT到了他的试验田，当他看见自己的辛勤成果时，心里是那个高兴啊！
    这时Life对他的宠物PFT说：“你想不想吃桃啊？”
    PFT兴奋的说：“好啊！”
    Life说：“好吧，但是我只给你一定的时间，你必须在规定的时间之内回到我面前，否则你摘的桃都要归我吃！”
    PFT思考了一会，最终答应了！
    由于PFT的数学不好！它并不知道怎样才能在规定的时间获得最大的价值，但你是一个好心人，如果你帮助它，你的RP一定会暴涨的！
    对于这个可以RP暴涨机会，你一定不会错过的是不是？
    由于PFT不是机器人，所以他的体力并不是无限的，他不想摘很多的桃以至体力为0，而白白把桃给Life。同时PFT每次只能摘一棵桃树，每棵桃树都可以摘K次（对于同一棵桃每次摘的桃数相同）。每次摘完后都要返回出发点（PFT一次拿不了很多）即Life的所在地（0，0）{试验田左上角的桃坐标是（1，1）}。
    PFT每秒只能移动一个单位，每移动一个单位耗费体力1(摘取不花费时间和体力,但只限上下左右移动)。

Input

    第1行：四个数为N，M，TI，A 分别表示试验田的长和宽，Life给PFT的时间，和PFT的体力。
    下面一个N行M列的矩阵桃田。表示每次每棵桃树上能摘的桃数。
    接下来N行M列的矩阵，表示每棵桃最多可以采摘的次数K。

Output

    一个数：PFT可以获得的最大的桃个数。

Sample Input

4 4 13 20
10 0 0 0
0 0 10 0
0 0 10 0
0 0 0 0
1 0 0 0
0 0 2 0
0 0 4 0
0 0 0 0

Sample Output

10

理解

【样例解释】
可以摘到1次（1，1）或1次（2，3）或1次（3，3），体力和时间不满足再摘桃了。
【数据范围】
对于M N TI A
10<=30%<=50
10<=100%<=100
对于K
10<=100%<=100
保证结果在longint范围内

AC代码

#include 
using namespace std;
int dp[20000];
int peach[1005][1005];
int cnt[1005][1005];
int w[500000],value[500000];
int main(){
       
    int n,m,tim,a;
    cin >> n >> m >> tim >> a;
    for(int i = 1;i <= n;i++){
     
        for(int j = 1;j <= m;j++){
     
            scanf("%d",&peach[i][j]);
        }
    }
    memset(dp,0,sizeof(dp));
    int ans = 1;
    for(int i = 1;i <= n;i++){
     
        for(int j = 1;j <= m;j++){
     
            scanf("%d",&cnt[i][j]);
            if(peach[i][j] > 0){
     
                for(int k = ans;k <= ans + cnt[i][j];k++){
     
                    w[k] = (i+j)*2; //往返疲劳双倍 
                    value[k] = peach[i][j];
                }
            }
            ans += cnt[i][j];
        }
    }
    a = min(a-1,tim);
    for(int i = 1;i <= ans;i++){
     
        for(int j = a;j >= w[i];j--){
     
            if(j-w[i] < 0) break;
            else dp[j] = max(dp[j],dp[j-w[i]]+value[i]);
        }
    }
    cout << dp[a] << endl;
    return 0;
}

（三）个人感受

本周感想

ccpc网络赛很自闭，海底捞很好吃（啊不是）…队友很强，签到签完了，然后钓了一年的鱼。果然学以致用中间需要反复地练习，不是学会了就能用得上的。背包这块感觉写题的时候一直在套模板来着…ummm而且有个题tle了，还是听了紫妈说的改位运算才A的，果然知识是相通的，之前总感觉落下了很多内容，希望能找到时间补，最近陷入了不知道忙啥但也写不完题目的怪圈，生活不易，猫猫叹气。有、累了，但路还很长，对吧。