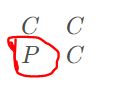题意分析
HDU - 6708
题意:给出一个整数k,要求你输出一个长和宽均为2^k^ 的符合要求的矩阵。比如k等于1时输出
\[ \begin{matrix} C & C \\ P & C \end{matrix} \]k = 2时输出
\[ \begin{matrix} C & C & C & C \\ P & C & P & C \\ P & P & C & C \\ C & P & P & C \end{matrix} \]
样例乍一看好像是第一个矩阵规定为k=1这种样子,后一个矩阵则以前一个矩阵为基础,可以将矩阵平分为四块(竖着切和横着切),每一部分正好对应前一个矩阵的整体,只有左下角那一块例外,对应的是前一块矩阵的”反面“(也就是C变为P,P变为C),不过这样仍然没有什么思路,后来观察发现上一块矩阵的某一个元素刚好对应下一个矩阵的某一块元素,比如对于字母C,有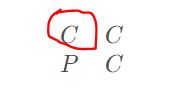
这样根据它们的相对位置,就不难给出所有情况的矩阵了。具体位置关系在代码中给出。
AC代码
关于代码,的确有些冗长,感觉应该有其他更简便方法表示这种规律,欢迎大佬评论指出。
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1024 + 10;
int T, k;
char s1[maxn][maxn], s2[maxn][maxn], s3[maxn][maxn], s4[maxn][maxn], s5[maxn][maxn], s6[maxn][maxn], s7[maxn][maxn], s8[maxn][maxn], s9[maxn][maxn], s10[maxn][maxn];
void init()
{
for(int i = 1; i <= 2; i++)
{
for(int j = 1; j <= 2; j++)
{
if(s1[i][j] == 'C')
{
//规律如下,此后的直接套用即可
for(int k = (j-1)*2+1; k <= (j-1)*2+2; k++)
s2[(i-1)*2+1][k] = 'C';
s2[(i-1)*2+2][(j-1)*2+1] = 'P', s2[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s2[(i-1)*2+1][k] = 'P';
s2[(i-1)*2+2][(j-1)*2+1] = 'C', s2[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 4; i++)
{
for(int j = 1; j <= 4; j++)
{
if(s2[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s3[(i-1)*2+1][k] = 'C';
s3[(i-1)*2+2][(j-1)*2+1] = 'P', s3[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s3[(i-1)*2+1][k] = 'P';
s3[(i-1)*2+2][(j-1)*2+1] = 'C', s3[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 8; i++)
{
for(int j = 1; j <= 8; j++)
{
if(s3[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s4[(i-1)*2+1][k] = 'C';
s4[(i-1)*2+2][(j-1)*2+1] = 'P', s4[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s4[(i-1)*2+1][k] = 'P';
s4[(i-1)*2+2][(j-1)*2+1] = 'C', s4[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 16; i++)
{
for(int j = 1; j <= 16; j++)
{
if(s4[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s5[(i-1)*2+1][k] = 'C';
s5[(i-1)*2+2][(j-1)*2+1] = 'P', s5[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s5[(i-1)*2+1][k] = 'P';
s5[(i-1)*2+2][(j-1)*2+1] = 'C', s5[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 32; i++)
{
for(int j = 1; j <= 32; j++)
{
if(s5[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s6[(i-1)*2+1][k] = 'C';
s6[(i-1)*2+2][(j-1)*2+1] = 'P', s6[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s6[(i-1)*2+1][k] = 'P';
s6[(i-1)*2+2][(j-1)*2+1] = 'C', s6[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 64; i++)
{
for(int j = 1; j <= 64; j++)
{
if(s6[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s7[(i-1)*2+1][k] = 'C';
s7[(i-1)*2+2][(j-1)*2+1] = 'P', s7[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s7[(i-1)*2+1][k] = 'P';
s7[(i-1)*2+2][(j-1)*2+1] = 'C', s7[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 128; i++)
{
for(int j = 1; j <= 128; j++)
{
if(s7[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s8[(i-1)*2+1][k] = 'C';
s8[(i-1)*2+2][(j-1)*2+1] = 'P', s8[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s8[(i-1)*2+1][k] = 'P';
s8[(i-1)*2+2][(j-1)*2+1] = 'C', s8[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 256; i++)
{
for(int j = 1; j <= 256; j++)
{
if(s8[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s9[(i-1)*2+1][k] = 'C';
s9[(i-1)*2+2][(j-1)*2+1] = 'P', s9[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s9[(i-1)*2+1][k] = 'P';
s9[(i-1)*2+2][(j-1)*2+1] = 'C', s9[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 512; i++)
{
for(int j = 1; j <= 512; j++)
{
if(s9[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s10[(i-1)*2+1][k] = 'C';
s10[(i-1)*2+2][(j-1)*2+1] = 'P', s10[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s10[(i-1)*2+1][k] = 'P';
s10[(i-1)*2+2][(j-1)*2+1] = 'C', s10[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
}
int main()
{
// freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
memset(s1, 'C', sizeof(s1));
cin >> T;
s1[2][1] = 'P';
init();
while(T--)
{
cin >> k;
for(int i = 1; i <= (int)(pow(2, k)); i++)
{
for(int j = 1; j <= (int)(pow(2, k)); j++)
{
if(k == 1)
cout << s1[i][j];
else if(k == 2)
cout << s2[i][j];
else if(k == 3)
cout << s3[i][j];
else if(k == 4)
cout << s4[i][j];
else if(k == 5)
cout << s5[i][j];
else if(k == 6)
cout << s6[i][j];
else if(k == 7)
cout << s7[i][j];
else if(k == 8)
cout << s8[i][j];
else if(k == 9)
cout << s9[i][j];
else if(k == 10)
cout << s10[i][j];
}
cout << endl;
}
}
}