并发数据结构Leapfrog Probing

Leapfrog Probing

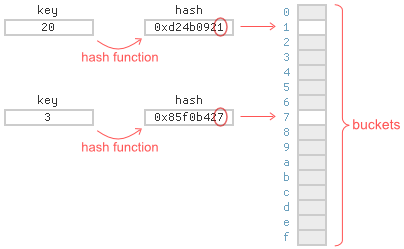
一个hash table是用来存取一系列key/value对，有很多方式用来实现一个hash table。但是都有一个共同点就是桶，每一个hash table都会包含一系列的桶，对于每一个key来说都会唯一的属于一个桶。为了决定某个key是属于哪个桶，你需要对这个key进行hash，然后对它取模，其余数就是这个key所属于的桶下标，整个过程如下图:

不可避免的，最终会有一系列 key会属于相同的桶，对于这种情况该如何处理呢？ 一个比较著名的策略就是把这些属于相同桶的key都存在一个单链表里面，这也就是所谓的拉链法，如下图:



拉链法对于现代CPU来说相对较慢，它需要很多指针的解析，并且对缓存也不友好(因为数据不连续，不能利用数据的局部性)，除了拉链法外，还有另外一个常用的策略，开放地址法，这种方法把所有的 key都放在桶中，这种方法对缓存比较友好，如果没有找到空闲的桶存放这个key，则会利用一些策略去寻找附近的空闲的桶，而这种方法的缺点就是当这个桶满的时候，你可能查询一个key需要搜索很多桶，这取决于你的探测策略。

线性探测

线性探测是最为简单的一种探测策略，加入我们插入(13,"orange")，到hash table中，通过hash计算出13的hash值是0x95bb7b92，那么我们将会按照其最低位把它存在索引是2的桶中的，但发现对应的桶中已经有元素了，那么此时在2的基础上累加，继续看索引3，以此类推。最终找到一个空闲的位置把(13,"orange")插入进去，整个过程如下图:

可见线性探测的效率并不高，每次插入都需要遍历大部分的已经有元素的桶，会有 聚集现象。

二次探测

二次探测较线性探测效率高，线性探测在发生冲突的时候，每次递增1，而二次探测则是按照下面这个公式来探测。

H0 = hash(x) % m;
Hi = (H0 + i^2) % m
Hi = (H0 - i^2) % m 
其中i = 1,2,....(m-1)/2

第一次都一样，取hash，然后按照桶的个数取余数即可，第二次在第一次的基础上加i^2(此时i=1)，第三次的时候，在第一次的基础上减i^2(此时i=2)，以此类推。二次探测相比于线性探测来说可以避免聚集(属于相同桶的key顺序排列在一起)现象。然而二次探测又引入了另外一种聚集问题,就是所有映射到相同桶的关键字在寻找空位的时候的探测步长都是固定的。为了解决这个二次聚集的问题引入了重hash。

重hash

二次聚集产生的原因是二次探测算法产生的探测序列步长总是固定的，如1, 4, 9, 16等，现在需要的一种方法是产生一种依赖关键字的探测序列，而不是每个关键字都一样，那么，即使不同的关键字映射到了相同的桶，也可以使用不同的探测序列。方法就是把不同的关键字用不同的哈希函数再做一遍哈希化，用这个结果作为步长，对指定的关键字步长在整个探测中的不变的，不同的关键字使用不同的步长。 第二个哈希函数应具备的要点：1.和第一个哈希函数不同；2.不能输出0（否则，将没有步长；每次探测都是原位置，算法将陷入死循环）

布谷鸟hash(Cuckoo hashing)

Cuckoo_hashing，关于Cuckoo Hash可以参考wiki上的介绍，这种探测策略具有占用空间小查询迅速等特性，可以用于Bloom filter，内存管理等。它的原理也很简单，类似于布谷鸟在别的鸟巢中下蛋，并将别的鸟蛋挤出的行为。算法使用两个不同哈希函数计算对应key所属于的桶。

1. 当两个哈希得到的两个桶都为空，则任意选择一个桶插入即可
2. 让两个哈希得到的两个桶有一个为空，则插入到空桶中
3. 当两个哈希得到的两个桶均不为空，则随机选择两者之一的位置上key 踢出，计算踢出的key的另一个哈希值对应的位置进行插入，转至2执行（即当再次插入位置为空时插入，仍旧不为空时，再踢出这个key）

布谷鸟hash还有很多变形，其中一种就是通过增加hash函数，进一步提高空间的利用率，还有一种则是增加哈希表，每个哈希函数对应一个哈希表，每次选择多个张表中空余桶进行放置。

跳房子Hash(Hopscotch hashing)

Hopscotch hashing，非常适合去实现一个并发的HashMap。

首先对key进行hash得到桶的下标i。

1. 如果下标为i的桶是空的，则插入key到桶中，然后返回。
2. 如果不为空，则从i开始线性探测，直到找到一个空闲的桶，下标为j
3. 如果j距离i在H-1范围内，则把key插入到桶中然后返回，否则认为j远离了i，为了找到一个离i近的，空闲的桶，需要找到一个桶在i和j之间并且距离j在H-1范围内，然后把j替换成y，这个时候y所在的位置就空闲起来了，这个时候再查看y是否距离i在H-1范围内，如果不在就继续步骤3直到找到一个符号条件的就把key插入到桶中，如果最终没有找到就进行hash table扩容。

Leapfrog Probing

这是作者Jeff Preshing发明的一个解决hash冲突的方法灵感来自于Hopscotch hashing，也是本文重点要介绍的一种算法。在Leapfrog Probing算法中，我们需要给每个桶配置两个额外的空间，这个空间里面存的值就决定了每个桶的探测策略，如下图:

为了查找指定的key所在桶，查找过程如下:

1. 计算key的hash值，然后取模得到对应的桶下标，然后去检查这个桶是否为空
2. 如果这个桶不为空，就使用这个桶对应的第一个空间中的值，作为步长加上当前桶所在索引，得到新的桶下标。
3. 如果新下标的桶仍不为空，则使用这个桶对应的第二个空间中的值作为步长，再次计算桶的下标，此后探测的步长都取自第二个空间中的值，直到为0

例如: 插入40到hash table中，通过hash计算得到其值为0x674a0243，通过取模得到对应的桶是3，因此首先检查下标为3的如果不为空，则取第一个空间中的值2作为步长，再次检查下标为5的桶，依然不为空，取第二个空间中的值3，再次检查下标为8的桶，此时桶为空，查找到此结束。 整个查找过程严重依赖空间中的值，那么如何得到这些值变得很关键，而这整个过程都是在插入的时候完成。插入一个元素到hash table中要分为两步，如果key要插入的桶已经满了，并且第一个空间中的值不为0，这个时候需要使用Leapfrog Probing进行探测，否则的话走线性探测，找到一个空闲的桶，并把下标写到初始桶的第一个空间中，例如插入一个key为orange，通过hash计算得到0x95bb7d92，根据取模得到桶下标为2，但是下标为2的桶已经满了，并且第一个空间中的值是0，然后走线性探测，找到下标为11的桶是空闲的，则把key插入，并把下标为2的桶的第一个空间中的值设置为9。那么下次查找的时候直接通过第一个空间中的值就可以很快查找到了。整个过程如下图:

最后我们来谈一下针对 Leapfrog Probing的并发处理，第一种是 insert和 get的并发，对于 insert来说，要分成两步，第一步是把key存放到桶中，第二步是更新空间中的值。这两步都可以实现为原子操作，但是两者组合在一起并不是原子的，当把key存放到桶中的时候，还没有更新空间中的值此时如果有对相同key的查询请求是无法查询到的，直接返回 NullValue，以此来处理 insert和 get的并发，针对多 insert的并发处理则需要更多关注。这种情况很复杂，如果有两个key属于同一个桶并发插入的时候，当第一个key开始做线性探测寻找空闲的桶，然后更新空间中的值的时候，对于第二个key来说是不可见的，如果这个时候第二个key同事也进行探测，然后找到一个空闲的桶，随机更新空间的值，这将会导致两个key不一致，因此简单来做的话就是第二key自旋等待第一个key插入的结果可见。

参考文献

• Leapfrog Probing

本文是对文章 Leapfrog Probing的学习总结。