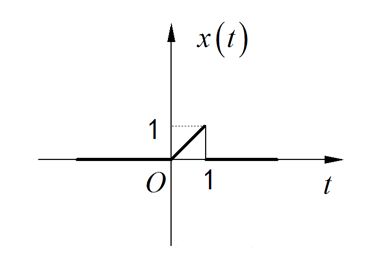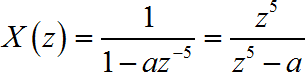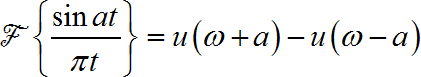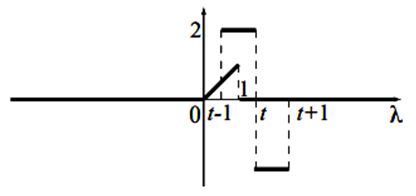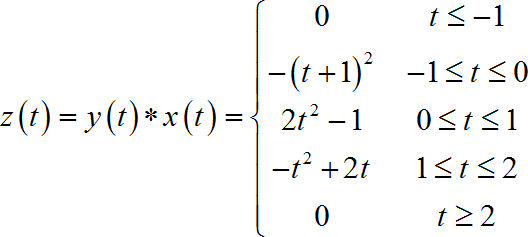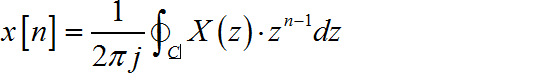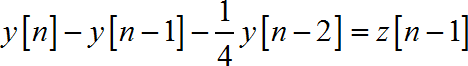信号与系统2020参考答案(网络试卷)
00特殊情况说明
在2020年春季学期,由于受到Coronavirus-19的影响,考试采用网络考试的形式:
- 通过网络学堂分发试卷和收集答案;
- 考试通过腾讯会议进行监考过程;
- 考试时间6月13日下午2:30-4:45
在试卷的第一页有“考试诚信承诺书”需要参试学生必须誊写在答题纸上的第一页。
▲ 网络考试诚信承诺书试卷布置情况
01不定项选择题答案表格
一、不定项选择题:(10×1=10分,将答案写在试卷前面的答案表格1中)
- 下面信号中,那些是能量有限信号?
2、下面信号中,那些是周期信号?
- 下面系统中,属于时不变系统的包括哪些?其中 x ( t ) , x ( t ) x\left( t \right),x\left( t \right) x(t),x(t)为系统的输入, y ( t ) , y [ n ] y\left( t \right),y\left[ n \right] y(t),y[n]为系统的输出。
4、下面各图中LTI系统函数的零极点分布,所描述的幅频特性为带阻系统为:

5、已知LTI系统在 x ( t ) x\left( t \right) x(t)作用下系统零状态输出为 y ( t ) y\left( t \right) y(t) 。那么在 x 1 ( t ) x_1 \left( t \right) x1(t) 作用下,系统的零状态输出为:

6、已知实信号 x ( t ) , y ( t ) x\left( t \right),y\left( t \right) x(t),y(t)之间的关系为

下面关于信号 y ( t ) y\left( t \right) y(t) 的频谱 Y ( ω ) Y\left( \omega \right) Y(ω)叙述正确的是:

7、下面半边周期冲激序列的拉普拉斯变换为:

8、可能与下面s平面区域对应的z平面区域为( ):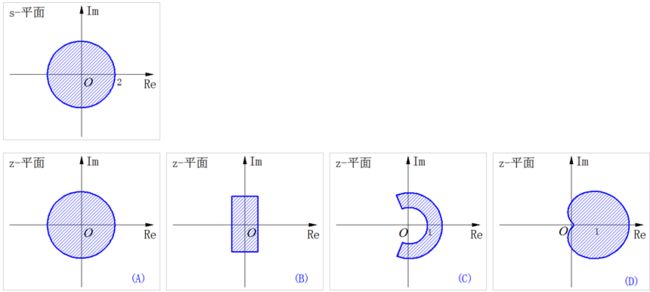
9、如果模拟信号在采样频率 ω s \omega _s ωs 下进行采样,转换成数字信号。那么其中模拟频率为 ω s 3 { {\omega _s } \over 3} 3ωs的信号在采样后对应的数字信号频率(归一化频率)为:

10、下面周期信号中的频率成分包括有:
02判断对错题答案表格
![]()
1、如果 x ( t ) x\left( t \right) x(t) 的Nyquist频率为 ω N \omega _N ωN ,那么 x 2 ( t ) x^2 \left( t \right) x2(t) 的Nyquist频率为 2 ⋅ ω N 2 \cdot \omega _N 2⋅ωN。
2、不存在信号本身与它的频谱都是有限长的信号。
3、有限冲激响应(FIR)滤波器的传递函数的分母是常量。
4、如果一个线性时不变离散时间系统的系统函数的收敛域包含单位圆,则系统是BIBO稳定的。
5、如果稳定最大相位的LTI系统函数具有靠近虚轴的零点,那么在零点对应虚轴所在的频率附近,系统的幅频特性有一个低谷,相位呈现下降趋势。
03填空题
1、已知两个序列 u [ n ] , v [ n ] u\left[ n \right],v\left[ n \right] u[n],v[n]的波形如下图所示,请写出它两的卷积 w [ n ] = u [ n ] ∗ v [ n ] w\left[ n \right] = u\left[ n \right] * v\left[ n \right] w[n]=u[n]∗v[n] 在 n = 2 n = 2 n=2时的取值: w [ 2 ] = 1 w\left[ 2 \right] = \,\,\,1 w[2]=1.
2、一个线性时不变系统的输入输出分别 x ( t ) , y ( t ) x\left( t \right),y\left( t \right) x(t),y(t) ,它们之间的关系可以由下面的微分方程所描述:
其中 w ( t ) w\left( t \right) w(t)是中间变量。
那么该系统的系统函数为________。

系统的单位冲激响应 h ( t ) = − sin ( t ) ⋅ u ( t ) h\left( t \right) = - \sin \left( t \right) \cdot u\left( t \right) h(t)=−sin(t)⋅u(t)。
3、知信号 x ( t ) x\left( t \right) x(t) 的波形如下图所示,则该信号的拉普拉斯变换的表达式和响应的收敛域为:
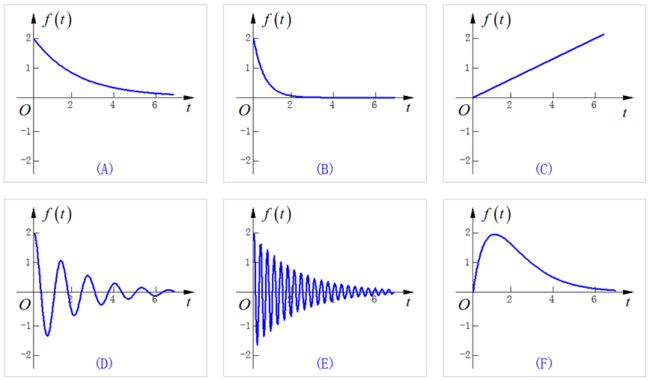
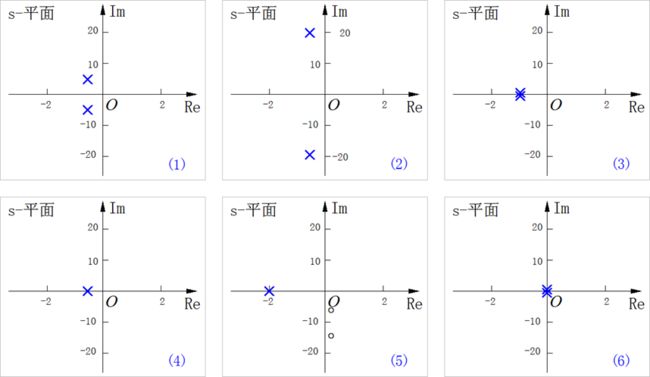
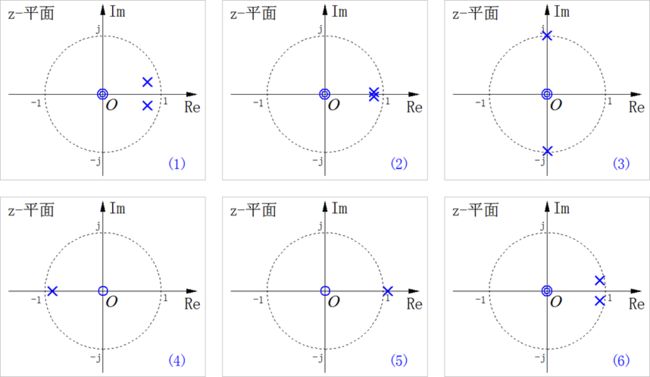
4、已知连续时间LTI系统的单位冲激响应信号波形如下图(A)(F)所示,在下图后面给出了六种零极点分布示意图(1)(6),请按照(A)~(F)对应单位冲激响应波形写出对应系统零极点分布顺序:(4),(5),(6),(1),(2),(3)。
5、已知离散时间LTI系统的零极点分布如下面(1)(6)图所示意。在下图后面又给出了六种单位冲激响应序列波形图(A)(F)。请写出(1)~(6)种零极点分布所对应的系统单位冲激响应序列的顺序:(D),(E),(F),(A),(B),(C)。
6、 已知离散时间序列 x [ n ] x\left[ n \right] x[n] 的表达式为: x [ n ] = ∑ k = 0 ∞ a k δ [ n − 5 k ] x\left[ n \right] = \sum\limits_{k = 0}^\infty {a^k \delta \left[ {n - 5k} \right]} x[n]=k=0∑∞akδ[n−5k] ,对应序列的图像为:

7、如果正弦波 x a ( t ) = cos ( 50 t ) x_a \left( t \right) = \cos \left( {50t} \right) xa(t)=cos(50t) 被采样,采样频率为 ω s = 30 r a d / s \omega _s = 30\,rad/s ωs=30rad/s。采样后的数据再经过DAC(数模转换)被转换成模拟信号。DAC的转换速率也是 30 rad/s。那么转换后重构的正弦信号的频率为: 10 rad/s 。
8、已知信号 x ( t ) x\left( t \right) x(t) 的拉普拉斯变换为:
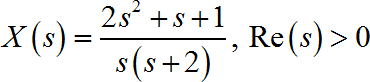
则信号的初值 x ( 0 + ) = − 3 x\left( {0_ + } \right) = - 3 x(0+)=−3,信号的终值 : x ( + ∞ ) = 0.5 x\left( { + \infty } \right) = 0.5 x(+∞)=0.5。
04简答题
1、请解释什么叫做"吉布斯现象",举例说明与"吉布斯现象"相关的物理现象。
"吉布斯现象"的一种解释:使用周期信号的有限项频谱合成的信号,如果原来的周期信号有间断点,合成信号在间断点出有过冲。过冲幅值大约是信号间断点跳跃幅值的9%左右。随着合成项数增加,过冲幅值维持在9%左右

举例:可以结合在现实生活中对应的有限带通系统在观察信号所出现的“振铃”现象进行说明,或者通过物理中的傅里叶光学现象来阐述光的衍射现象等。
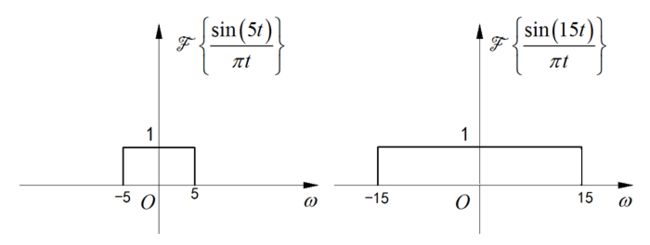
2、请解释什么叫做"频率泄露",并说明如何减少频率泄露现象对信号分析的影响。
对信号进行截取,截取后的信号频谱会出现"频率泄露"现象。信号频谱的高频段和低频段都会出现波动,并会出现过渡带。
下图显示了截取的sinc函数所对应的频谱出现的"频率泄露"现象。

回答体重需要包括产生“频率泄露”的原因来自于对信号的截取;“频率泄露”的现象反映在频谱的波动以及有过渡带等方面。
在减少频谱泄露对信号分析的影响方面需要包括有:扩大采集信号的时间窗口长度、使用光滑窗口对数据进行平滑等。
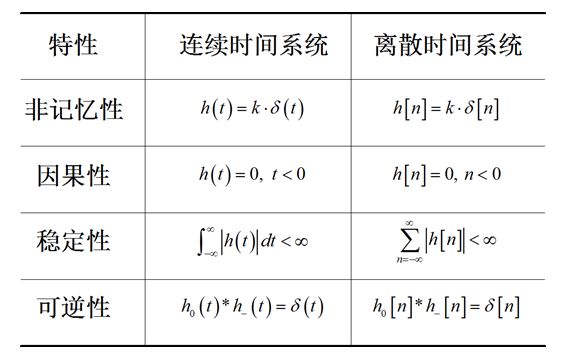
3、如果已知线性时不变系统的单位冲激相应信号 ,请说明如何判断系统的因果性、稳定性、可逆性、即时或者动态性。
通过语言或者公式对于LTI系统的单位冲激响应与系统的因果、稳定、可逆、即时动态等特性进行论述。
05计算题
1.小题1
已知信号 x ( t ) x\left( t \right) x(t)的表达式为:
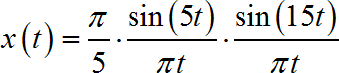
求信号的面积 A = ∫ − ∞ ∞ x ( t ) d t = ? A = \int_{ - \infty }^\infty {x\left( t \right)dt} = ? A=∫−∞∞x(t)dt=?
求解:
假设 X ( ω ) = F { x ( t ) } X\left( \omega \right) = F\left\{ {x\left( t \right)} \right\} X(ω)=F{ x(t)},有傅里叶的定义可以知道信号 x ( t ) x\left( t \right) x(t)的面积为:
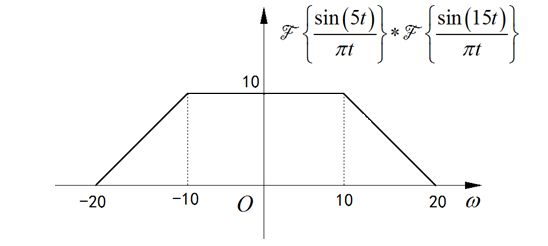
所以: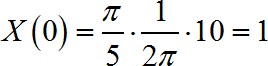
信号的面积为: ∫ − ∞ ∞ x ( t ) d t = 1 \int_{ - \infty }^\infty {x\left( t \right)dt} = 1 ∫−∞∞x(t)dt=1。
2.小题2
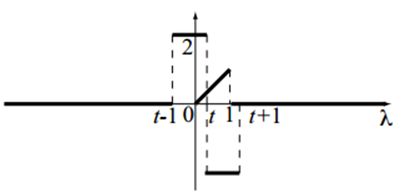
已知连续时间信号 x ( t ) , y ( t ) x\left( t \right),y\left( t \right) x(t),y(t) 如下图所示,请写出它们的卷积结果 z ( t ) = x ( t ) ∗ y ( t ) z\left( t \right) = x\left( t \right) * y\left( t \right) z(t)=x(t)∗y(t) 的表达式,并绘制出结果的信号波形。

求解:
根据卷积定义,首先将两个信号的变量由 t t t修改成 λ \lambda λ。然后在选择其中一个信号进行反转平移。在这里选择 x ( λ ) x\left( \lambda \right) x(λ) 进行反转:
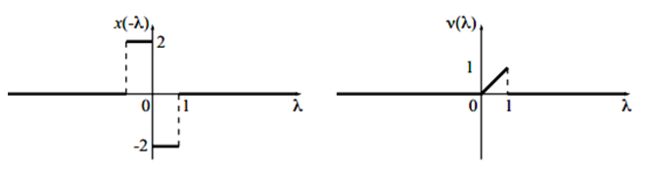
然后平移 x ( − λ ) x\left( { - \lambda } \right) x(−λ),形成 x ( t − λ ) x\left( {t - \lambda } \right) x(t−λ)。
(1)当 t ≤ − 1 t \le - 1 t≤−1或者 t ≥ 2 t \ge 2 t≥2的时候, x ( t − λ ) , y ( λ ) x\left( {t - \lambda } \right),y\left( \lambda \right) x(t−λ),y(λ)没有交集,卷积结果 z ( t ) = 0 z\left( t \right) = 0 z(t)=0。
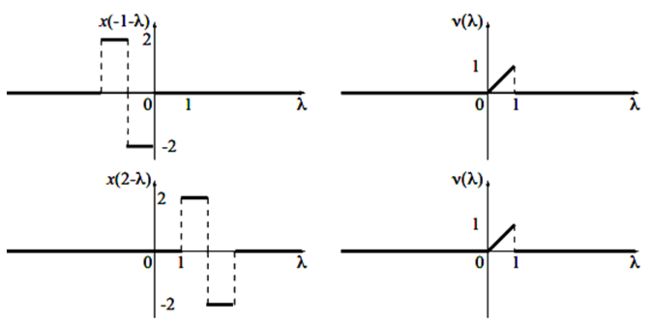
(2)当 − 1 ≤ t ≤ 0 - 1 \le t \le 0 −1≤t≤0时:
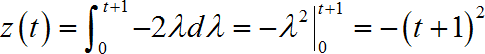
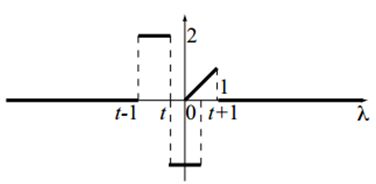
(3)当 0 ≤ t < 1 0 \le t{\kern 1pt} < 1 0≤t<1时:
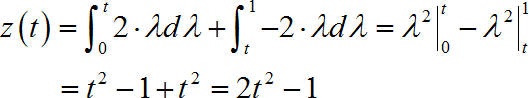
(4)当 1 ≤ t ≤ 2 1 \le t \le 2 1≤t≤2 时:
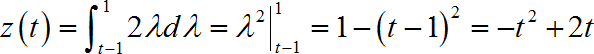
最后,将所有的结果写在一起:
3.小题3
收敛域为 1 < ∣ z ∣ < 2 1 < \left| z \right| < 2 1<∣z∣<2,求出原序列。
求解:
对 X ( z ) X\left( z \right) X(z)进行因式分解:

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST1.PY -- by Dr. ZhuoQing 2020-06-18
#
# Note:
#============================================================
from headm import *
from sympy import abc,apart,print_latex
z=abc.z
numerator=2*z**3-5*z**2+z+3
denominator = (z-2)*(z-1)
print_latex(apart(numerator/denominator/z))
tspexecutepythoncmd('msg2latex')
#------------------------------------------------------------
# END OF FILE : TEST1.PY
#============================================================
根据收敛域 1 < ∣ z ∣ < 2 1 < \left| z \right| < 2 1<∣z∣<2可以知道 x [ n ] x\left[ n \right] x[n]为:
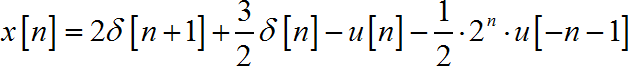
解法二:
因此 x [ n ] x\left[ n \right] x[n]就是求 X ( z ) ⋅ z n − 1 X\left( z \right) \cdot z^{n - 1} X(z)⋅zn−1的留数。根据n取值不同,下式
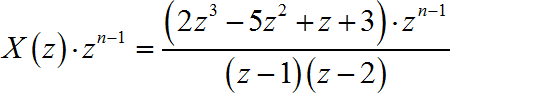
的具有不同的围线内的极点分布:
当 n ≥ 1 n \ge 1 n≥1时,上式具有 z = 1 z = 1 z=1处的极点,所以:
![]()
当 n = 0 n = 0 n=0时, z = 0 z = 0 z=0, z = 1 z = 1 z=1是围线积分中的两个极点:
R e s [ X ( z ) ⋅ z n − 1 ] z = 0 = 2 z 3 − 5 z 2 + z + 3 ( z − 1 ) ( z − 2 ) ∣ z = 2 = 1.5 {\mathop{\rm Re}\nolimits} s\left[ {X\left( z \right) \cdot z^{n - 1} } \right]_{z = 0} = \left. { { {2z^3 - 5z^2 + z + 3} \over {\left( {z - 1} \right)\left( {z - 2} \right)}}} \right|_{z = 2} = 1.5 Res[X(z)⋅zn−1]z=0=(z−1)(z−2)2z3−5z2+z+3∣∣∣∣z=2=1.5 R e s [ X ( z ) ⋅ z n − 1 ] z = 1 = − 1 {\mathop{\rm Re}\nolimits} s\left[ {X\left( z \right) \cdot z^{n - 1} } \right]_{z = 1} = - 1 Res[X(z)⋅zn−1]z=1=−1
所以: x [ 0 ] = 0.5 x\left[ 0 \right] = 0.5 x[0]=0.5。
当 n < 0 n < 0 n<0,根据留数第二定理,通过计算围线之外极点的留数,取负之后获得积分数值:
x [ n ] = R e s [ X ( z ) ⋅ z n − 1 ] z = 2 = − 2 n − 1 u [ − n − 1 ] x\left[ n \right] = {\mathop{\rm Re}\nolimits} s\left[ {X\left( z \right) \cdot z^{n - 1} } \right]_{z = 2} = - 2^{n - 1} u\left[ { - n - 1} \right] x[n]=Res[X(z)⋅zn−1]z=2=−2n−1u[−n−1]
综上所示:
4.第四小题
已知离散时间线性时不变系统的频率特性为: H ( e j Ω ) = j . tan ( Ω ) H\left( {e^{j\Omega } } \right) = j.\tan \left( \Omega \right) H(ejΩ)=j.tan(Ω) 。
请写出该离散时间统对应的差分方程。
求解:
根据:

所以:

将其中 e j Ω e^{j\Omega } ejΩ替换成z,可以得到系统的传递函数:

所以离散时间系统对应的差分方程为:
![]()
06计算卷积
已知序列 x [ n ] = [ 1 , 2 , 3 , 4 , 5 ] , h [ n ] = [ 1 , 0 , 1 , 1 ] x\left[ n \right] = [1,2,3,4,5],\,\,h\left[ n \right] = \left[ {1,0,1,1} \right] x[n]=[1,2,3,4,5],h[n]=[1,0,1,1]。
求:
(1) y [ n ] = x [ n ] ∗ h [ n ] y\left[ n \right] = x\left[ n \right] * h\left[ n \right] y[n]=x[n]∗h[n]
(2) y [ n ] = x [ n ] ⊗ 7 h [ n ] y\left[ n \right] = x\left[ n \right] \otimes _7 h\left[ n \right] y[n]=x[n]⊗7h[n]
(3) y [ n ] = x [ n ] ⊗ 8 h [ n ] y\left[ n \right] = x\left[ n \right] \otimes _8 h\left[ n \right] y[n]=x[n]⊗8h[n]
说明:序列 x [ n ] , h [ n ] x\left[ n \right],h\left[ n \right] x[n],h[n]中第一个数字对应下标 n = 0 n = 0 n=0。
运算符号 ⊗ 7 , ⊗ 8 \otimes _7 , \otimes _8 ⊗7,⊗8分别表示周期为7和8 的圆卷积。
求解:
(1) x [ n ] ∗ h [ n ] = [ 1 , 2 , 4 , 7 , 10 , 7 , 9 , 5 ] x\left[ n \right] * h\left[ n \right] = \left[ {1,2,4,7,10,7,9,5} \right] x[n]∗h[n]=[1,2,4,7,10,7,9,5]
(2) x [ n ] ⊗ 7 h [ n ] = [ 6 , 2 , 4 , 7 , 10 , 7 , 9 ] x\left[ n \right] \otimes _7 h\left[ n \right] = \left[ {6,2,4,7,10,7,9} \right] x[n]⊗7h[n]=[6,2,4,7,10,7,9]
(3) x [ n ] ⊗ 8 h [ n ] = [ 1 , 2 , 4 , 7 , 10 , 7 , 9 , 5 ] x\left[ n \right] \otimes _8 h\left[ n \right] = \left[ {1,2,4,7,10,7,9,5} \right] x[n]⊗8h[n]=[1,2,4,7,10,7,9,5]
07系统分析题
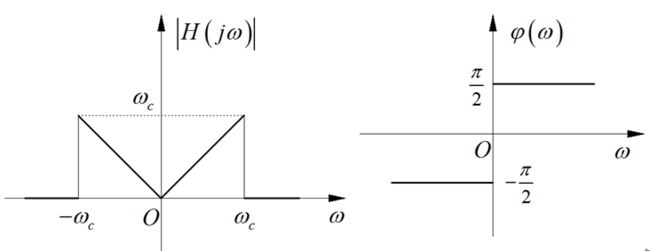
试画出 ∣ H ( j ω ) ∣ \left| {H\left( {j\omega } \right)} \right| ∣H(jω)∣ 和 ϕ ( ω ) \phi \left( \omega \right) ϕ(ω) 的图形。
求解:
08系统分析题
已知离散时间系统的系统框图如下图所示。其中子系统W的输入输出的关系为:
系统框图中的 z − 1 z^{ - 1} z−1 表示单位延迟
- 请写出系统的传递函数 H ( z ) H\left( z \right) H(z) ;
- 列写出输入 x [ n ] x\left[ n \right] x[n] 输出 y [ n ] y\left[ n \right] y[n]之间的差分方程;
- 根据系统的零极点分布,绘制出系统的幅频特性,判断幅频特性的种类(低通、带通、高通、带阻)。
求解:
1、 根据子系统W的输入输出差分方程,可以得到W系统的传递函数:

根据系统框图可以知道:

那么:

2、 根据 H ( z ) H\left( z \right) H(z)可以得到输入输出 x [ n ] , y [ n ] x\left[ n \right],y\left[ n \right] x[n],y[n] 之间的差分方程为:
以上两种形式的差分方程都是允许的。
3、 根据系统函数 的分子、分母的根,可以知道对应的零、极点分别是:

系统对应的幅频特性如下图所示。幅频特性属于带通滤波器。