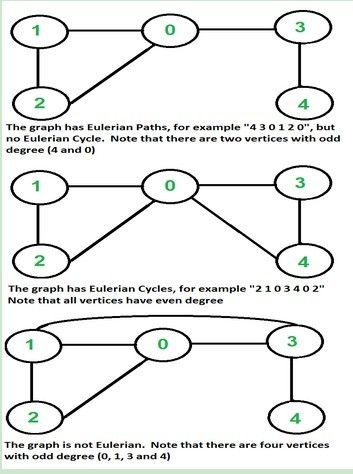
判断图中是否包含欧拉路径或者欧拉环

欧拉路径的定义：对于无向图来说，欧拉路径就是通过每条边有且只有一次，如果遍历的起始点和终止点都是一个顶点的话，那么就说这个图存在欧拉环。

上图中有三个例子，分别是欧拉路径和欧拉环，以及非欧拉路径。那么怎么来判断一个图中是否含有欧拉路径或者欧拉环呢。首先回想一下图的定义，图中有v个顶点，那么着v个顶点中有0个或者两个或者两个以上的顶点度数为奇数。接下来，求欧拉路径就相当于用笔画一个图，笔可以经过每一个顶点，画出某一条边有且只有一次，而不用离开纸张的表面。

如果一个图中含有一条欧拉路径，那么它就被称为半欧拉的。先看看第一幅图，含有欧拉路径图的特点，除了顶点0和顶点4之外，其他的顶点的度数都是偶数，这这个图中是2.

看第二幅图，所有的顶点的度数都是偶数，之后第三幅图，有4个顶点的度数是奇数。那么就能得到非欧拉路径和欧拉路径的区别就是非欧拉路径有超过2个以上的顶点度数为奇数。

给定欧拉环的算法：

1，对于所有度数不为0的顶点和他们之间的边组成的图进行检验，看看是否他们组成的图是连通的，如果所有顶点的度数都为0，那么我们可以说这个图是含有欧拉路径的。

2，判断所有的顶点的度数是否为偶数。

欧拉路径算法：

1，对于所有度数不为0的顶点和他们之间的边组成的图进行检验，判断他们组成的图是否是连通的。

2，对于所有第一步检验的顶点，判断他们之中有奇数度数的个数，如果超过2个以上度数为奇数，那么此图不含欧拉路径。

下面是代码：

#include
#include
using namespace std;

class Graph {
	int vexNum;
	list* adjacents;
public:
	Graph(int _vexNum);
	~Graph();
	void addEdge(int v, int w);
	void DFSUtil(int v, bool* visited);
	bool isConnected();
	int isEulerian();
};

Graph::Graph(int _vexNum) {
	vexNum = _vexNum;
	adjacents = new list[vexNum];
}

Graph::~Graph() {
	delete []adjacents;
}

void Graph::addEdge(int v, int w) {
	adjacents[v].push_back(w);
	adjacents[w].push_back(v);
}

void Graph::DFSUtil(int v, bool *visited) {
	visited[v] = true;
	list::iterator iter;
	for (iter = adjacents[v].begin(); iter != adjacents[v].end(); iter++)
		if (false == visited[*iter])
			DFSUtil(*iter, visited);
}

bool Graph::isConnected() {
	int v;
	bool* visited = new bool[vexNum];
	for (v = 0; v < vexNum; v++)
		visited[v] = false;
	for (v = 0; v < vexNum; v++)
		if (0 != adjacents[v].size())
			break;
	if (v >= vexNum)
		return true;
	DFSUtil(v, visited);
	for (v = 0; v < vexNum; v++)
		if (false == visited[v] && adjacents[v].size() > 0)
			return false;
	return true;
} 

int Graph::isEulerian() {// 0 represents non eulerian, 1 represents eulerian path, 2 represents eulerian cycle
	bool rst = isConnected();
	if (!rst)
		return 0;
	int v;
	int odd = 0;
	for (v = 0; v < vexNum; v++)
		if (adjacents[v].size() & 0x01)
			odd++;
	if (odd > 2)
		return 0;
	return odd ? 1 : 2;
}

void test(Graph& g) {
	int rst = g.isEulerian();
	if (0 == rst)
		cout << "there is no eulerian path or cycle" << endl;
	else if (1 == rst)
		cout << "there is a eulerian path" << endl;
	else
		cout << "there is a eulerian cycle" << endl;
}

int main(int argc, char* argv[]) {
	Graph g1(5);
    g1.addEdge(1, 0);
    g1.addEdge(0, 2);
    g1.addEdge(2, 1);
    g1.addEdge(0, 3);
    g1.addEdge(3, 4);
    test(g1);
 
    Graph g2(5);
    g2.addEdge(1, 0);
    g2.addEdge(0, 2);
    g2.addEdge(2, 1);
    g2.addEdge(0, 3);
    g2.addEdge(3, 4);
    g2.addEdge(4, 0);
    test(g2);
 
    Graph g3(5);
    g3.addEdge(1, 0);
    g3.addEdge(0, 2);
    g3.addEdge(2, 1);
    g3.addEdge(0, 3);
    g3.addEdge(3, 4);
    g3.addEdge(1, 3);
    test(g3);
 
    // Let us create a graph with 3 vertices
    // connected in the form of cycle
    Graph g4(3);
    g4.addEdge(0, 1);
    g4.addEdge(1, 2);
    g4.addEdge(2, 0);
    test(g4);
 
    // Let us create a graph with all veritces
    // with zero degree
    Graph g5(3);
    test(g5);
	cin.get();
	return 0;
}