【C语言->数据结构与算法】->哈夫曼压缩&解压缩->第一阶段->哈夫曼编码&解码的实现
文章目录
-
- Ⅰ 前言
- Ⅱ 代码实现哈夫曼编码&解码
-
- A. 构造哈夫曼树
-
- a. 频度统计
- b. 生成哈夫曼树
-
- ① 初始化节点
- ② 查找频度最小节点
- ③ 哈夫曼树的构造
- B. 哈夫曼编码
-
- a. 得到每个字符的编码
- b. 编码
- C. 解码
- Ⅲ 完整代码&运行结果
- Ⅳ 一条重要的小补充
Ⅰ 前言
在之前的文章里,我讲解了如何将一个字符串逐步生成哈夫曼树最后完成其编码,光说概念对编程是没有任何帮助的,这篇文章会用代码实现哈夫曼编码的构造过程。
这是完成最终项目——哈夫曼压缩&解压缩的第一部分,完成了这个阶段,后面只是改成文件级别的操作就可以了,代码的改动不会太大。
Ⅱ 代码实现哈夫曼编码&解码
按照之前我们讲哈夫曼树的时候,逐步做的一样,我们就按这个顺序来实现代码。

A. 构造哈夫曼树
首先我先给大家看一下这个代码需要的头文件,这是我自己的头文件tyz.h,里面是这个代码需要用到的宏和定义。
#ifndef _TYZ_H_
#define _TYZ_H_
#define TRUE 1
#define FALSE 0
#define NOT_FOUND -1
#define SET(value, index) (value |= 1 << (index ^ 7))
#define CLEAR(value, index) (value &= ~(1 << (index ^ 7)))
#define GET(value, index) ((value) & (1 << (index ^ 7)) != 0)
typedef unsigned char boolean;
typedef unsigned int u32;
typedef unsigned short u16;
typedef boolean u8;
int skipBlank(const char *str);
boolean isRealStart(int ch);
#endif
代码里的int我都用u32替代,其他类型也是一样,我都用位数来替代。因为哈夫曼压缩解压缩需要牵扯到将数据压缩成以位为单位的空间中,所以用位数来替代本身的名字更加方便一些。
a. 频度统计
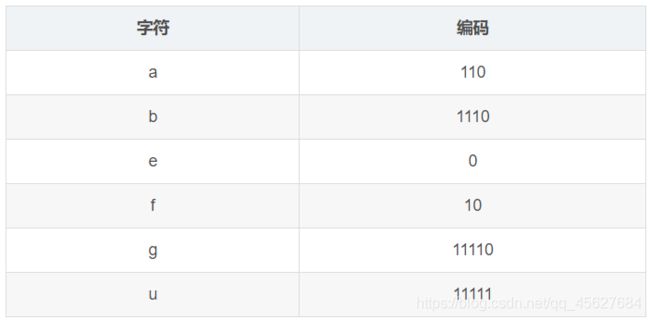
首先,这是我们需要得到的表

即输入一个字符串,我们需要根据字符串得到每个字符的频度,并将这个表存储起来,因为之后要根据这个表来构造哈夫曼树。
所以最适合存储字符的数据结构是结构体,这样就可以将一个字符和其频度存储起来,就像一个表一样。以下为我的结构体
typedef struct ATTRIBUTE {
u8 character;
u32 frequency;
}ATTRIBUTE;
这就是存储一个字符的结构体,分为字符和频度两个部分。
我们知道,所有的字符都是由ASCII码为基的,ASCII码一共有256个,包括所有的可视字符和所有的不可视字符。所以我的想法是,构造一个大小为256的数组,对应着256个ASCII码,这样一个字符串输入进去,可以根据其ASCII码值分别统计,清晰明了。
这是我主函数里定义的实参,通过传参将其传入函数中。
u8 str[128];
u32 ascii[256] = {
0};
u32 characterCount;
以下为生成频度表的代码
ATTRIBUTE *initAttributeList(u8 *str, u32 *ascii, u32 *characterCount) {
u32 i;
u32 index = 0;
u32 count = 0;
ATTRIBUTE *attributeList;
for (i = 0; str[i]; i++) {
ascii[str[i]]++;
}
for (i = 0; i < 256; i++) {
count += (ascii[i] != 0);
}
*characterCount = count;
attributeList = (ATTRIBUTE *) calloc(sizeof(ATTRIBUTE), count);
for (i = 0; i < 256; i++) {
if (ascii[i] != 0) {
attributeList[index].character = (u8) i;
attributeList[index++].frequency = ascii[i];
}
}
return attributeList;
}
str为用户输入的字符串, characterCount为字符种类。因为字符种类在之后的编程中还要用到,所以我直接将它当作一个参数传了进去,这样以后的函数就可以直接使用这个值了。
以上是初始化频度表的内容,既然有初始化,有空间的申请,就必然要有释放。以下为销毁的函数
void destoryAttributeList(ATTRIBUTE *attributeList) {
if (NULL == attributeList) {
return;
}
free(attributeList);
}
编写到这一步,我建议先写一个显示的函数,以判断其正确性。
void showAttributeList(u32 characterCount, ATTRIBUTE *attributeList) {
u32 i;
for (i = 0; i < characterCount; i++) {
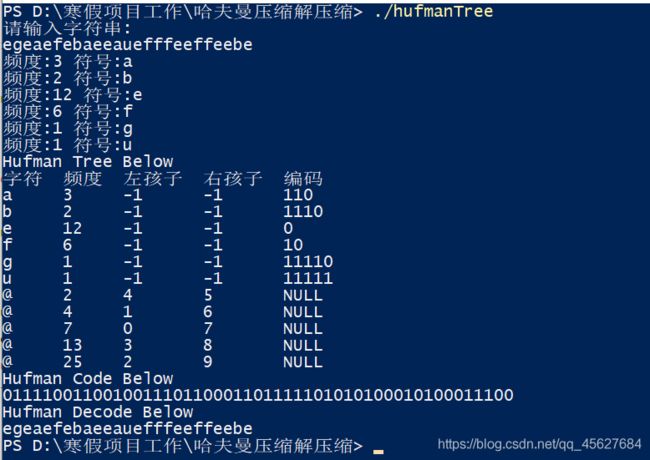
printf("频度:%d 符号:%c\n", attributeList[i].frequency, attributeList[i].character);
}
}
这样,得到频度表便完成了。
b. 生成哈夫曼树
① 初始化节点
一个二叉树的节点由几个信息构成:该节点存储的数据,其左孩子下标,其右孩子下标,其哈夫曼编码。
在后面生成哈夫曼树的过程中,在找最小频度节点时,我需要知道一个节点是否已经参与了构造,所以我除了以上四个信息,还需要知道这个节点是否被访问过。因此我构造的节点的结构体如下
typedef struct HUFMAN_TREE_NODE {
boolean visited;
u8 *hufmanCode;
u32 leftChild;
u32 rightChild;
ATTRIBUTE attribute;
}HUFMAN_TREE_NODE;
所以在生成哈夫曼树之前,我们需要对结构体进行初始化,即对每个结点的初始化。
以下为初始化节点的函数
HUFMAN_TREE_NODE *initHufmanTreeNode(u32 characterCount, u32 *orientate, ATTRIBUTE *attributeList) {
u32 i;
u32 nodeCount;
HUFMAN_TREE_NODE *hufmanTreeNode;
nodeCount = characterCount * 2 - 1;
hufmanTreeNode = (HUFMAN_TREE_NODE *) calloc(sizeof(HUFMAN_TREE_NODE), nodeCount);
for (i = 0; i < characterCount; i++) {
hufmanTreeNode[i].visited = FALSE;
hufmanTreeNode[i].hufmanCode = (u8 *) calloc(sizeof(u8), characterCount);
hufmanTreeNode[i].leftChild = hufmanTreeNode[i].rightChild = -1;
hufmanTreeNode[i].attribute = attributeList[i];
orientate[attributeList[i].character] = i;
}
return hufmanTreeNode;
}
根据之前的公式,我们有characterCount个字符,所以生成的节点数有 characterCount * 2 - 1 个。
有一行代码需要注意,在每次循环的末尾。
orientate[attributeList[i].character] = i;
orientate是我在主函数定义的另一个数组。其意为确定方位。我们将一个符号的ASCII码为下标,将其节点的顺序i作为值存储在这个数组中,之后在编码中,我们就可以直接根据一个符号的ASCII码将其信息提取出来了。
u32 orientate[256] = {
0};
有了初始化,还是和上一个一样,我们需要一个用来释放空间的销毁函数和一个用来判断对错的显示函数。
void showHufmanTreeNode(u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode) {
u32 i;
printf("字符 频度 左孩子 右孩子 编码\n");
for (i = 0; i < characterCount; i++) {
printf("%-5c %-5d %-7d %-7d %-10s\n",
hufmanTreeNode[i].attribute.character,
hufmanTreeNode[i].attribute.frequency,
hufmanTreeNode[i].leftChild,
hufmanTreeNode[i].rightChild,
hufmanTreeNode[i].hufmanCode == NULL ? "NULL" : hufmanTreeNode[i].hufmanCode);
}
}
void destoryHufmanTreeNode(u32 count, HUFMAN_TREE_NODE *hufmanTreeNode) {
u32 i;
if (NULL == hufmanTreeNode) {
return;
}
for (i = 0; i < count; i++) {
free(hufmanTreeNode[i].hufmanCode);
}
free(hufmanTreeNode);
}
② 查找频度最小节点
生成哈夫曼树的过程,我们需要不断查找最小频度的节点,并生成新的节点。所以我们需要先构造一个此功能的函数。
u32 searchMinimumNode(u32 count, HUFMAN_TREE_NODE *hufmanTreeNode) {
u32 i;
u32 minIndex = -1;
for (i = 0; i < count; i++) {
if (FALSE == hufmanTreeNode[i].visited
&& (-1 == minIndex
|| hufmanTreeNode[minIndex].attribute.frequency > hufmanTreeNode[i].attribute.frequency)) {
minIndex = i;
}
}
hufmanTreeNode[minIndex].visited = TRUE;
return minIndex;
}
这个的逻辑还是挺复杂的,大家可以自己想一想。
需要注意的是,在找到最小的结点后,需要将这个结点的visited设为TRUE,这样下次查找,就不会再重复找到已经参与构造的结点了。
③ 哈夫曼树的构造
万事已经具备,现在可以构造哈夫曼树了。仔细考虑之前的过程,其实可以发现构造哈夫曼树的过程逻辑非常简单。
在所有节点里,先找到两个频度最小的节点,然后其频度和生成一个新的节点,重复这个过程。
代码如下
void creatHufmanTree(u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode) {
u32 i;
u32 leftChild;
u32 rightChild;
u32 count = characterCount;
for (i = 0; i < count - 1; i++) {
leftChild = searchMinimumNode(count+i, hufmanTreeNode);
rightChild = searchMinimumNode(count+i, hufmanTreeNode);
hufmanTreeNode[count+i].visited = FALSE;
hufmanTreeNode[count+i].hufmanCode = NULL;
hufmanTreeNode[count+i].leftChild = leftChild;
hufmanTreeNode[count+i].rightChild = rightChild;
hufmanTreeNode[count+i].attribute.character = '@';
hufmanTreeNode[count+i].attribute.frequency =
hufmanTreeNode[leftChild].attribute.frequency +
hufmanTreeNode[rightChild].attribute.frequency;
}
}
生成的父节点的符号我们用’@'来代替。需要注意的是,每次查找最小频度结点,是在所有结点里一起找的,也就是之前新生成的结点,在下一次查找中要参与进去。
所以我的查找函数的参数是count + i ,这样就可以遍历到新生成的结点。
B. 哈夫曼编码
a. 得到每个字符的编码
根据之前我们的手工过程,要得到一个字符的哈夫曼编码,需要根据哈夫曼树,从根节点开始走,一个一个找到字符。找到一个字符就返回到根节点,重新开始走,找下一个字符。这个过程就是一个递归的过程,所以我们用递归来完成这个编码过程。
void creatHufmanCode(u8 *code, u32 index, u32 root, HUFMAN_TREE_NODE *hufmanTreeNode) {
if (-1 == hufmanTreeNode[root].leftChild) {
code[index] = 0;
strcpy(hufmanTreeNode[root].hufmanCode, code);
return;
} else {
code[index] = '0';
creatHufmanCode(code, index+1, hufmanTreeNode[root].leftChild, hufmanTreeNode);
code[index] = '1';
creatHufmanCode(code, index+1, hufmanTreeNode[root].rightChild, hufmanTreeNode);
}
}
对递归很困惑的同学可以去看我的一篇博客,通过一个经典的递归,八皇后问题,对递归进行了分析和讲解。
【C语言基础】->递归调用->八皇后问题
b. 编码
现在我们有了每个字符的哈夫曼编码的表,可以根据这个表以及用户输入的字符串进行编码了。
u8 *coding(u8 *str, u32 *orientate, u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode) {
u8 *code = NULL;
u32 i;
u32 sum = 0;
for (i = 0; i < characterCount; i++) {
sum += hufmanTreeNode[i].attribute.frequency * strlen(hufmanTreeNode[i].hufmanCode);
}
code = (u8 *) calloc(sizeof(u8), sum);
for (i = 0; str[i]; i++) {
strcat(code, hufmanTreeNode[orientate[str[i]]].hufmanCode);
}
return code;
}
这个部分就是之前初始化时orientate这个定位数组的作用。可以根据字符快速找到这个字符对应的哈夫曼编码。
希望大家一定要养成一个习惯,只要有申请空间,就一定要先考虑释放空间。我们对code申请了空间,所以理所当然地要写一个释放它的函数。
void destoryCode(u8 *hufCode) {
if (NULL == hufCode) {
return;
}
free(hufCode);
}
C. 解码
解码和生成哈夫曼编码的过程是类似的,根据我们做的手工过程,从第一个字符开始,如果是0,就向左走,是1就向右走,找到一个字符就从根节点重新开始查找。
u8 *decoding(u8 *hufCode, u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode) {
u8 *decode = NULL;
u32 i;
u32 index = 0;
u32 sum = 0;
u32 father = 2 * characterCount - 2;
for (i = 0; i < characterCount; i++) {
sum += hufmanTreeNode[i].attribute.frequency;
}
decode = (u8 *) calloc(sizeof(u8), sum);
for (i = 0; hufCode[i]; i++) {
if ('0' == hufCode[i]) {
decode[index++] = hufmanTreeNode[hufmanTreeNode[father].leftChild].attribute.character;
father = characterCount * 2 - 2;
} else {
father = hufmanTreeNode[father].rightChild;
if (-1 == hufmanTreeNode[father].leftChild) {
decode[index++] = hufmanTreeNode[father].attribute.character;
father = characterCount * 2 - 2;
}
}
}
return decode;
}
这个过程有一个需要注意的地方,因为u的编码是11111,所以不是每一个叶子结点都是遇到0就到了,我们还需要根据这个结点的子节点判断它是不是已经到了二叉树的末端。
Ⅲ 完整代码&运行结果
首先是tyz.h头文件的内容
#ifndef _TYZ_H_
#define _TYZ_H_
#define TRUE 1
#define FALSE 0
#define NOT_FOUND -1
#define SET(value, index) (value |= 1 << (index ^ 7))
#define CLEAR(value, index) (value &= ~(1 << (index ^ 7)))
#define GET(value, index) (((value) & (1 << ((index) ^ 7))) != 0)
typedef unsigned char boolean;
typedef unsigned int u32;
typedef unsigned short u16;
typedef boolean u8;
int skipBlank(const char *str);
boolean isRealStart(int ch);
boolean isFileExist(const char *filename);
char *creatFilename(const char *sourceFilename, const char *extensionName, char *targetFilename);
#endif
然后是hufmanTree.h头文件的内容
#ifndef _TYZ_HUFMAN_TREE_H_
#define _TYZ_HUFMAN_TREE_H_
#include "tyz.h"
typedef struct ATTRIBUTE {
u8 character;
u32 frequency;
}ATTRIBUTE;
typedef struct HUFMAN_TREE_NODE {
boolean visited;
u8 *hufmanCode;
u32 leftChild;
u32 rightChild;
ATTRIBUTE attribute;
}HUFMAN_TREE_NODE;
ATTRIBUTE *initAttributeList(u8 *str, u32 *ascii, u32 *characterCount);
void destoryAttributeList(ATTRIBUTE *attributeList);
void showAttributeList(u32 characterCount, ATTRIBUTE *attributeList);
HUFMAN_TREE_NODE *initHufmanTreeNode(u32 characterCount, u32 *orientate, ATTRIBUTE *attributeList);
void destoryHufmanTreeNode(u32 count, HUFMAN_TREE_NODE *hufmanTreeNode);
void showHufmanTreeNode(u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode);
void creatHufmanTree(u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode);
u32 searchMinimumNode(u32 count, HUFMAN_TREE_NODE *hufmanTreeNode);
void creatHufmanCode(u8 *code, u32 index, u32 root, HUFMAN_TREE_NODE *hufmanTreeNode);
u8 *coding(u8 *str, u32 *orientate, u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode);
void destoryCode(u8 *hufCode);
u8 *decoding(u8 *hufCode, u32 characterCount, HUFMAN_TREE_NODE *hufmanTreeNode);
#endif
最后是hufmanTree.c的内容
#include Ⅳ 一条重要的小补充
这个代码说到底也只是对字符编码和解码而已,并不是真的对字符串进行了压缩,因为生成的编码仍是字符型,u占一个字节,其编码11111占了5个字节,所以这个可以说是哈夫曼膨胀了。
但是之所以先写这个代码,是因为这个无论是哈夫曼树的生成还是编码解码等过程,都是完成大项目哈夫曼压缩解压缩的一个基础。
在之后的博文里,我会完成哈夫曼压缩解压缩项目,是真的可以将文件压缩然后解压缩的有实际作用的程序。我会用到位运算和文件操作,如果对这两个知识点仍有疑惑的同学可以移步到我的这两个博文。
【C语言基础】->递归调用->八皇后问题
【C语言基础】->位运算详细解析->位运算的使用
【C语言基础】->文件操作详解->一篇文章读懂关于文件的庞杂函数使用
【C语言->数据结构与算法】->树与二叉树概念&哈夫曼树的构造
以下为我的完成版哈夫曼压缩&解压缩
【C语言->数据结构与算法】->哈夫曼压缩&解压缩->终局->压缩率百分之八十六