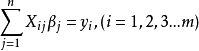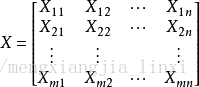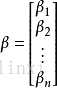智能建模之最小二乘辨识LS：Matlab实现
智能建模之最小二乘辨识LS：Matlab实现
维基百科解释：https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)
百度百科解释：http://baike.baidu.com/link?url=lslmpU3mejdmTa5HFapiYoIeZjLmkznLtH1vkxdU3k6xtz7I0BgxDfNbUPwqiZBR_idDmtkv-dFIakwfs31pF6ZbsAtfTeA4ZI01eh_GM6iCx2_JC6RxNIKRQAKbf32RB22XOv6mcPtP6EfdR_e_Oq
基础知识：
最小二乘法（LS）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，
并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大
化熵用最小二乘法来表达。
考虑超定方程组（超定指未知数小于方程个数）：
其中m代表有m个等式，n代表有 n 个未知数β，m>n ；将其进行向量化后为：
，
，
显然该方程组一般而言没有解，所以为了选取最合适的β让该等式"尽量成立"，引入残差平方和函数S
（在统计学中，残差平方和函数可以看成n倍的 均方误差MSE）
当 
时， 
取最小值，记作：
通过对 
进行微分求最值，可以得到：
如果矩阵 
非奇异则β有唯一解：
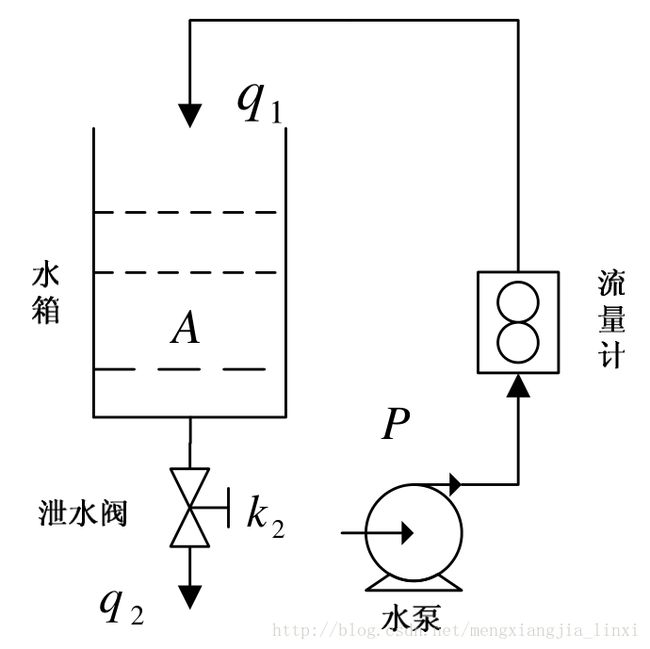
应用：水箱模型辨识
要求：
单容水箱的液位过程的建模：采用系统辨识方法，基于实验数据建立离散时间非线性动态模型。输入变量为入口流量，输出变量为液位。
给定的数据集采样周期为60秒，自己可以划分为训练集和测试集。
这里采用：机理模型辨识（机理模型参数如出口阀流量系数假设未知，需要基于数据学习估计）
机理建模过程：
（都不能直接从word复制过来，所以直接上图吧，说明问题就OK）
即：
Y=φμ (8)（前面有7个~~）
需要辨识：流量系数μ。
最小二乘参数辨识：
matlab代码：
%% 最小二乘辨识流量系数 %
%清除变量空间；关闭所有窗口
clear all;close all;clc;
%读取、处理数据
data=xlsread('水箱数据.xlsx'); %80组数据（80*2）
IN=data(:,1); %data的第一列数据
OUT=data(:,2); %data的第二列数据
%创建相关数组
L=40; %取40组辨识，剩下40组测试
phi=zeros(L,1);
Y=zeros(L,1);
Y_test=zeros(L,1);
Y_real=zeros(L,1);
A=0.01767; %水箱横截面积
h=OUT./100; %所有数据除以100换算单位：cm->m
Q=IN.*10^-5; %流量单位换算：L/min -> 立方米/分
% 要辨识的参数θ（theta）；公式：Y=φ*θ（Y=phi*theta）
for k=1:L
%公式（8）
phi(k,1)=-sqrt(h(k))/A;
Y(k)=h(k+1)-h(k)-Q(k)/A;
end
% 关键公式：得到辨识参数
theta=inv(phi'*phi)*phi'*Y
%% 辨识模型验证 %
for k=1:L
Y_test(k)=h(L+k-1) - theta*sqrt(h(L+k-1))/A + Q(L+k-1)/A; %一步预测值
Y_real(k)=h(L+k); %真实值
end
%% 画图 %
plot([1:L],Y_real,'b',[1:L],Y_test,'r'); %横坐标-纵坐标-颜色；横坐标-纵坐标-颜色
xlabel('时间/min');
ylabel('液位/m');
legend('真实值','预测值');
title('最小二乘辨识水箱机理模型');
%% 辨识精度指标 %
%RMSE（均方根误差）；MAPE（平均绝对百分比误差）
RMSE = sqrt((sum((Y_test-Y_real).^2))/L);
MAPE = sum(abs((Y_test-Y_real)./Y_real))/L;
[RMSE,MAPE]运行结果：
theta =
-1.1533e-04
ans =
0.0018 0.0097
使用实际水箱模型的另外40组无关数据，对上式所示模型进行测试，结果如下。
采用如下所示的性能评价指标均方根误差(RMSE)和平均绝对百分比误差(MAPE)对上图所示模型测试结果进行评价
求得RMSE=0.0018， MAPE=0.0097。
附录：
水箱数据：
输入：流量L/min；输出：液位cm
（将下列数据放入excel文件）水箱数据.xlsx
第一列：
流量（L/min）
1.529
1.602
1.66
1.683
1.702
1.736
1.759
1.783
1.796
1.816
1.837
1.852
1.879
1.901
1.913
1.931
1.946
1.963
1.976
1.998
2.037
2.09
2.111
2.124
2.131
2.141
2.156
2.161
2.167
2.173
2.185
2.194
2.203
2.21
2.227
2.256
2.271
2.286
2.313
2.339
2.341
2.349
2.352
2.367
2.371
2.378
2.381
2.388
2.396
2.402
2.417
2.435
2.444
2.452
2.457
2.462
2.47
2.481
2.491
2.496
2.502
2.507
2.513
2.522
2.536
2.55
2.571
2.581
2.587
2.589
2.633
2.674
2.873
3.087
3.122
3.173
3.3
3.502
3.717
3.966
第二列：
液位（cm）
0.5
0.6
0.7
0.8
0.9
1
1.2
1.3
1.5
1.6
1.7
1.8
1.9
2
2.2
2.4
2.5
2.7
2.9
3.2
4.4
5
5.3
5.4
5.5
5.7
6.2
6.3
6.4
6.5
6.8
7.2
7.6
8.2
8.5
9
9.2
9.6
9.6
9.9
10.1
10.3
10.5
10.8
11.1
11.5
11.6
11.7
12.1
12.4
12.7
12.9
13.2
13.5
13.8
14.1
14.3
14.6
14.9
15.1
15.3
15.7
16
16.4
16.8
17
17.2
17.5
17.7
18
18.2
18.4
18.6
18.8
19
19.3
19.5
19.6
19.8
20
结束~