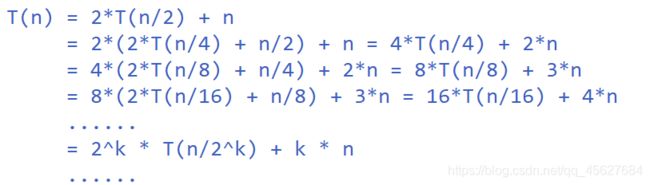【数据结构与算法】-＞算法-＞排序（二）-＞归并排序&快速排序

Ⅰ 前言

在排序（一）中，我给了一个表

第二节我们就来看看时间复杂度为 O(nlog₂n) 的两个算法，归并排序以及快速排序。第一节的排序可以从下面的链接跳转过去。

【数据结构与算法】-＞算法-＞排序（一）-＞冒泡排序&插入排序&选择排序

Ⅱ 归并排序（Merge Sort）

1. 详解

归并排序其实我在我程序员必修数学课里已经写过一次，并详细分析了分治思想，有兴趣的同学可以跳转过去，这里再把我对归并排序的讲解搬过来。

【程序员必修数学课】-＞基础思想篇-＞递归（下）-＞分而治之&从归并排序到MapReduce

归并排序算法的核心就是“归并”，也就是把两个有序的数列合并起来，形成一个更大的有序数列。

假设我们需要按照从小到大的顺序，合并两个有序数列 A 和 B。我们需要开辟一个新的存储空间 C，用于保存合并后的结果。

我们首先比较两个数列的第一个数，如果 A 数列的第一个数小于 B 数列的第一个数，那么就先取出 A 数列的第一个数放入 C，并把这个数从 A 数列中删除。如果是 B 的第一个数更小，那么就先取出 B 数列的第一个数放入 C，并把它从 B 数列里删除。

以此类推，直到 A 和 B 里所有的数据都被取出来放入 C。如果到某一步， A 或 B 数列为空，那直接将另一个数列的数据依次取出放入 C 就可以了。这种操作，可以保证两个有序的数列 A 和 B 合并到 C 之后，C 数列仍然是有序的。

比如说合并有序数组 {6, 11, 13, 17} 和 {8, 10, 16}的过程

为了保证得到有序的 C 数列，我们必须保证参与合并的 A 和 B 也是有序的。但是，等待排序的数组一开始都是乱序的，如果无法保证这点，那归并又有什么意义呢？

这就需要用到递归了。我们可以利用递归的思想，把问题不断简化，也就是把数列不断简化，一直简化到最后只有一个数，那它本身就是有序的了。那么如何进行每一次的简化呢？

最简单的想法就是把长度为 n 的数列，每次简化为长度为 n - 1 的数列，直至长度为 1。不过，这样的处理没有并行性，要进行 n - 1 次的归并操作，效率就会很低。

所以，我们可以在归并排序中引入了分而治之（Divide and Conquer） 的思想。分而治之，我们通常简称为分治。它的思想就是，将一个复杂的问题，分解成两个甚至多个规模相同或类似的子问题，然后对这些子问题再进一步细分，直到最后的子问题变得简单，很容易就能被求解出来，这样这个复杂的问题就求解出来了。

归并排序通过分治的思想，把长度为 n 的数列，每次简化为两个长度为 n / 2 的数列。这样更有利于计算机的并行处理，只需要 log₂n 次归并。

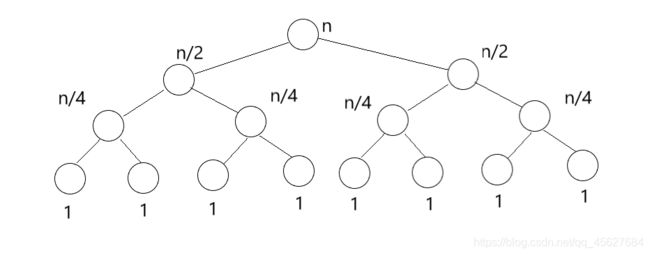
我们把归并和分治的思想结合起来，这其实就是归并排序算法。这种算法每次把数列进行二等分，直到唯一的数字，也就是最基本的有序数列。然后从这些最基本的有序数列开始，两两合并有序的数列，直到所有的数字都参与了归并排序。

我用一个包含 0~9 这 10 个数字的数组，分析一下归并排序的过程。

• 假设初始的数组为 {7, 6, 2, 4, 1, 9, 3, 8, 0, 5}，我们要对它进行从小到大的排序。
• 第一次分解后，变成两个数组 {7, 6, 2, 4, 1} 和 {9, 3, 8, 0, 5}。
• 然后，我们将 {7, 6, 2, 4, 1} 分解成 {7, 6} 和 {2, 4, 1}，将 {9, 3, 8, 0, 5} 分解成 {9, 3} 和 {8, 0, 5}。
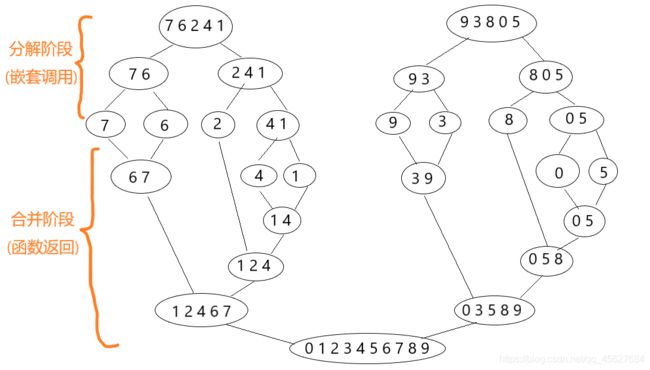
• 按照这个规律继续细分下去，直到每个组只包含一个数字。到这里，都是递归的嵌套调用过程。
• 接下来，就要开始进行合并了。我们可以将 {4, 1} 分解为 {4} 和 {1}。现在无法再细分了，我们开始合并，在合并的过程中进行排序，所以合并的结果为 {1, 4}。合并后的结果将返回当前函数的调用者，这就是函数返回的过程。
• 重复上述合并的过程，直到完成整个数组的排序，得到 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。

这个过程可以画一张图来理解

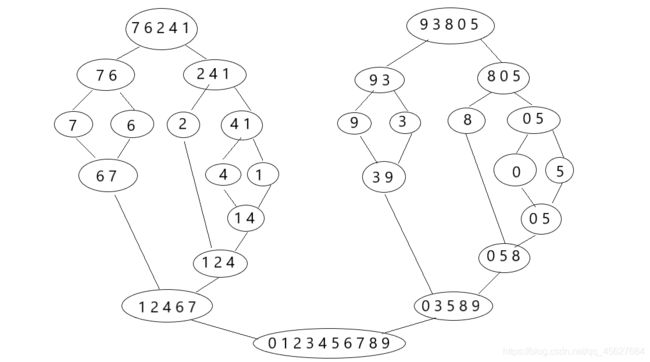
可以看到 归并排序使用了分治的思想，而这个过程需要使用递归来实现。

归并排序算法用分治的思想把数列不断地简化，直到每个数列仅剩下一个单独的数，然后再使用归并逐步合并有序的数列，从而达到将整个数列进行排序的目的。而这个归并排序，正好可以使用递归的方式来实现。我们可以看看下面这张图，可以发现，分治的过程和递归的过程是一致的。

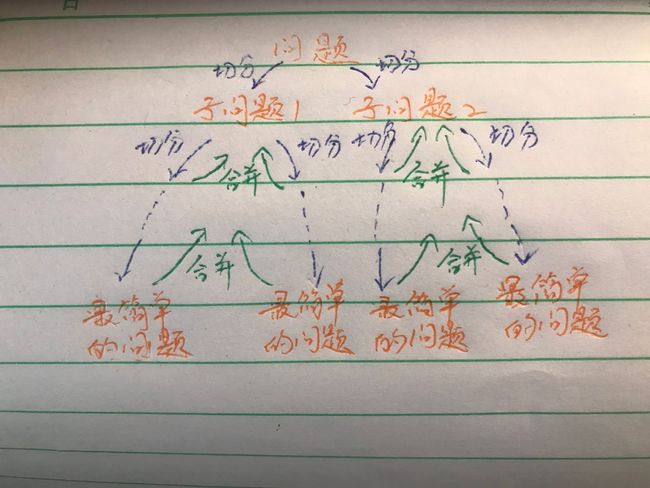
分治的过程可以通过递归来表达，因此，归并排序最直观的实现方式就是递归。所以，我们从递归的步骤出发，来看归并排序如何实现。

我们假设 n = k - 1 的时候，我们已经对较小的两组数进行了排序。那我们只要在 n = k 的时候，将这两组数合并起来，并且保证合并后的数组仍然是有序的就行了。

所以，在递归的每次嵌套调用中，代码都将一组数分解成更小的两组，然后将这两个小组的排序交给下一次的嵌套调用。而本次调用只需要关心，如何将排好序的两个小组进行合并。

在初始状态，也就是 n = 1 的时候，对于排序的案例而言，只包含单个数字的分组。由于分组里只有一个数字，所以它已经是排好序的了，之后就可以开始递归调用的返回阶段。

现在我用Java简单实现一下归并排序。

package com.tyz.merge_sort.core;

import java.util.Arrays;

public class MergeSort {
     
	
	/**
	 * 合并两个已经排好序的数组（从小到大）
	 * @param arrOne
	 * @param arrTwo
	 * @return
	 */
	private static int[] merge(int[] arrOne, int[] arrTwo) {
     
		if (arrOne == null) {
     
			return new int[] {
     };
		}
		if (arrTwo == null) {
     
			return new int[] {
     };
		}
		int[] mergedArr = new int[arrOne.length + arrTwo.length];
		
		int mi = 0;
		int ai = 0;
		int bi = 0;
		
		while (ai < arrOne.length && bi < arrTwo.length) {
     
			if (arrOne[ai] < arrTwo[bi]) {
     
				mergedArr[mi] = arrOne[ai];
				ai++;
			} else {
     
				mergedArr[mi] = arrTwo[bi];
				bi++;
			}
			mi++;
		}
		
		if (ai < arrOne.length) {
     
			for (int i = ai; i < arrOne.length; i++) {
     
				mergedArr[mi] = arrOne[i];
				mi++;
			}
		} else {
     
			for (int i = bi; i < arrTwo.length; i++) {
     
				mergedArr[mi] = arrTwo[i];
				mi++;
			}
		}
		
		return mergedArr;
	}
	
	/**
	 * 使用递归实现归并排序
	 * @param arr
	 * @return
	 */
	 public static int[] mergeSort(int[] arr) {
     
		 if (arr == null) {
     
			 return new int[] {
     };
		 }
		 if (arr.length == 1) {
     
			 return arr;
		 }
		 int middle = arr.length / 2;
		 int[] left = Arrays.copyOfRange(arr, 0, middle);
		 int[] right = Arrays.copyOfRange(arr, middle, arr.length);
		 
		 left = mergeSort(left);
		 right = mergeSort(right);
		 
		 int[] mergedArr = merge(left, right);
		 
		 return mergedArr;
	 }
}

测试代码如下

package com.tyz.merge_sort.test;

import com.tyz.merge_sort.core.MergeSort;

public class Test {
     

	public static void main(String[] args) {
     
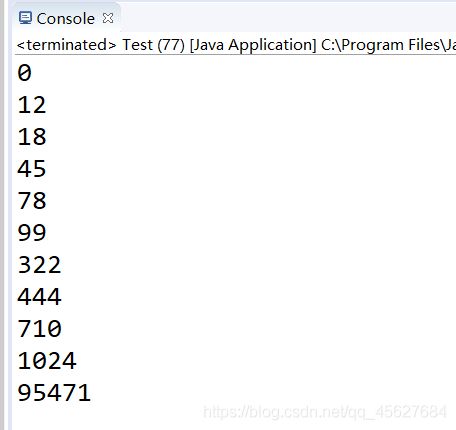
		int[] arr = {
     78, 12, 444, 710, 18, 322, 0, 45, 95471, 99, 1024};
		int[] sorted = MergeSort.mergeSort(arr);
		
		for (int i = 0; i < sorted.length; i++) {
     
			System.out.println(sorted[i]);
		}
	}

}

结果如下

2. 归并排序稳定性

结合前面我画的图还有代码，我们可以判断出来，归并排序稳定不稳定关键要看 merge() 函数，也就是两个有序子数组合并成一个有序数组的那部分代码。

在合并的过程中，如果 A[p...q] 和 A[q+1...r] 数组之间有值相同的元素，那我们可以先把 A[p...q]中的元素放入临时数组中，这样就保证了值相同的元素，在合并前后的先后顺序不变。所以，归并排序是一个稳定的排序算法。

3. 归并排序时间复杂度

归并排序涉及递归，时间复杂度的分析比较复杂，我们来逐步推导一下。

我们知道递归的适用场景是，一个问题 a 可以分解为多个子问题 b、c，那求解问题 a 就可以分解为求解问题 b、c。问题 b、c 解决之后，我们再把 b、c 的结果合并成 a 的结果。

如果我们定义求解问题 a 的时间是 T(a)，求解问题 b、c 的时间分别是 T(b) 和 T©，那我们就可以得到这样的递推关系式。

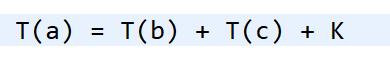
其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。

因此我们可以得到一个重要的结论，不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递推公式。

套用这个式子，我们来分析一下归并排序的时间复杂度。

我们假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。我们知道，merge()函数合并两个有序子数组的时间复杂度都是 O(n)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是：

我们再进一步分解一下计算过程。

通过这样一步一步分解推导，我们可以得到

T(n) = 2^k * T(n/2^k) + k * n

当 T(n/2^k) = T(1) 时，也就是 n/2^k = 1，我们得到 k = log₂n。我们将 k 值代入上面的公式，得到 T(n) = C*n + nlog₂n。如果我们用大 O 标记法来表示的话， T(n) 就等于 O(nlog₂n)。所以归并排序的时间复杂度就是 O(nlog₂n)。

我们从原理分析和代码可以看出，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况，还是最坏情况，或者平均情况，时间复杂度都为 O(nlog₂n)。

4. 归并排序空间复杂度

归并排序的时间复杂度任何情况下都是 O(nlog₂n)，但是归并排序并没有像快排一样，应用广泛，因为它有一个致命的弱点，就是归并排序不是原地排序算法。

这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。那么归并排序的空间复杂度到底是多少呢？是 O(n) ，还是 O(nlog₂n)，我们要怎么分析呢？

如果我们继续按照分析递归时间复杂度的方法，通过递推公式来求解，那整个归并过程需要的空间复杂度就是 O(nlog₂n)。不过，类似分析时间复杂度那样来分析空间复杂度，是不对的。

实际上，递归代码的空间复杂度并不能像时间复杂度那样累加。尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就是只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据大小，所以归并排序空间复杂度是 O(n)。

Ⅲ 快速排序（Quicksort）

1. 详解

我们习惯性地把快速排序算法简称为“快排”，快排利用的也是分治思想。乍看起来，它有点像归并排序，但是思路其实完全不一样。

快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

我将这个递归写成Java程序，大家可以对照着看一看。

private static void quickSort(int[] arr, int start, int end) {
     
		if (start >= end) {
     
			return;
		}
		int pivot = partition(arr, start, end);	//获取分区点
		quickSort(arr, start, pivot - 1);
		quickSort(arr, pivot + 1, end);
	}
	
	public static void quickSort(int[] arr) {
     
		quickSort(arr, 0, arr.length - 1);
	}

归并排序中有一个 merge() 合并函数，我们这里有一个 partition() 分区函数。partition() 分区函数就是随机选择一个元素作为 pivot（一般情况下，可以选择 p 到 r 区间的最后一个元素），然后对 A[p...r]分区，函数返回 pivot 的下标。

如果我们不考虑空间消耗的话，partition() 分区函数可以写得非常简单。我们申请两个临时数组 C 和 B，遍历 A[p...r]，将小于 pivot 的元素都拷贝到临时数组 B，将大于 pivot 的元素都拷贝到临时数组 C，最后再将数组 B 和数组 C 中数据顺序拷贝到 A[p...r]。

但是，如果按照这种思路实现的话，partition() 分区函数就需要很多额外的内存空间，快排就不是原地排序了。如果我们希望快排是原地排序算法，那它的空间复杂度得是 O(1)，那 partition() 分区函数就不能占用太多额外的内存空间，我们就需要在 A[p...r]的原地完成分区操作。

原地分区函数的实现思路非常巧妙，我贴在下面，大家可以看看。简直要说一声 wow。

private static int partition(int[] arr, int start, int end) {
     
		int pivot = arr[end];
		int i = start;
		int temp;
		
		for (int j = start; j < end; j++) {
     
			if (arr[j] < pivot) {
     
				temp = arr[i];
				arr[i] = arr[j];
				arr[j] = temp;
				i++;
			}
		}
		temp = arr[i];
		arr[i] = arr[end];
		arr[end] = temp;
		
		return i;
	}

相信你看完这段代码，还是云里雾里的，并没有 wow 的一声叫出来，下面我用一个图解，来说明这个找区分点的过程。这里还是借用一下王争老师的图，他课程里的图实在是太清晰了。

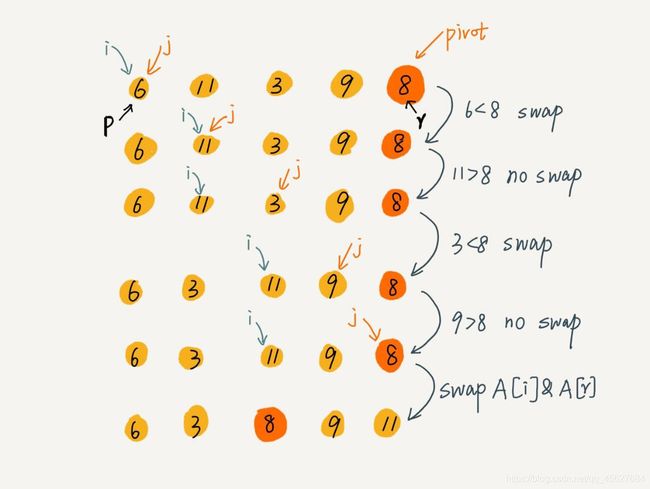
图里的swap，就是交换两个值的意思，对应着代码里的这几步操作

		temp = arr[i];
		arr[i] = arr[j];
		arr[j] = temp;
		i++;

图中的 A[r] 就对应着我的代码里的 A[end]。

相信你认真跟一边这个图，就会感受到这个原地分区的精妙了。

这里的处理有点类似选择排序，我们通过游标 i 把 A[p...end-1]分成了两部分，A[p...i-1]的元素都是小于 pivot 的，我们暂且叫它 “已处理区间”，A[i...end-1]是“未处理区间”。我们每次都从未处理的区间 A[i...end-1]中取一个元素 A[j]，与 pivot 对比，如果小于 pivot，则将其加入到已处理区间的尾部，也就是 A[i]的位置。

2. 快速排序稳定性

因为分区的过程涉及交换操作，如果数组中有两个相同的元素，那么再经过一次分区操作之后，先后顺序就会改变，所以快速排序不是一个稳定的排序算法。

3. 快速排序时间复杂度

快排也是用递归来实现的，对于递归代码的时间复杂度，我前面写的公式这里也是适用的。

如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递推求解公式跟归并是相同的，所以，快排的时间复杂度也是 O(nlog₂n)。

但是，公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。

如果一个数组中的数据原来已经是有序的了，比如 1，3，4，5，6。如果每次选择最后一个元素作为 pivot ，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素，这种情况下，快排的时间复杂度就从 O(nlog₂n) 退化成了 O(n²)。

刚才说的这两个极端情况下的时间复杂度，一个是分区极其均衡，一个是分区极其不均衡。它们分别对应快排的最好情况时间复杂度和最坏时间复杂度。那快排的平均情况时间复杂度是多少呢？

我们假设每次分区操作都将区间分成大小为 9 : 1 的两个小区间。我们继续套用递归时间复杂度的递推公式，就会变成这样

这个公式的递推求解的过程非常复杂，可以求解，但是并不推荐这样做。实际上，递归的时间复杂度的求解方法除了递推公式之外，还有递归树，这个在我之后的关于树文章里会讲到。

我们可以直接在这里有个结论：快排在大部分情况下的时间复杂度都可以做到 O(nlog₂n)，只有在极端情况下，才会退化到 O(n²)。

4. 快速排序空间复杂度

这个在解释原理的时候我们已经说过了，快速排序是一个原地排序，空间复杂度为 O(1)。

Ⅳ 补充

1. 归并排序和快速排序的区别

之前的学习中，我们很容易发现，归并和快排用的都是分治思想，递推公式和递归代码也非常相似，那它们的区别在哪里？

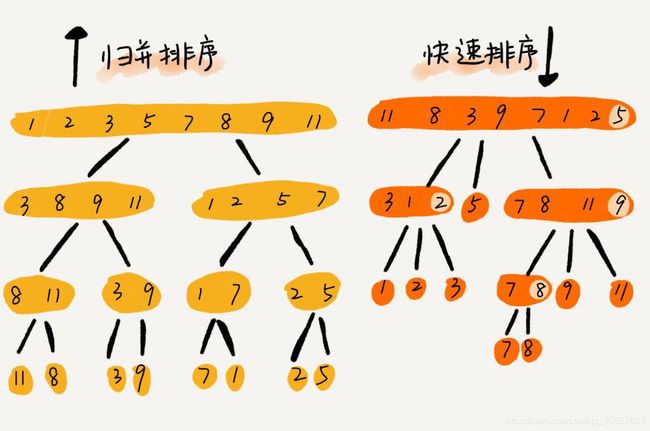
可以发现，归并排序的处理过程是自下而上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是自上而下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlog₂n) 的排序算法，但是它并非是原地排序算法。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

2. O(n) 时间复杂度内求无序数组中的第K大元素

快排的核心思想就是分区和分治，我们可以利用分区的思想，来解决这个问题。比如 4， 2， 5， 12， 3 这样一组数据，第 3 大元素就是 4 。

我们选择数组区间 A[0...n-1]的最后一个元素 A[n-1]作为 pivot，对数组 A[0...n-1]原地分区，这样数组就分成了三部分，A[0...p-1]、A[p]、A[p+1...n-1]。

如果 p + 1 = K，那 A[p]就是要求解的元素；
如果 p + 1 < K，说明第 K 大元素出现在A[p+1...n-1]区间，我们再按照上面的思路递归地在 A[p+1...n-1] 这个区间内查找。
同理，如果 p + 1 > K，那我们就在 A[0...p-1] 这个区间里找。

我们再来看，为什么上述解决问题的思路时间复杂度是 O(n)。

第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。以此类推，分区遍历元素的个数分别为：n/2、n/4、n/8、n/16…直到区间缩小为 1.

如果我们把每次分区遍历的元素个数加起来，就是 n + n/2 + n/4 + … + 1。这是一个等比数列求和，最后的和等于 2n-1。所以，上述解决思路的时间复杂度就为 O(n)。