字符串匹配1———单模式匹配（BF，RK，Sunday，BM，KMP）

前言

字符串匹配（String Match）是计算机行业笔试面试常见的题型，无论是在大公司的笔试真题中，还是在面试中，都是大公司和面试官们津津乐道的话题。
当然字符串匹配也具有一定的难度，特别是讲到后面一些比较复杂难懂的算法例如KMP算法，BM算法等，初学者可能一时之间没办法全部理解，多看几遍，总会孰能生巧的。
字符串匹配的博客，理论讲解部分我分为两篇来写，分别是单模式字符串匹配和多模式字符串匹配。后续有时间 会针对一些习题 应用场景加以表述。

现在开始南国这篇博客的正文，本篇博文内容比较多，但是爱学习的你看完一定会有所收获，Just trust me~

单模式匹配

单模式字符串匹配就是一个字符串a和另一个字符串b进行匹配，一般而言，a的长度远大于b，我们在a中查找是否包含b。我们将字符串a称为主串，字符串b称为模式串。

1.暴力匹配的算法BF算法

BF算法成为暴力匹配算法，又叫做朴素匹配算法。也是最简单的，我们经常用到的算法。最简单的方法就是每次比对m个字符，最坏情况下比较n-m+1次，BF算法的最坏情况时间复杂度为O(n*m)。

BF算法的Java代码实现：

int Search(String S, String T) {　　
　　　int i = 0;
	　　int j = 0;　　
	　　while(i

2.RK算法（基于哈希算法的BF算法优化方案）

RK算法是在BF算法的基础上进行改进，在字符串匹配时加入哈希算法的思想。
RK 算法的思路：我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等，则说明对应的子串和模式串匹配了。
不过，对于这种在字符串中加入哈希算法的思想在具体的实现方案上还有一些地方需要考虑。

问题1.通过哈希算法计算子串的哈希值时候，我们需要遍历子串中的每个字符。尽管模式串与子串比较的效率提高了，但是算法整体的效率并没有提高。有没有方法可以提高哈希算法计算子串哈希值的效率呢？？

问题2：利用到哈希算法，我们就会自然想到哈希函数和散列冲突。前面问题1的解答中南国讲述了一种哈希函数的处理放肆。但是如果字符串中包含的字符不仅仅限于小写字母，还包含大写字母 数字等等ASCII码中的其他字符了。况且当模式串b特别长时，计算的哈希值操作Int的数值范围了。
解决方法是：极端情况下（万一包含的字符是ASCII中126个有效字符），将哈希值的类型设置为Long型 或者Long Long型，那字符串中每个字符对应的ACII码值相加的和作为哈希值。

• 如果两个子串的哈希值不等，则两个子串肯定不相同。
• 如果两个子串的哈希值相同，则在比较目标子串本身（避免哈希冲突带来的误报）

性能分析

整个RK算法的时间复杂度分析我们分为两个部分，计算每个子串的哈希值和子串的哈希值之间的比较。代码中循环复杂度O(n)，hash结果相等时的逐字符匹配复杂度为O(m)，整体时间复杂度为O(m+n)。空间复杂度为O(1)
结论：RK算法的时间复杂度时O(n+m)
RK算法java代码实现：

package StringMatch;

/**
 * RK算法
 * @author xjh 2018.12.29
 */
public class RK {
    public static final int HASHSIZE=100001;
    public static void main(String[] args) {
        String str1 = "searching substring abcddd abcdefg";
        String str2="abcdef";
        System.out.println(Search(str1.toCharArray(),str2.toCharArray()));
    }
    public static int Search(char[] s,char[] p){
        int n=s.length,m=p.length;
        if (m > n || m == 0 || n == 0)
            return -1;
        // sv为S子串的hash结果，pv为字符串p的hash结果，base为x的m-1次方
         long sv = (s[0]), pv = (p[0]), base = 1;
        int i, j;
        // 初始化 sv, pv, base
        for (i = 1; i < m; i++) {
            pv = (pv * 10 + (p[i])) % HASHSIZE;
            sv = (sv * 10 + (s[i])) % HASHSIZE;
            base = (base * 10) % HASHSIZE;
        }
        i = m - 1;
        
        do {
            // 情况一、hash结果相等
            if (sv == pv) {
                for (j = 0; j < m && s[i - m + 1 + j] == p[j]; j++);
                if (j == m)
                    return i - m + 1;
            }
            i++;
            if (i >= n)
                break;
            // O(1)时间更新S子串的hash结果
            sv = (sv + (s[i - m]) * (HASHSIZE - base)) % HASHSIZE;
            sv = (sv * 10 + (s[i])) % HASHSIZE;
        } while (i < n);
        return -1;

    }
}

3.Sunday算法

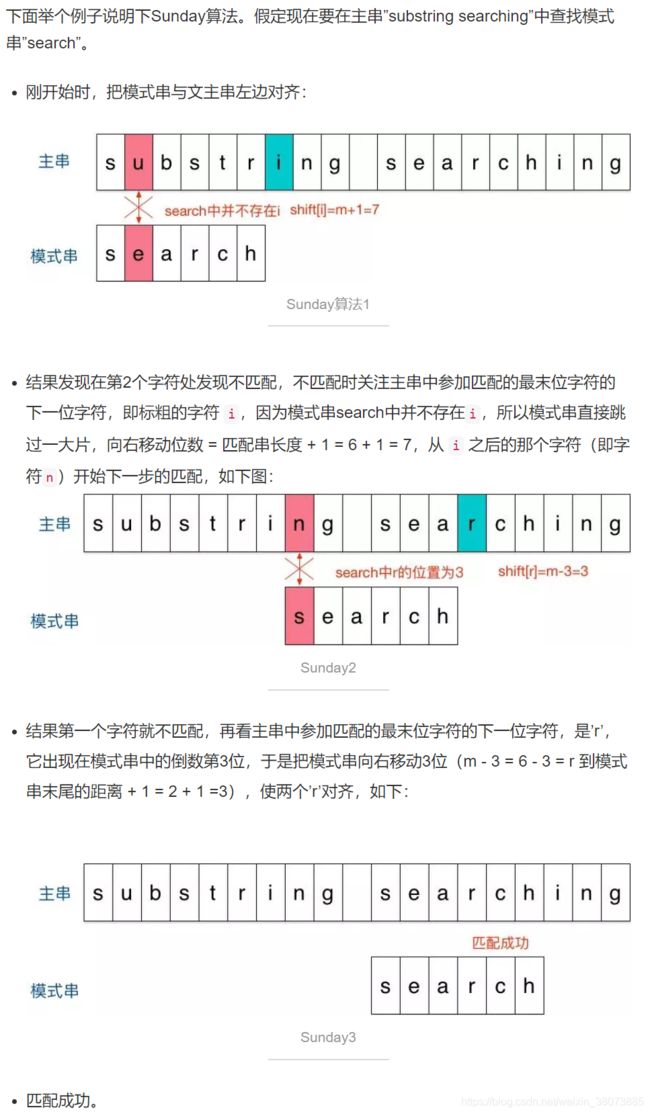
Sunday算法是主串a和模式串b从前往后匹配，在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。
如果该字符没有在模式串中出现则直接跳过，即移动位数 = 模式串长度 + 1；
否则，其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。

Sunday算法的java代码实现：

public static final int ASCII_SIZE=126;
    public static int sunday(char[] a,char[] b){
        int[] move=new int[ASCII_SIZE];
        //主串参与匹配最末位字符移动到该位需要一定的位数       
        for (int i=0;i

4.BM算法

小结：BM算法的核心思想就是利用主串和模式串在匹配过程中的坏后缀 好后缀原则，当主串和模式串发生不匹配时，能够跳过一些不必要的比较过程。后面还会将讲一个KMP算法，它与BM算法在很多地方十分相似。

性能分析

BM算法的平均时间复杂度O(n),它属于典型空间换时间的算法。
在整个算法中，他需要用到额外的3个数组，其中bc数组的大小和字符集大小有关，suffix数组和prefix数组的大小和模式串长度有关。

BM算法的代码实现：

package StringMatch;
/**
 * 字符串匹配算法
 *
 * @author xjh 2018.12.25
 */
public class BM {
    private static final int SIZE = 256;
    /**
     * 利用散列表存储存储模式串中的每个字符及其下标
     */
    private void generateBC(char[] b, int m, int[] bc) {
        for (int i = 0; i < SIZE; i++)
            bc[i] = -1;   //初始化散列表
        for (int i = 0; i < m; i++) {
            int ascii = (int) b[i];    //计算b[i]的ASCII值
            bc[ascii] = i;
        }
    }

    /**
     * 坏字符和好后缀结合使用
     */
    public int bm(char[] a, int n, char[] b, int m) {
        int[] bc = new int[SIZE]; //用来记录模式串中每个字符最后出现的下标
        generateBC(b, m, bc); //构建坏字符哈希表
        int[] suffix = new int[m];
        boolean[] prefix = new boolean[m];
        generateGS(b, m, suffix, prefix);

        int i = 0;    //i表示主串与模式对齐的第一个字符
        while (i <= n - m) {
            int j;
            for (j = m - 1; j >= 0; j--) {
                //模式串从后往前进行匹配
                if (a[i + j] != b[j]) break;    //找到坏字符对应模式串中的下标是j
            }
            if (j < 0) return i;//匹配成功，返回主串与模式串第一个匹配的字符下标
            //这里等同于将模式串视窗往后滑动j-bc[（int）a[i+j]]位
            int x = i + (j - bc[(int) a[i + j]]);
            int y = 0;
            if (j < m - 1) {
                //如果有好后缀的话
                y = moveGS(j, m, suffix, prefix);
            }
            i += Math.max(x, y);
        }
        return -1;
    }

    /**
     * 好后缀原则
     */
    private int moveGS(int j, int m, int[] suffix, boolean[] prefix) {
        //j表示坏字符对应的模式串中的字符下标，m表示模式串长度
        int k = m - 1 - j; //好后缀长度
        if (suffix[k]!=-1) return j-suffix[k]+1;
        for (int r=j+2;r<=m-1;r++){
            if (prefix[m-r]==true) return r;
        }
        return m;
    }

    /**
     * 好后缀原则
     */
    public void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
        //b是模式串，m表示长度
        //suffix 数组的下标 k，表示后缀子串的长度，下标对应的数组值存储的是在模式串中和好后缀匹配的子串{u*}的其实下标值
        //为了避免滑动过多，suffix[]中存储的是模式串中最靠后的那个子串的起始位置，换而言之是下标最大的那个子串起始位置
        //prefix数组用来记录模式串中的后缀子串是否能匹配模式串的前缀子串
        for (int i = 0; i < m; i++) {
            //初始化
            suffix[i] = -1;
            prefix[i] = false;
        }
        for (int i = 0; i < m - 1; i++) {
            //b[0,i]
            int j = i;
            int k = 0;   //k是公共后缀子串
            while (j >= 0 && b[j] == b[m - 1 - k]) {
                //与b[1,m-1]求公共后缀子串
                --j;
                ++k;
                suffix[k] = j + 1;  //j+1白哦是公共后缀子串在b[0,i]中的起始下标
            }
            if (j == -1) prefix[k] = true;  //如果公共后缀子串也是模式串的前缀子串
        }
    }
}

5.KMP算法

小结：KMP算法的思想和BM算法有些类似。KMP算法或许有些人在本科时期就已经接触学习过，南国当年也是怎么也看不明白next数组是怎么一回事。废了好大的劲取理解next数组的构造。
KMP算法的性能分析：
KMP算法的时间复杂度是O(m+n),空间复杂度是O(m)[需要额外申请一个和模式串相同内存大小的数组]

KMP的java代码实现：

package StringMatch;

/**
 * KMP算法 有些难！！ 多看几遍
 * 难点在于构建next数组
 * @author xjh 2018.12.26
 */
public class KMP {
    /**
     * kmp算法
     */
    public static int kmp(char[] a,int n,char[] b,int m){
        //a,b分别是主串和模式串；n,m分別是主串和模式串的长度
        int[] next=getNexts(b,m);
        int j=0;
        for (int i=0;i0&&a[i]!=b[j]) { //一直找到主串和模式串中不匹配的坏字符 也就是a[i]和b[j]
                j=next[j-1]+1;
            }
            if (a[i]==b[j]) ++j;
            if (j==m) return i-m+1;     //找到匹配模式串的了
        }
        return -1;
    }

    /**
     * 构建next数组
     */
    public static int[] getNexts(char[] b,int m){
        //b表示模式串，m表示模式串的长度
        int[] next=new int[m];
        next[0]=-1;
        int k=-1;
        for (int i=1;i

文章小结：

这篇博客关于字符串的单模式匹配问题，我写了5个算法。从浅到深，你会发现后买你的算法越来越难 页越来越不好理解。关于BM算法和KMP算法，在文中我大量用了我自己日常在极客时间有偿报的一门课程，那个老师的文字总结比较全面 对于抽象的东西便于理解一点。
有人会问，看了这么多 脑子都不够用 一头雾水 都有点懵？ 现在的编程语言对于字符串匹配的算法集成的还不够好吗，为什么要花这么长的篇幅 去写这个了？ 在我们的日常工作学习中这些算法应用的多吗？ 有什么应用场景？花这么长的时间学习这个值得吗？？
关于这类的问题了，南国想说 计算机的有些算法深入之后 确实有些难度 想要初学者一下子搞懂 确实也不现实。如果你现在问我，我写的这5个算法 现在给别人上课 或者面试官讲一遍原理和剖析，说实话 南国也不一定能百分百讲的让大家全都明白透彻。而且，南国也了解到一些好学校的acm校队（比如说湖大这种985高校 亦或者是杭电这种强调算法知识竞赛的学校），校队的大牛们经常刷各种算法题 对于一些复杂算法题都会有自己的代码模板 或者算法基本架构。学习本就是一个温故而知新的过程，如果你一遍没太看懂，不是赶着立马要笔试面试 就过段时间再看一遍，到时候你肯定也会有更深一点的理解。
在文章的一开头，我讲过字符串匹配是笔试面试的常考题，所以这篇博客的定位本就不是零基础 入门，如果你能大概懂得这几个算法的原理和剖析，这对你理解某一门百年城语言(java c++)的底层知识都是有莫大的帮助。就好像如果你明白了哈希算法和散列表，那么对于你理解java中HashMap的原理和一些面试场考的知识点将会非常快。关于哈希算法和散列表这块，我之前已经写过一些博文，有兴趣的同学可以查阅。算法和数据结构

一点学习的笔记和收获，愿和大家讨论分享，如果有文章中有不对的地方，欢迎大佬留言交流讨论。
参考：
https://www.cnblogs.com/zghaobac/p/3999253.html
https://www.jianshu.com/p/2e6eb7386cd3