算法 & 并查集（Union-find算法）
本篇文章主要介绍并查集算法
并查集（Union-find算法）
-
- 一、动态连通性
- 二，解决问题（并查集）
- 三、quick-find 方法
- 四、quick-union方法
- 五、加权quick-union方法
- 六、总结
一、动态连通性
在介绍该算法之前，先说说从什么它是解决什么问题。
首先看图，了解动态连通性。
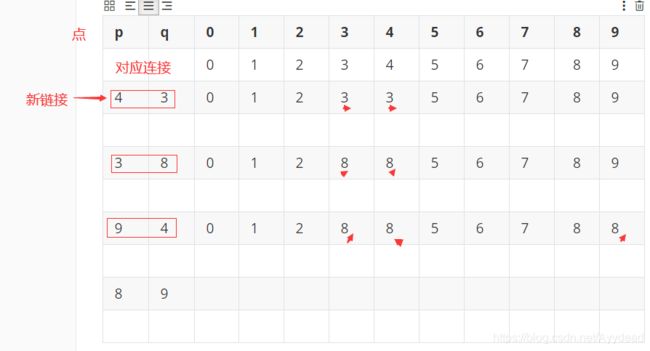
图中有10个点，每次给予一个点数对，例如（4，3），这代表着点3和点4链接在一起。是连通的。
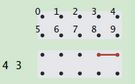
接下来，又是一个点数对（3, 8）。则3与8连上了。同样，此时隐藏着一个条件点4和点8也联系在一起了。（当然图中并没有画出来，只画出单位长度的连接）
此时，我们可以总结如下性质：
- 自反性：p 和 p 是相连的
- 对称性：如果 p和 q是相连的，那么 q和 p 也是相连的。
- 传递性：如果 p 和 q 是相连的，并且q 和 r 也是相连的，那么p 和 r也是相连的。
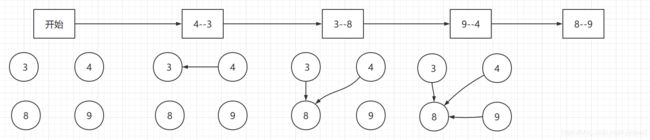
接下，（6, 5）正常操作。而（9， 4）时，当9 和 4链接上之后,由于4和8 相连，所以， 8 和 9 相连了。且是单位长度的。可以画出。如图所示
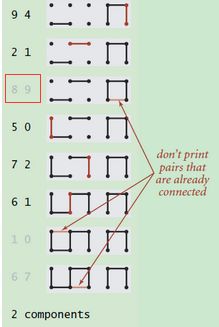
当再次出现（8， 9）连接操作时，已连接的点数集合中，就会显示 点8 和点9已经连接了。
当数目增大时，就会出现更加复杂和混乱的情况，所以如图
在此类问题中，我们就能遇到类似网络，和迷宫的实际需要解决的问题。而对于动态连通性想必就有自己的理解了。
二，解决问题（并查集）
百度定义：
并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。
并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。
其实简单想法就是，将连通的节点，一一添加到一个集合中去。如果出现 动态连通的两点，该集合也是会变化的。而这个集合可以作为查找两个点连接的数据基础。所以每次针对一个新的点连接，就会这样操作：
先去集合里查找是否存在该链接，如果有，不增加；如果没有，则增加该链接，且可能形成新的链接。
依据上述思路，简单想法就是通过数组来对应其点和点对应情况。
- 成员：存储已连接的点的集合。
- 方法：查找某个点的连接情况；判断两个点是否链接；实现新的链接点增加到集合中去；…
public abstract class UnionFind {
protected int[] id;
protected int count;//所有点的数量
public UnionFind(int N) {
//初始化分量id数组
this.count = N;
this.id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
//查找该点的链接情况
public abstract int find(int p);
//合并新的链接情况
public abstract void union(int p, int q);
public int getCount() {
return count;
}
//判断两点是否链接
public boolean connected(int p, int q) {
return find(p) == find(q);
}
}
其中我们注意到，一个点可以和多个点链接，形成对应关系。那么用数组如何表示这层关系？而且查找只是简单的查找吗？
再结合上述的 并和查两种操作，我们对这目的有不同的实现方式。
三、quick-find 方法
对，这里主要偏向去快速查找。
public class Quick_find extends UnionFind {
public Quick_find(int N) {
super(N);
}
@Override
public int find(int p) {
return id[p];
}
@Override
public void union(int p, int q) {
int pID = find(p);//点p链接的点
int qID = find(q);//点q链接的点
if (pID == qID) {
return;//即并查集中已显示此两点连接了
}
//id[p] != id[q]，此时数组中，所有和id[p]相等的元素的值均改为id[q]的值。
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
count--;
}
}
这里查找特别方便，就是直接获取数组值，但是此时归并链接对象就很麻烦了。
（4， 3） （3， 8） （9 ， 4）
这时候，3,4，9都指向了8，就会造成之后中无法直接找到3，4， 9除8之外的连接点。例如，3和4相连的，但是在集合中不能直接显示。
所以，quick-find方法，其中find方法是O（1）时间，但是union方法确实需要遍历数组，修改值，O(n)时间。
并且，点数越多，union方法，时间复杂度越高。所以，此类方法，不适合大型连通性问题。
四、quick-union方法
和上面方法不同的是，quick-union更加偏向于增加新的连接点数对。
虽然仍然用数组存储对应连接关系，但是形成一个树的结构。
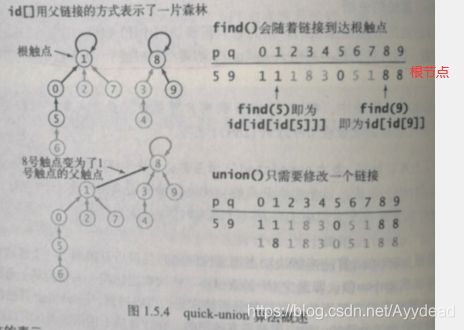这次数组存储的是每个点连接的点，同时在逻辑上形成的树中，作为该点的根节点。
这种方式的好处是： 每次增加新的连接情况时，只用修改一个点的值。所以时quick-union
但是，查找每个点的连接根节点时，自然增加查找负担。区别于quick-find
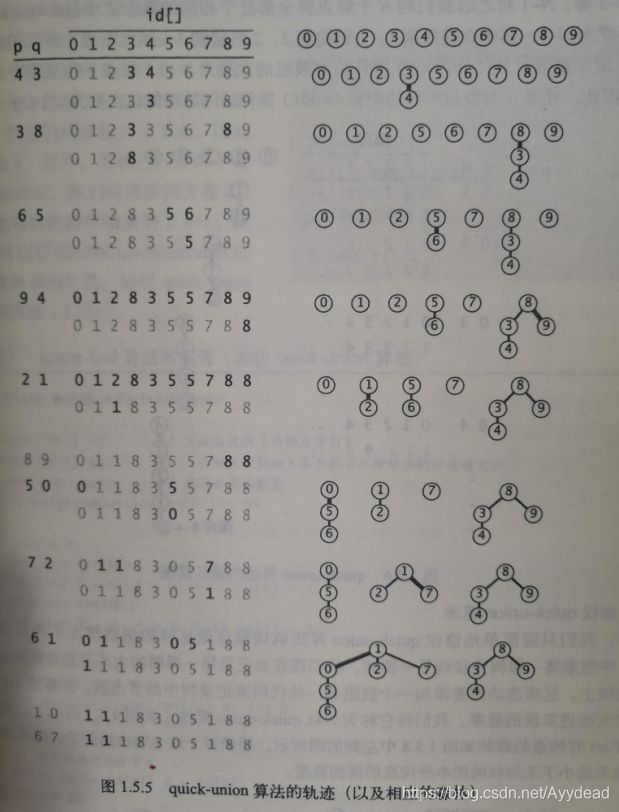
代码实现：
public class Quick_union extends UnionFind {
public Quick_union(int N) {
super(N);
}
@Override
public int find(int p) {
//寻找p节点所在组的根节点，根节点具有性质id[root] = root
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
//两个点的根节点都是一样，则代表同处一棵树，这两点相连
return;
}
id[pRoot] = qRoot; // 将一颗树(即一个组)变成另外一课树(即一个组)的子树
count--;
}
}
这时，问题来了。在面对大型数据连通问题时，quick-find 一定比quick-union慢吗？
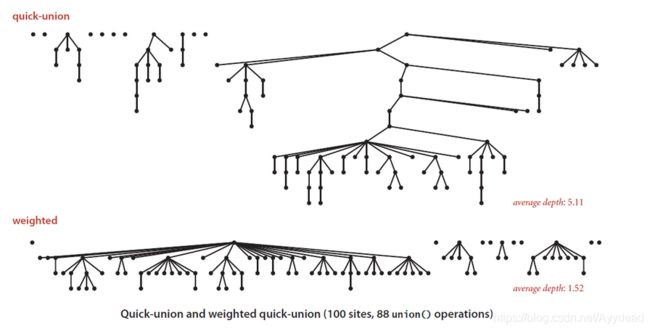
不一定。因为，如果出现一些极端情况是，由于树的深度特别深，find方法为O(n)。如图
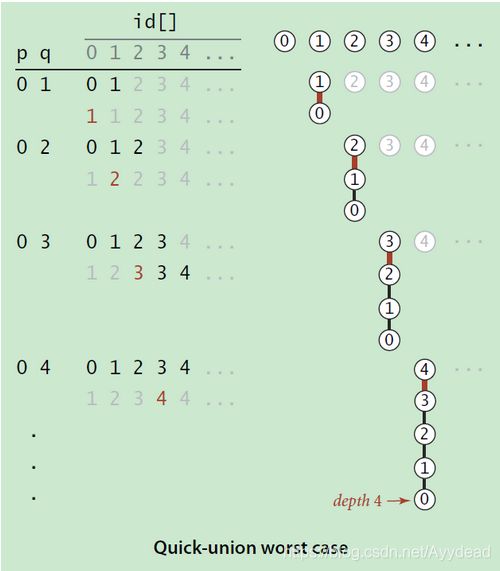
上述情况时，虽然很极端，但是确实代表着树的深度决定着find方法的时间复杂度。那么有没有解决方法？
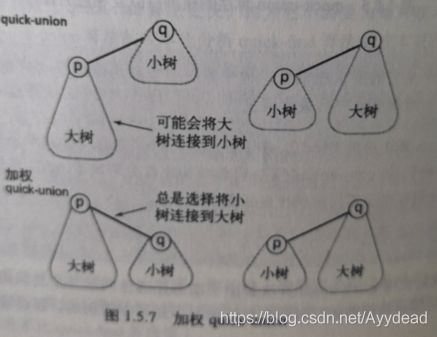
答案很容易想到，就是限制树的高度。
五、加权quick-union方法
如图，我们解决的就是两个树合并在一起的情况。
代码如下：
public class WeightQuick_union {
private int[] id;
private int[] sz;//各个根节点的树高度
private int count;
public WeightQuick_union(int N) {
this.count = N;
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
sz = new int[N];
for (int i = 0; i < N; i++) {
sz[i] = 1;//刚开始，每个树高度都为1
}
}
public int getCount() {
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int find(int p) {
while(p != id[p]) {
p = id[p];
}
return p;
}
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
//比较两个数的高度，将小树加到大树上，并且修改树高
if (sz[pRoot] < sz[qRoot]) {
id[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
}else {
id[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
count--;
}
}
下图是加权与不加权quick-union中树高度对比
六、总结
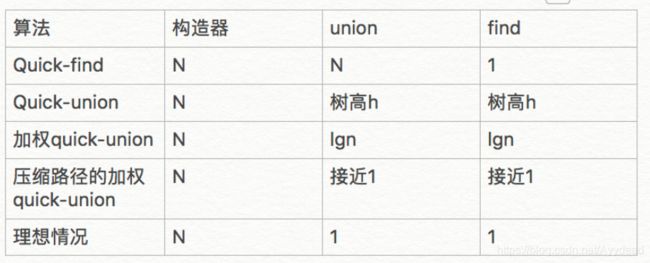关于并查集的算法是Algorithms书上学习到的例子。
优秀指导文章：并查集(Union-Find)算法介绍
有关并查集实际问题文章：用并查集(find-union)实现迷宫算法以及最短路径求解
笔者水平有限，目前只能描述以上问题，如果有其他情况，可以留言，有错误，请指教，有继续优化的，请分享，谢谢！
本篇文章是否有所收获？阅读是否舒服？又什么改进建议？希望可以给我留言或私信，您的的分享，就是我的进步。谢谢。
2020.9.8 网安院2楼