字符串匹配的Boyer-Moore算法

公司内部培训我想讲一讲grep命令的使用，正好网上有一篇文章说GNU grep命令内部字符串匹配算法用的是Boyer-Moore算法，此算法比KMP算法快3到5倍.好，那我们看看Boyer-Moore算法是如何匹配字符串的。

Boyer-Moore算法

在用于查找子字符串的算法当中，BM（Boyer-Moore）算法是目前被认为最高效的字符串搜索算法，它由Bob Boyer和J Strother Moore设计于1977年。

一般情况下，比KMP算法快3-5倍。该算法常用于文本编辑器中的搜索匹配功能，比如大家所熟知的GNU grep命令使用的就是该算法，这也是GNU grep比BSD grep快的一个重要原因。

主要特征

假设文本串text长度为n，模式串pattern长度为m，BM算法的主要特征为：

• 从右往左进行比较匹配（一般的字符串搜索算法如KMP都是从从左往右进行匹配）；
• 算法分为两个阶段：预处理阶段和搜索阶段；
• 预处理阶段时间和空间复杂度都是是O(m+)，是字符集大小，一般为256；
• 搜索阶段时间复杂度是O(mn)；
• 当模式串是非周期性的，在最坏的情况下算法需要进行3n次字符比较操作；
• 算法在最好的情况下达到O(n/m)，比如在文本串b中搜索模式串ab ，只需要n/m次比较。

算法基本思想

常规的匹配算法移动模式串的时候是从左到右，而进行比较的时候也是从左到右的，基本框架是：

while（j <= strlen(text) - strlen(pattern)）{
    for (i = 0; i < strlen(pattern) && pattern[i] == text[i + j]; ++i);

    if (i == strlen(pattern)) {
        Match;
        break;
    }
    else
        ++j；
}

而BM算法在移动模式串的时候是从左到右，而进行比较的时候是从右到左的，基本框架是：

while（j <= strlen(text) - strlen(pattern)）{
    for (i = strlen(pattern); i >= 0 && pattern[i] == text[i + j]; --i);

    if (i < 0)) {
        Match;
        break;
    }
    else
        j += BM()；
}

BM算法的精华就在于BM(text, pattern),也就是BM算法当不匹配的时候一次性可以跳过不止一个字符。即它不需要对被搜索的字符串中的字符进行逐一比较，而会跳过其中某些部分。通常搜索关键字越长，算法速度越快。它的效率来自于这样的事实：对于每一次失败的匹配尝试，算法都能够使用这些信息来排除尽可能多的无法匹配的位置。即它充分利用待搜索字符串的一些特征，加快了搜索的步骤。

BM算法实际上包含两个并行的算法（也就是两个启发策略）：

坏字符算法（bad-character shift）和好后缀算法（good-suffix shift）。

这两种算法的目的就是让模式串每次向右移动尽可能大的距离（即上面的BM()尽可能大）。

一些说明

下面，就Moore教授自己的例子来解释这种算法。

假定字符串text为”HERE_IS_A_SIMPLE_EXAMPLE”，搜索词pattern为”EXAMPLE”。

HERE_IS_A_SIMPLE_EXAMPLE
EXAMPLE

首先，”字符串”与”搜索词”头部对齐，从尾部开始比较。

这是一个很聪明的想法，因为如果尾部字符不匹配，那么只要一次比较，就可以知道前7个字符（整体上）肯定不是要找的结果。

我们看到，”S”与”E”不匹配。这时，”S”就被称为”坏字符”（bad character），即不匹配的字符。

如果比较的字符串位置为如下所示：

HERE_IS_A_SIMPLE_EXAMPLE
         EXAMPLE

pattern中的”MPLE”与text完全匹配，我们把这种情况称为”好后缀”（good suffix），即所有尾部匹配的字符串。
注意，”MPLE”、”PLE”、”LE”、”E”都是好后缀。

BM算法理论探讨

坏字符算法

当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对，然后继续匹配。

坏字符算法有两种情况。

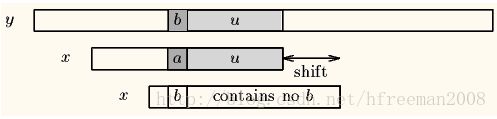
Case1：模式串中有对应的坏字符时，让模式串中最靠右的对应字符与坏字符相对（PS：BM不可能走回头路，因为若是回头路，则移动距离就是负数了，肯定不是最大移动步数了），如下图。

Case2：模式串中不存在坏字符，很好，直接右移整个模式串长度这么大步数，如下图。

好后缀算法

如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀或后缀的部分, 那把下一个后缀或部分移动到当前后缀位置。

假如说，pattern的后u个字符和text都已经匹配了，但是接下来的一个字符不匹配，我需要移动才能匹配。

如果说后u个字符在pattern其他位置也出现过或部分出现，我们将pattern右移到前面的u个字符或部分和最后的u个字符或部分相同，

如果说后u个字符在pattern其他位置完全没有出现，很好，直接右移整个pattern。

这样，好后缀算法有三种情况，如下图所示：

Case1：模式串中有子串和好后缀完全匹配，则将最靠右的那个子串移动到好后缀的位置继续进行匹配。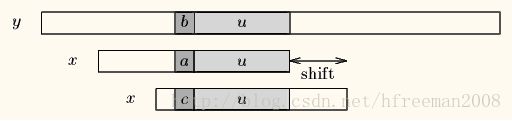

Case2：如果不存在和好后缀完全匹配的子串，则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。（此图其实非常清楚明白的说明了，如果是部分好后缀匹配的话，此匹配的好后缀一定是要在模式串的最前面，也就是头部）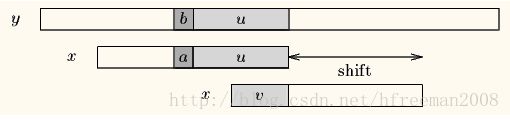

Case3：如果完全不存在和好后缀匹配的子串，则右移整个模式串。

移动规则

BM算法的移动规则是：
将3中算法基本框架中的j += BM()，换成j += MAX（shift（好后缀），shift（坏字符）），
即BM算法是每次向右移动模式串的距离是，按照好后缀算法和坏字符算法计算得到的最大值。

shift（好后缀）和shift（坏字符）通过模式串的预处理数组的简单计算得到。坏字符算法的预处理数组是bmBc[]，好后缀算法的预处理数组是bmGs[]。

BM算法应用一

我们使用BM算法来应用在Moore教授自己的例子上，来解释一下这种算法。
假定字符串
text为”HERE_IS_A_SIMPLE_EXAMPLE”，搜索词pattern为”EXAMPLE”。

HERE_IS_A_SIMPLE_EXAMPLE
EXAMPLE

从pattern的最右边开始与text比较，pattern[6]=”E”与“S”不相等时，“S”为坏字符，并且“S”在pattern中没有匹配的字符，则根据坏字符算法的第二种情况，直接整体将pattern整个移动7（strlen(pattern)）位。

HERE_IS_A_SIMPLE_EXAMPLE
       EXAMPLE

从pattern的最右边开始与text比较，pattern[6]=”E”与“P”不相等时，“P”为坏字符，并且“P”在pattern中有匹配的字符pattern[4]=”P”，则根据坏字符算法的第一种情况，直接整体将pattern整个移动2位，以后pattern中最靠右的对应字符pattern[4]=”P”与坏字符相对。

HERE_IS_A_SIMPLE_EXAMPLE
         EXAMPLE

现在，这个情况我们可以看到pattern看的后四位与text是完全匹配的，也就是说“MPLE”是好后缀，pattern[2]=”A”与text中的“I”是不匹配的，也就是说“I”是坏字符。

根据坏字符算法，此情况属于坏字符算法中的第二种情况，我们直接将pattern移动3位：

HERE_IS_A_SIMPLE_EXAMPLE
            EXAMPLE

我们再根据好后缀算法，此情况属于好后缀算法中的第二种情况，其中pattern[0]=”E”与好后缀（“MPLE”，“PLE”，“LE”，“E”）中的”E”匹配，我们直接将pattern移动6位，使得pattern[0]=”E”与text中的“E”匹配：

HERE_IS_A_SIMPLE_EXAMPLE
               EXAMPLE

说明：

如果”好后缀”有多个，则除了最长的那个”好后缀”，其他”好后缀”的上一次出现位置必须在头部。

比如，假定”BABCDAB”的”好后缀”是”DAB”、”AB”、”B”，请问这时”好后缀”的上一次出现位置是什么？

回答是，此时采用的好后缀是”B”，它的上一次出现位置是头部，即第0位。
这个规则也可以这样表达：如果最长的那个”好后缀”只出现一次，则可以把搜索词改写成如下形式进行位置计算”(DA)BABCDAB”，即虚拟加入最前面的”DA”。

所以，此时，综合坏字符算法（移动2位）与好后缀算法（移动6位），BM算法为选择其中最大的值，故我们选择好后缀算法移动6位，如下图：

HERE_IS_A_SIMPLE_EXAMPLE
               EXAMPLE

此时pattern[6]=”E”与“P”比较不匹配，则“P”为坏字符，坏字符”P”与patter[4]=”P”匹配,根据坏字符算法的第二种情况，我们移动2位：

HERE_IS_A_SIMPLE_EXAMPLE
                 EXAMPLE

尾部开始逐位比较，发现全部匹配，于是搜索结束。如果还要继续查找（即找出全部匹配），则根据”好后缀规则”，后移 6位，即头部的”E”移到尾部的”E”的位置。

BM算法具体执行

BM算法子串比较失配时，按坏字符算法计算pattern需要右移的距离，要借助bmBc数组，而按好后缀算法计算pattern右移的距离则要借助bmGs数组。下面讲下怎么计算bmBc[]和bmGs[]这两个预处理数组。

计算坏字符数组bmBc[]

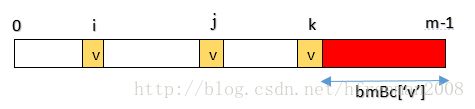
这个计算应该很容易，似乎只需要bmBc[i] = m - 1 - i就行了，但这样是不对的，因为i位置处的字符可能在pattern中多处出现（如下图所示），而我们需要的是最右边的位置，这样就需要每次循环判断了，非常麻烦，性能差。

这里有个小技巧，就是使用字符作为下标而不是位置数字作为下标。这样只需要遍历一遍即可，这貌似是空间换时间的做法，但如果是纯8位字符也只需要256个空间大小，而且对于大模式，可能本身长度就超过了256，所以这样做是值得的（这也是为什么数据越大，BM算法越高效的原因之一）。

如前所述，bmBc[]的计算分两种情况，与前一一对应。
Case1：字符在模式串中有出现，bmBc[‘v’]表示字符v在模式串中最后一次出现的位置，距离模式串串尾的长度，如上图所示。

Case2：字符在模式串中没有出现，如模式串中没有字符v，则BmBc[‘v’] = strlen(pattern)。

写成代码也非常简单：

void PreBmBc(char *pattern, int m, int bmBc[])
{
    int i;

    for(i = 0; i < 256; i++)
    {
        bmBc[i] = m;
    }

    for(i = 0; i < m - 1; i++)
    {
        bmBc[pattern[i]] = m - 1 - i;
    }
}

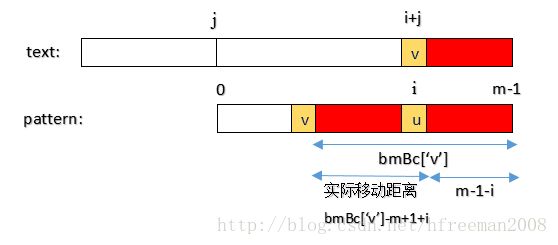
计算pattern需要右移的距离，要借助bmBc数组，那么bmBc的值是不是就是pattern实际要右移的距离呢？No，想想也不是，比如前面举例说到利用bmBc算法还可能走回头路，也就是右移的距离是负数，而bmBc的值绝对不可能是负数，所以两者不相等。那么pattern实际右移的距离怎么算呢？这个就要看text中坏字符的位置了，前面说过坏字符算法是针对text的，还是看图吧，一目了然。

图中v是text中的坏字符（对应位置i+j）,在pattern中对应不匹配的位置为i，那么pattern实际要右移的距离就是：bmBc[‘v’] - m + 1 + i。

计算好后缀数组bmGs[]

这里bmGs[]的下标是数字而不是字符了，表示字符在pattern中位置。
如前所述，bmGs数组的计算分三种情况，与前一一对应。假设图中好后缀长度用数组suff[]表示。

Case1：对应好后缀算法case1，如下图，j是好后缀之前的那个位置。

Case2：对应好后缀算法case2：如下图所示：

Case3：对应与好后缀算法case3，bmGs[i] = strlen（pattern）= m

这样就清晰了，代码编写也比较简单：

void PreBmGs(char *pattern, int m, int bmGs[])
{
    int i, j;
    int suff[SIZE]; 

    // 计算后缀数组
    suffix(pattern, m, suff);

    // 先全部赋值为m，包含Case3
    for(i = 0; i < m; i++)
    {
        bmGs[i] = m;
    }

    // Case2
    j = 0;
    for(i = m - 1; i >= 0; i--)
    {
        if(suff[i] == i + 1)
        {
            for(; j < m - 1 - i; j++)
            {
                if(bmGs[j] == m)
                    bmGs[j] = m - 1 - i;
            }
        }
    }

    // Case1
    for(i = 0; i <= m - 2; i++)
    {
        bmGs[m - 1 - suff[i]] = m - 1 - i;
    }
}

o easy? 结束了吗？还差一步呢，这里的suff[]咋求呢？

在计算bmGc数组时，为提高效率，先计算辅助数组suff[]表示好后缀的长度。

suff数组的定义：m是pattern的长度

a. suffix[m-1] = m;
b. suffix[i] = k
for [ pattern[i-k+1] ….,pattern[i]] == [pattern[m-1-k+1]，pattern[m-1]]
看上去有些晦涩难懂，实际上suff[i]就是求pattern中以i位置字符为后缀和以最后一个字符为后缀的公共后缀串的长度。不知道这样说清楚了没有，还是举个例子吧：

i   : 0 1 2 3 4 5 6 7  

pattern: b c a b a b a b

当i=7时，按定义suff[7] = strlen(pattern) = 8
当i=6时，以pattern[6]为后缀的后缀串为bcababa，以最后一个字符b为后缀的后缀串为bcababab，两者没有公共后缀串，所以suff[6] = 0
当i=5时，以pattern[5]为后缀的后缀串为bcabab，以最后一个字符b为后缀的后缀串为bcababab，两者的公共后缀串为abab，所以suff[5] = 4
以此类推……
当i=0时，以pattern[0]为后缀的后缀串为b，以最后一个字符b为后缀的后缀串为bcababab，两者的公共后缀串为b，所以suff[0] = 1

这样看来代码也很好写：

void suffix(char *pattern, int m, int suff[])
{
    int i, j;
    int k;

    suff[m - 1] = m;

    for(i = m - 2; i >= 0; i--)
    {
        j = i;
        while(j >= 0 && pattern[j] == pattern[m - 1 - i + j]) j--;

        suff[i] = i - j;
    }
}

参考资料

1.字符串匹配的Boyer-Moore算法
http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
2.grep之字符串搜索算法Boyer-Moore由浅入深（比KMP快3-5倍）
http://blog.jobbole.com/52830/
3.字符串搜索算法Boyer-Moore的Java实现
http://blog.csdn.net/nmgrd/article/details/51697567
4.Boyer-Moore算法学习
http://blog.csdn.net/sealyao/article/details/4568167
5.grep之字符串搜索算法Boyer-Moore由浅入深（比KMP快3-5倍）
http://www.cnblogs.com/lemon66/p/4858890.html