【程序员必修数学课】->基础思想篇->迭代法

Ⅰ 象棋&米粒-迭代法

这里引用一个大家从小就听过的小故事。

传说，印度的舍罕国王打算重赏国际象棋的发明人——大臣西萨·班·达依尔。这位聪明的大臣跪在国王面敢说：“陛下，请你在这张棋盘的第一个小格内，赏给我一粒麦子，在第二个小格内给两粒，在第三个小格内给四粒，照这样下去，每一小格内都比前一小格加一倍。陛下啊，把这样摆满棋盘上所有64格的麦粒，都赏给您的仆人吧?”国王说：“你的要求不高，会如愿以偿的”。说着，他下令把一袋麦子拿到宝座前，计算麦粒的工作开始了。……还没到第二十小格，袋子已经空了，一袋又一袋的麦子被扛到国王面前来。但是，麦粒数一格接一格地增长得那样迅速，很快看出，即使拿出来全印度的粮食，国王也兑现不了他对象棋发明人许下的语言。

这个故事中的计算麦粒的方法，在数学上是有对应方法的，这也正是这篇文章要讲的概念——迭代法（Iterative Method）。

那么到底什么是迭代法呢？

简单来说，迭代法就是不断地用旧的变量值，递推计算新的变量值。

我们回到这个国际象棋的故事，大臣要求每一格的麦子都是前一格的两倍，那么前一格里麦子的数量就是旧的变量值，我们可以先记作 X_n-1 ；而当前格子里麦子的数量就是新的变量值，我们记作 X_n 。这两个变量的递推关系如下

有编程经验的人很容易就想到，迭代的思想可以通过计算机语言中的循环语句来实现。计算机本身就很适合做重复性的工作，我们可以通过循环语句，让计算机重复执行迭代中的递推步骤，然后推导出变量的最终值。

Ⅱ 编程求麦粒的数量

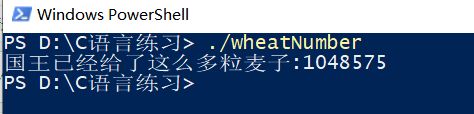
这里我用C语言实现一下这个迭代过程。

#include 

long getNumberOfWheat(int grid);

long getNumberOfWheat(int grid) {
     
	int i = 2;
	long sum = 0;                 //麦子的总数
	long numberOfWheatInGrid = 0; //当前格子上麦子的数量

	numberOfWheatInGrid = 1;
	sum += numberOfWheatInGrid;

	for (; i <= grid; i++) {
     
		numberOfWheatInGrid *= 2;
		sum += numberOfWheatInGrid;
	}
	return sum;
}

int main() {
     
	int grid;
	long sum;

	grid = 20;

	sum = getNumberOfWheat(grid);

	printf("国王已经给了这么多粒麦子:%ld", sum);

	return 0;
}

我用第20格作为测试，迭代到后面会超出C语言数据结构能表示的最大值了。

测试结果如下

Ⅲ 迭代法的应用

大体上，迭代法可以运用在以下几个方面：

• 求数值的精确或者近似解。 典型的方法包括 二分法（Bisection method）和 牛顿迭代法（Newton`s method）。
• 在一定范围内查找目标值。 典型的方法包括 二分查找。
• 机器学习算法中的迭代。 相关的算法或者模型很多，比如 K-均值算法（K-means clustering）、PageRank 的马尔科夫链（Markov chain）、梯度下降法（Gradient descent）等等。迭代法之所以在机器学习中有广泛的应用，是因为很多时候机器学习的过程，就是根据已知的数据和一定的假设，求一个局部最优解。 而迭代法可以帮助学习算法逐步搜索，直至发现这种解。

在这里我主要说一下求数值的解和查找匹配记录这两个应用。

① 求方程的精确或者近似解

迭代法在数学和编程中的应用有很多，如果只能用来计算庞大的数字，那就太暴殄天物了。
迭代还可以帮助我们进行无穷地逼近，求得方程的精确或者近似解。

比如说，我们想计算某个给定正整数 n（n > 1）的平方根，如果不用编程语言自带的函数，要怎么做呢？

假设有正整数 n ，这个平方根一定小于 n 本身，并且大于 1。那么这个问题就转化成了，在 1 到 n 之间，找一个数字等于 n 的平方根。

这里我采用迭代中常见的二分法。每次查看区间内的中间值，检验它是否符合标准。

举个例子，假如我们要找到 10 的平方根。我们需要先看 1 到 10 的中间数值，也就是（1 + 10）/ 2 = 5.5 。 5.5 的平方是大于 10 的，所以我们需要一个更小的数值，就看 5.5 和 1 之间的 3.25 。由于 3.25 的平方也是大于 10 的，继续查看 3.25 和 1 之间的数值，也就是 2.125 。这时，2.125 的平方小于 10 了，所以看 2.125 和 3.25 之间的值，一直继续下去，直到发现某个数的平方正好是 10 。

同样的，我用C语言来简单实现一下这个功能。

#include 
#include 

double getSqureRoot(int number, int maxTry, double threshold);

double getSqureRoot(int number, int maxTry, double threshold) {
     
	int i;
	double middle;
	double squre;
	double delta;
	double min = 1.0;
	double max = (double) number;

	if (number <= 1) {
     
		return -1.0;
	}
	for (i = 0; i < maxTry; i++) {
     
		middle = (max - min) / 2 + min;
		squre = middle * middle;
		delta = fabs(squre / number - 1);

		if (delta <= threshold) {
     
			return middle;
		} else {
     
			if (squre > number) {
     
				max = middle;
			} else {
     
				min = middle;
			}
		}
	}
	return -2.0;
}

int main() {
     
	int number = 10;
	double squreRoot = getSqureRoot(number, 10000, 0.000001);

	if (-1.0 == squreRoot) {
     
		printf("输入的数小于1.\n");
	} else if (-2.0 == squreRoot) {
     
		printf("未能找到解.\n");
	} else {
     
		printf("该数的解为:%lf\n", squreRoot);
	}

	return 0;
}

这里我说几个细节。

middle = (max - min) / 2 + min

这里我用的是这个式子而不是(max + min) / 2，是因为如果max和min都已经接近数据的极限，两个数相加就会溢出，所以替换成了先减，然后用两个数的差的二分之一再加，这样就不会溢出了。两个式子化简下来其实是一样的。

int maxTry是最多尝试的次数，防止程序耗时太久。double threshold是精度，也是一个保护机制，如果找不到精确解，误差小于规定的精度也可以退出循环。

delta = fabs(squre / number - 1);

这个就是算的误差占原值的百分比，来控制迭代的结束。

这就是二分迭代法。这里我简单地提一下牛顿迭代法。

牛顿迭代法是牛顿在17世纪提出的一种方法，用于求方程的近似解。这种方法以微分为基础，每次迭代的时候，它都会去找到比上一个值 x₀ 更接近的方程的根，最终找到近似解。该方法及其延伸也被应用在机器学习的算法中，在我后面的文章中，我会详细讲解。

② 查找匹配记录

二分法中的迭代式逼近，不仅可以帮我们求得近似解，还可以帮助我们查找匹配的记录。这里我举一个查通讯录的例子。

比如你有一本通讯录，按照名字的首字母从A到Z排列。

如果你要查找一个名字，自然要从中间开始，如果中间的字母在要找的名字的前面，那就可以不用管前半边了，直接从后半部分再取中间，然后看字母的顺序。就这样持续地迭代式查找，直到范围缩小到单个的名字。如果最终仍然无法找到，则返回不存在。

这个方法的整体思路和二分法求解平方根是一致的，主要区别在两个方面：
第一，每次判断是否终结迭代的条件不同。求平方根的时候我们需要判断某个数的平方是否和输入的数据一致。而这里，我们需要判断通讯录中某个单词是否和待查的单词相同；
第二，二分查找需要确保被搜索的空间是有序的。

这里我就不写代码了，因为道理都是一样的。

关于迭代法的内容就完了，日常的编程中我们要多观察问题的现象，思考其本质，看看不断更新变量值或者缩小搜索的区间范围，是否可以获得最终的解（或近似解、局部最优解），如果是，那就可以尝试迭代法。

另，这篇文章的知识点来源于极客时间黄申的《程序员的数学基础课》。