巨大数运算

巨大数运算

在int是四字节补码的前提下，很容易得出int类型的变量所能表示的最大正数是21亿多，如果我们要处理的数据远远大于21亿，那么该怎么办呢？并且如果我们的数据超出极限，那么便会产生错误。下面代码便是证明

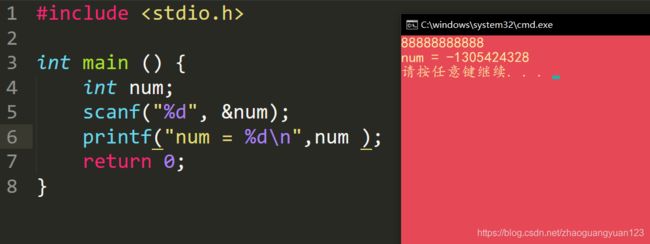
可以看到当输入为800多亿的时候，已经产生了错误的输出结果。为了解决这个问题，我们来编写一个程序，来完成对任意大小的数据加减乘除运算，并且为了简便，在此只讨论整数的情况

核心技术 1

万进制存储

对于这个问题，最最直白又直接的处理方案就是把数据存储在字符数组中，并且逐位计算，处理每一位时还要根据ASCII码进行转换，并且还要涉及很多的进位和借位问题。显然，在面对庞大的数据量时，这种方法效率非常低下。

为此，引入万进制存储方案。

万进制顾名思义，便是逢万进一，将数据的每四位作为一个存储单位存入int类型的数组中，在未来面对的计算中，参与计算的最小单位便是4位。万进制在理解上与十进制，二进制，八进制，十六进制并没有什么本质不同，并且他们的基本原理都是相似的。但是为什么要采用万进制呢 ？

首先，就效率而言，万进制每次处理四位，显然比上文中提到的第一种方案要高效很多。但可能有人会问为什么不是十万进制，这效率不是更高吗。
再进行乘法时，对于两个单位的相乘最大表示9999 * 9999 = 99980001 ，
而 99980001是在4字节补码范围之内的，但是当十万进制时，便会产生
99999 * 99999 = 9999800001 > 21亿 便会产生错误，因此采用万进制既可以保证一定的效率同时又能保证存储的数据的有效性。

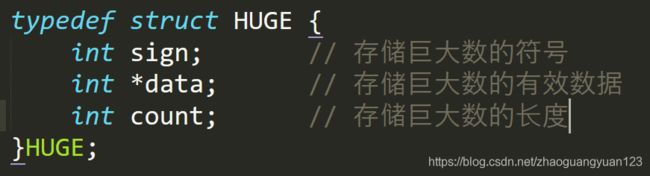
对于万进制的处理，可以用一个结构体来控制

巨大数结构体

三个结构体成员便把巨大数的基本信息处理完成。

我们在此默认巨大数最开始是存储在文件中的，以后所有数据的提取和写入都是基于文件操作。在此前提下，我们继续进行后面的操作

首先考虑两种非常普遍但对于编程不友好的加减情况

Case 1

加法运算

被加数 -999 加数 10000

---

，虽然规定是加法，但是按照我们小学二年级就学过的加减运算法则， 我们的大脑会先观察到后面的数字10000大于999， 所以其实我们手工计算过程是计算10000 - 999 ，显而易见，这是个减法。

Case 2

减法运算

被减数 -999 减数-10000

同样在这种情况下，-999 -（-10000），小学二年级的我们就知道我们其实是在计算10000-999，但是让计算机懂得完成-999 -（-10000）—>10000 - 999 是挺麻烦的。

当然我们更希望看到的是诸如999 + 10000 的情况。
所以我们需要一种能合并加减法的处理方案

考虑计算机中为什么要有补码？

首先考虑反码

反码的出现，主要是为了解决原码无法执行减法运算的问题，人为规定反码最高位为符号位，正数为0，负数为1，反码正数与原码正数格式一致，反码负数为负数绝对值的原码按位分别取反。

但是显然按这种方式0会有两种编码。为此又产生补码。正数的补码与原码格式相同，负数的补码是将负数绝对值的原码分别按位取反，并加1。
至此，解决了计算机将减法转换成加法的问题。

基于以上的思考和讨论，下面引出一种新颖的处理方式

核心技术2

微易码补码

首先声明，此种处理方案并非个人原创，而是由教主提出并且传授。

微易码补码的思想，类似于计算机中的补码和反码，其根本出发点是为了统一加减运算。下面我将详细阐述此种思想。

对于两个参与运算的数据A与B， 假设A的位数为X，B的位数为Y，那么设
X = max{（X + 3）/ 4 + 1，（Y+ 3）/ 4 + 1},要求数据A和B都要扩充至X位，下面讲述扩充原则
对于正数，每四位一组， 不够位数便补0，直到补齐X位，对于负数，每四位一组，并且每一位都需要用9999减去本位原始s数值，不够位数补9999，直到补齐X位，，为了更形象，给出几个列子帮助读者理解。

省略号前面还有多少位完全取决于X = max{（X + 3）/ 4 + 1，（Y+ 3）/ 4 + 1}这个式子。下面阐述计算原则。

对于计算规则，按照转换为微易码补码之后的形式，每四位一组相加，逢万进一，对于A最前面的一位，B最前的一位，为0记为0，为9999记为1，
二者按位相与，若最后一位进位了，记为1，并且整个数据最后一位加一，没有进位记为0，用0或者1与前面按位相与的结果继续按位相与，若最后得到0，说明结果为正数，若为1，则结果为负数，并且结果需要每位都用9999减去本位数值，即可得到最后结果。

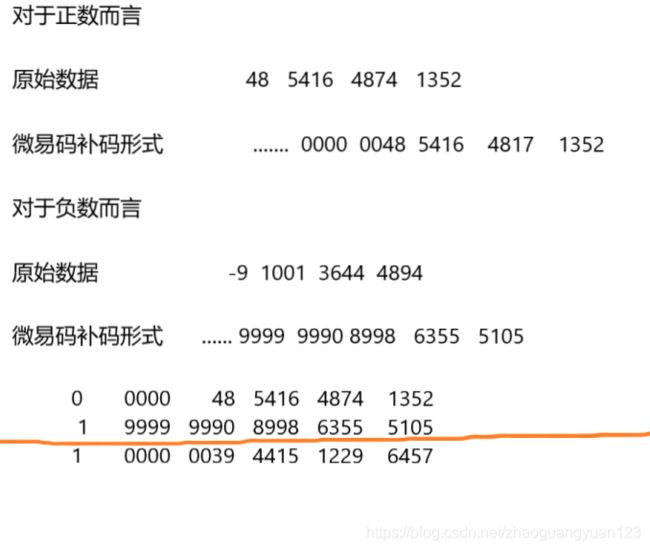
上图中0， 1 ，1三个数从前向后依次按位相与得到0，说明结果为正数，首位变为了0000说明首位进位了，那么末尾6457 + 1 = 6458.
以上便是对微易码补码运算的一些规则和手工过程说明

下面从代码角度阐述如何实现

代码实现

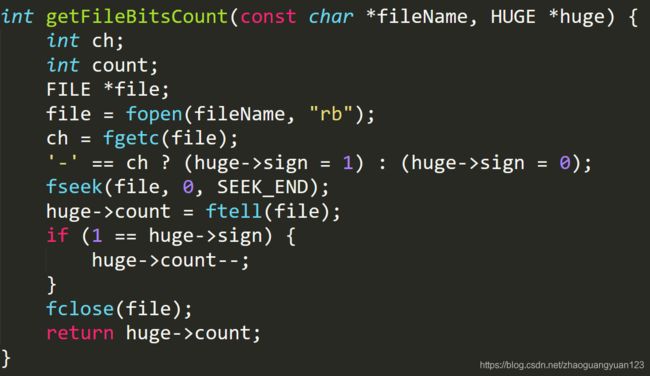
首先需要一个函数来得到文件中巨大数的位数
通过此函数给huge->count赋值并且该函数返回巨大数位数

int initArray(const char *fileNameOne, const char *fileNameAnother, HUGE *hugeOne, HUGE *hugeAnother) {
     
	int fileSizeOne;
	int fileSizeAnother;
	int fileSizeMax;
	fileSizeOne = (getFileBitsCount(fileNameOne, hugeOne) + 3) / 4 + 1;
	fileSizeAnother = (getFileBitsCount(fileNameAnother, hugeAnother) + 3) / 4 + 1;
	fileSizeMax =  fileSizeOne > fileSizeAnother ? fileSizeOne : fileSizeAnother;
	hugeOne->data = (int *) calloc(sizeof(int), fileSizeMax);
	hugeAnother->data = (int *) calloc(sizeof(int), fileSizeMax);
	return fileSizeMax;

}

此函数可以实现对巨大数存储数组空间的申请，完成对巨大数的初始化。

下面便要进行将文件中的数据每四位一组逐组存入huge->data[index]中

void inputDataToArray(const char *fileName, HUGE *huge) {
     
	FILE *file;
	int ch;
	int index;
	int i;
	int sum = 0;
	int bits = huge->count;
	int fileSize = (huge->count + 3) / 4;
	file = fopen(fileName, "rb");
	1 == huge->sign ? fseek(file, 1, SEEK_SET) : fseek(file, 0, SEEK_SET);
	for (index = 0; index < fileSize; index++) {
     
		for (i = 0; i < (0 == bits % 4 ? 4 : bits % 4); i++) {
     
			ch = fgetc(file);
			sum = 10 * sum + ch - '0';
		}
		huge->data[fileSize-1-index] = sum;
		sum = 0;
		bits -= i;
	}
	if (1 == huge->sign) {
     
		for (index = 0; index < fileSize; index++) {
     
			huge->data[index] = 9999 - huge->data[index];
		}
	}
}

因位按照微易码补码的格式要求，我们还需要将数组中现有的数据改变格式，使其符合微易码补码的格式要求以便进行计算，为此，利用以下函数完成

void unifyFormat(HUGE *hugeOne, HUGE *hugeAnother, const int fileSizeMax) {
     
	int index;
	int fileSizeOne = (hugeOne->count + 3) / 4;
	int fileSizeAnother = (hugeAnother->count + 3) / 4;

	for (index = fileSizeOne; index < fileSizeMax; index++) {
     
		hugeOne->data[index] = (hugeOne->sign == 1 ? 9999 : 0);
	}
	for (index = fileSizeAnother; index < fileSizeMax; index++) {
     
		hugeAnother->data[index] = (hugeAnother->sign == 1 ? 9999 : 0);
	}
}

现在便可以真正意义上的计算了。计算由下面函数完成

void calculateArray(HUGE *hugeOne, HUGE *hugeAnother, const int fileSizeMax, const char *resFileName) {
     
	int index = 0;
	int sum;
	int bit = 0;
	int i = 0;
	int *resArray;
	int Sign;
	resArray = (int *) calloc(sizeof(int), fileSizeMax);
	while (index < fileSizeMax) {
     
		// 计算
		sum = hugeOne->data[index] + hugeAnother->data[index] + bit;
		sum >= 10000 ? (bit = 1) : (bit = 0);
		sum >= 10000 ? (sum -= 10000) : (sum = sum);
		resArray[index++] = sum;
	}
	
	if (1 == bit) {
       // 处理正负号以及补码问题
		++resArray[0];
	}
	if (1 == (Sign = (hugeOne->sign ^ hugeAnother->sign) ^ bit)) {
     
		for (index = 0; index < fileSizeMax; index++) {
     
			resArray[index] = 9999 - resArray[index];
		}
		inputDataToResFile(resArray, Sign, fileSizeMax, resFileName);
		return;
	}	
	inputDataToResFile(resArray, Sign, fileSizeMax, resFileName);
}

另外**inputDataToResFile()**函数还要注意处理对向文件出入数据的格式细节问题，如若首位为0，应该不进行输入，首位不足1000不应该补0，后面的位数应该按照 **fprintf(resFile, “%04d”,res[fileSizeMax - 1 - index]);**的格式输入文件。具体细节不在讨论。

下面为加法代码

void AddingBigNumber(const char *fileNameOne, const char *fileNameAnother, const char *resFileName, HUGE *hugeOne, HUGE *hugeAnother) {
     
	int fileSizeMax;
	fileSizeMax = initArray(fileNameOne, fileNameAnother, hugeOne, hugeAnother);
	inputDataToArray(fileNameOne, hugeOne);
	inputDataToArray(fileNameAnother, hugeAnother);
	unifyFormat(hugeOne, hugeAnother, fileSizeMax);
	calculateArray(hugeOne, hugeAnother, fileSizeMax, resFileName);
}

关于减法运算，只需要将后一个文件中的数据的huge->sign改变一下便可以转换成为加法，在加法完成的情况下非常简单。

对于乘法，可以完全按照手工算式过程进行，并且乘法中还是需要不断调用加法运算，因此在加法完成的基础上也可以轻松实现。

鉴于本人能力有限，目前对于除法没有非常高效又简洁的方案，在此暂时无法讨论。

总结

整个项目的核心技术便是微易码补码，也正是因为微易码补码的引入，大大简化了程序，提高了效率，而掌握微易码补码的手工过程是完成代码的关键。
本篇博文写于本人大一暑假，因个人能力有限，文中可能有些许错误和表达不当的地方，还请大家指正。