小红书秋招笔试题
后端题编程题:
import java.util.Scanner;
/**
* 输入:10 [2,3,5]
* 输出:4
*/
public class Main {
static int count = 0; //全局变量。用于统计组合的个数
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
/* 每一个测试用例清零。(注意:一定要有这一行!) */
count = 0;
String[] str = sc.nextLine().split(" "); //切分为"10" 和 "[2,3,5]"
/* 薯券金额 */
int money = Integer.parseInt(str[0]);
/* 从"[2,3,5]"中,取出商品价格,然后存放到prices数组中。 */
String strTmp = str[1].substring(1, str[1].length() - 1); //"2,3,5"
String[] strArray = strTmp.split(",");
int[] prices = new int[strArray.length];
for (int i = 0; i < prices.length; i++) {
prices[i] = Integer.parseInt(strArray[i]);
}
/* 输入校验 */
if (money <= 0 || prices.length <= 0) {
return;
}
/* 搜索所有可能的组合 */
depthFirstSearch(money, 0, 0, prices);
/* 输出结果 */
System.out.println(count);
}
}
/**
* @param money 总钱数
* @param curNum 当前花了多少钱
* @param curBegin 遍历prices数组的“当前起点”。每一轮递归,prices[]可选的个数就少一个,这样能避免出现重复的排列组合。
* @param prices 商品价格数组
*/
public static void depthFirstSearch(int money, int curNum, int curBegin, int[] prices) {
for (int i = curBegin; i < prices.length; i++) {
if (curNum + prices[i] == money) {
count++;
return;
} else if (curNum + prices[i] < money) {
depthFirstSearch(money, curNum + prices[i], i, prices);
} else {
return;
}
}
}
}
算法题1:
import java.util.Scanner;
//the sky is blue!
//blue! is sky the
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
String[] str = sc.nextLine().split("\\s+");
//反向构建字符串
StringBuffer sb=new StringBuffer(str[str.length-1]);
for (int i = str.length-2; i >= 0; i--) {
sb.append(" "+str[i]);;
}
System.out.println(sb.toString());
}
}
}
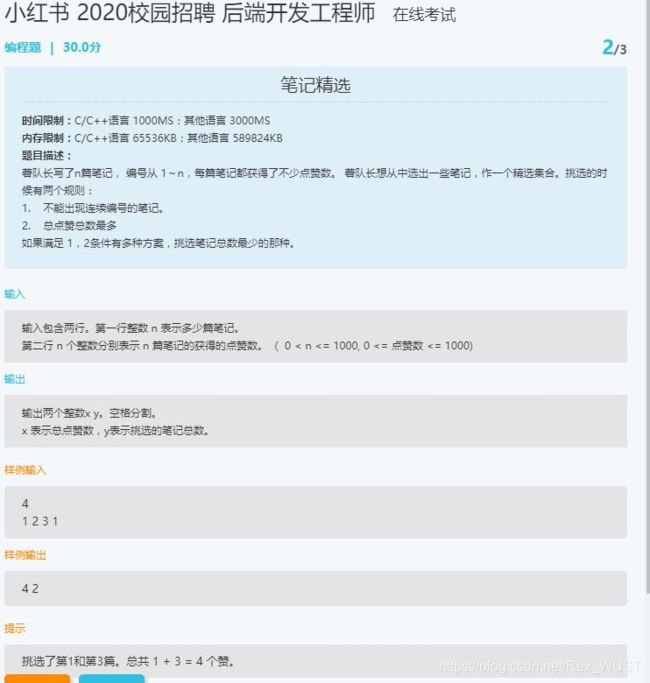
算法题2:
解法:同时更新两个dp表。第一个dp表记录总赞数。第二个dp表记录笔记数。
package b;
import java.util.Scanner;
/**
* 4
* 1 2 3 1
*
* 5
* 2 3 2 3 2
*
* 7
* 5 1 1 5 1 1 5
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int num = sc.nextInt(); //笔记数
int[] like = new int[num]; //点赞数
for (int i = 0; i < num; i++) {
like[i] = sc.nextInt();
}
if (num < 2) {
System.out.println(Math.max(like[0], like[1]) + " " + 1);
}
//根据题目给的两个规则,然后动态规划求解
int[] dp1 = new int[num]; //记录总点赞数
int[] dp2 = new int[num]; //记录挑选的笔记总数
dp1[0] = like[0];
dp1[1] = Math.max(like[0], like[1]);
dp2[0] = 1;
dp2[1] = 1;
for (int i = 2; i < num; i++) {
if (dp1[i - 2] + like[i] > dp1[i - 1]) { //注意大于的时候,才有必要更新,等于的时候,因为想要的文件最少,所以不用更新。
dp1[i] = dp1[i - 2] + like[i];
dp2[i] = dp2[i - 2] + 1;
} else {
dp1[i] = dp1[i - 1];
dp2[i] = dp2[i - 1];
}
}
int minNoteNum = dp2[num - 1];
//如果点赞数相同,返回文件个数较少的那个
for (int i = 0; i < num - 1; i++) { //顺序查找,找到的第一个与当前点赞数相同的
if (dp1[i] == dp1[num - 1]) {
minNoteNum = dp2[i];
break;
}
}
System.out.println(dp1[num - 1] + " " + minNoteNum);
}
}
}
试着将我们选中的题号,打印出来:
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
/**
* 试着将我们选中的题号,打印出来
* 4
* 1 2 3 1
*
* 5
* 2 3 2 3 2
*
* 7
* 5 1 1 5 1 1 5
*/
public class MainPlus {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int num = sc.nextInt(); //笔记数
int[] like = new int[num]; //点赞数
for (int i = 0; i < num; i++) {
like[i] = sc.nextInt();
}
if (num < 2) {
System.out.println(Math.max(like[0], like[1]) + " " + 1);
}
//根据题目给的两个规则,然后动态规划求解
int[] dp1 = new int[num]; //记录总点赞数
List[] noteLists=new List[num];//存放当前挑选了哪些笔记
/* 对List[]在=中的每个元素,进行初始化 */
for (int i = 0; i < num; i++) {
noteLists[i]=new ArrayList<>();
}
dp1[0] = like[0];
dp1[1] = Math.max(like[0], like[1]);
noteLists[0].add(0);
if (like[0]>like[1]){
noteLists[1].add(0);
}else {
noteLists[1].add(1);
}
for (int i = 2; i < num; i++) {
if (dp1[i - 2] + like[i] > dp1[i - 1]) { //注意大于的时候,才有必要更新,等于的时候,因为想要的文件最少,所以不用更新。
dp1[i] = dp1[i - 2] + like[i];
noteLists[i].addAll(noteLists[i-2]);
noteLists[i].add(i);
} else {
dp1[i] = dp1[i - 1];
noteLists[i].addAll(noteLists[i-1]);
}
}
int minNoteNum = noteLists[num-1].size();
String pickedNotes=noteLists[num-1].toString();;
//如果点赞数相同,返回文件个数较少的那个
for (int i = 0; i < num - 1; i++) { //顺序查找,找到的第一个与当前点赞数相同的
if (dp1[i] == dp1[num - 1]) {
minNoteNum = noteLists[i].size();
pickedNotes=noteLists[i].toString();
break;
}
}
System.out.println(dp1[num - 1] + " " + minNoteNum +" "+pickedNotes);
}
}
}
算法题3:
解法1:使用大顶堆
import java.util.*;
/**
* 解法1:二分查找+大顶堆
* 解题思路:
*
* 查找问题不难想到二分法。固定伤害的最小值是0,最大值一定是所有血量的最大值。
* 现在我们最难的问题就是判断给定伤害是不是合法。
*
*
* 对于是不是合法的问题,我们使用贪心策略,
* 每次从血量data中取最大值(所以使用最大堆存储血量),然后判断这个最大值可以消耗几次法术。
* 假设最大值是pre,伤害是mn,法力值是m,那么我们可以md=min(pre/mn,m)次法术。
* 接着我们需要将怪兽的剩余血量pre-md*mn添加到血量数组中data。
* 如果中间的过程中出现t(也就是可以攻击的次数)小于0的情况,那么自然就不合法了。
* 如果法力值m消耗完了,此时我们所有data值的和大于攻击次数t,那么自然不合法,否则一定合法。
*
* 我的理解:每次从队列里面取出当前血量最多的怪物,然后对其进行魔法伤害,之后将怪物的剩余血量再更新回队列中。
* 一直这样释放魔法攻击,直到法力值用光。因为一直选出的是当前血量最多的怪兽,所以即使伤害溢出了,那么伤害浪费也是最小的。
* 所以难点在于,怎么保证每次能从数组中,取出剩余血量最高的怪物
* PriorityQueue 默认是小顶堆
* PriorityQueue maxHeap=new PriorityQueue<>(Comparator.reverseOrder());//优先队列 默认最小堆 现在是最大堆
*
* 我的解法:使用优先队列,维护一个大顶堆。每次取出堆顶,然后对堆顶进行更新,在将这个结点插回堆里面,然后堆自动调整。这样我们的堆顶就又是最大元素了
*
*
* 当伤害mn合法的时候,那么说明>mn的伤害一定都合法,我们只需要在[l,mn]区间中找下一个即可;
* 否则,我们在[mn+1,r]区间中找。
*
* 输入:
* 3 4 3
* 5 2 1
* 输出:
* 3
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int N = sc.nextInt();
int T = sc.nextInt();
int M = sc.nextInt();
int[] H = new int[N];
for (int i = 0; i < N; i++) {
H[i] = sc.nextInt();
}
Arrays.sort(H);//对怪物的血量排序,那么H[H.length-1]就是血量最大值。
/* 二分查找一个X */
//当魔法伤害mid合法的时候,那么说明 大于mid的伤害 一定都合法,我们只需要在[low,mid]区间中找下一个即可;
//否则,我们在[mn+1,r]区间中找。
int low = 0;//x最小值是0,说明此时不需要使用魔法攻击
int high = H[N - 1];//X的上界是所有怪物的血量中的最大值
int mid = low;
while (low < high) {
mid = (low + high) / 2;
if (isSolution(mid, N, T, M, H)) {
high = mid;
} else {
low = mid + 1;
}
}
System.out.println(low);
}
}
/**
* 判断当前X是否是问题的一个解
*
* @param X
* @param N
* @param T
* @param M
* @param H
* @return
*/
public static boolean isSolution(int X, int N, int T, int M, int[] H) {
int count = 0;//回合数
/* 构造一个大顶堆。剩余血量最多的,永远放在堆顶 */
Queue maxHeap = new PriorityQueue<>(N, Comparator.reverseOrder());//声明一个大顶堆
for (int i = 0; i < H.length; i++) {
maxHeap.add(H[i]);
}
int remainingHP = 0;//怪物被攻击后的剩余血量
while (!maxHeap.isEmpty()) { //用物理攻击或者是魔法攻击,把所有的剩余血量都耗完
if (M > 0) { //如果还有魔法值,则使用魔法攻击,来攻击剩余的最大血量(最大堆的堆顶)
--M;
++count;//回合数加一
remainingHP = maxHeap.poll() - X;
if (remainingHP > 0) {//如果被魔法攻击后,还有剩余血量。则将这个剩余生命值,重新插入到大顶堆中,等待下一次被取出。
maxHeap.add(remainingHP);
}
} else {//如果没蓝了,直接使用物理攻击
++count;//回合数加一
remainingHP = maxHeap.poll() - 1;
if (remainingHP > 0) {//如果被魔法攻击后,还有剩余血量。则将这个剩余生命值,重新插入到大顶堆中,等待下一次被取出。
maxHeap.add(remainingHP);
}
}
}
if (count <= T) {
return true;
}
return false;
}
}
解法2:将血量分为整除倍数和余数,两个部分
import java.util.Arrays;
import java.util.Scanner;
/**
* 测试输入:
* 3 4 3
* 5 2 1
*
* 输出结果:
* 3
*
*
* 解法二:
* 首先将魔物血量分为两部分: X的倍数 和 余数。
* (1)若法力值M,大于当前的倍数,先全部用魔法攻击。若法力值小于 倍数,则剩余的全部需要使用物理攻击。
* (2)若法力值还有剩余,我们先把所有的余数从大到小排序。先不断使用魔法攻击,直到法力值耗光。若法力值还没耗光,余数数组已经都消灭了,则返回消耗的回合数。
* (3)将剩余的全部用物理攻击耗到0,然后返回回合数。
*/
public class Main2 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int N = sc.nextInt();
int T = sc.nextInt();
int M = sc.nextInt();
int[] H = new int[N];
for (int i = 0; i < N; i++) {
H[i] = sc.nextInt();
}
Arrays.sort(H);//对怪物的血量排序
//2.二分查找返回key(可能有重复)第一次出现的下标x,如果不存在返回-1
//当伤害mn合法的时候,那么说明>mn的伤害一定都合法,我们只需要在[l,mn]区间中找下一个即可;
// 否则,我们在[mn+1,r]区间中找。
int low = 1;//x最小值是0,说明此时不需要使用魔法攻击
int high = H[N - 1];//X的上界是所有怪物的血量中的最大值
int mid;
while (low < high) {
mid = low + (high - low) / 2;
if (isSolution(mid, N, T, M, H)) { //如果mid是可行解,那么接着在[low,mid]里面,尝试搜索第一个可行解。
high = mid;//high一直指向一个可行解
} else { //若 mid=right。在每次循环结束时,left总是x的第一个可能下标,array[right]总是第一个等于key或者大于key的元素。
//那么对应于left==right的情况,检查array[left]即可获得key是否存在,若存在则下标为x;
//对于left>right的情况,其实是不用考虑的。因为left==上一次循环的mid+1,而mid <= right。若mi+1>right,意味着mid == right,但此时必有left == right,这一轮循环从开始就不可能进入。
//运行至此,low=high,而high一直是就是我们之前找到的可行解。所以运行至此 low = high = 第一个可行解
System.out.println(low);//返回找到的最小的合法的X
}
}
/**
* 判断X是否是一个合法的解
*
* @param X
* @param N
* @param T
* @param M
* @param H
* @return
*/
public static boolean isSolution(int X, int N, int T, int M, int[] H) {
int sumOfHP = 0;
for (int i = 0; i < H.length; i++) {
sumOfHP = sumOfHP + H[i];
}
int[] timesArray = new int[N]; //倍数数组times
int[] remainderArray = new int[N]; //余数数组Remainder
Arrays.fill(timesArray, 0);
Arrays.fill(remainderArray, 0);
/* 把每个魔物的血量分为两块,分为X的倍数和余数 */
for (int i = 0; i < N; i++) {
remainderArray[i] = H[i] % X; //被X整除的余数
timesArray[i] = H[i] / X; //被X整除的次数
}
Arrays.sort(remainderArray); //将余数数组排序
int sumOfTimes = 0; //被X整除的次数之和
for (int i = 0; i < timesArray.length; i++) {
sumOfTimes = sumOfTimes + timesArray[i];
}
int sumOfRemainder = 0; //所有的余数之和
for (int i = 0; i < remainderArray.length; i++) {
sumOfRemainder = sumOfRemainder + remainderArray[i];
}
int mofaTimes = 0; //魔法攻击次数
int wuliTimes = 0; //物理攻击次数
if (sumOfTimes >= M) {//法力值只够在“整数部分”使用,“余数部分”不能使用法力了。
mofaTimes = M; //用完了所有法力
wuliTimes = sumOfHP - M * X; //魔法攻击后,剩余的血量,全部需要物理攻击
if ((mofaTimes + wuliTimes) <= T) { //若总回合数符合要求,则当前的X符合要求
return true;
}
} else { //如果法力值溢出了整数数组,那么每次从余数数组中取出一个最大的剩余血量,来使用魔法攻击,这样伤害溢出最小。
/* sumOfTimes= remainderArray.length) { //所有的余数数组,都能被法力秒杀。注意remainderArray.length其实就是N
mofaTimes = sumOfTimes + remainderArray.length;
wuliTimes = 0;//一路魔法攻击通关,用不上物理技能了
if (mofaTimes <= T) {
return true;
}
} else {//剩余的法力值,不足以消耗完“余数数组”,那么把剩余的几个最小的余数,使用物理攻击、
/* residualM < remainderArray.length */
mofaTimes = M;
/* 注意remainderArray之前是按从大到小的顺序排过序的。所以统计物理攻击次数时,只用累加前几个较小的剩余血量。因为后面较大的剩余血量,被魔法攻击干掉了。 */
for (int i = 0; i <= remainderArray.length - 1 - residualM; i++) {
wuliTimes = wuliTimes + remainderArray[i];
}
if ((mofaTimes + wuliTimes) <= T) {
return true;
}
}
}
return false;
}
}