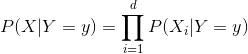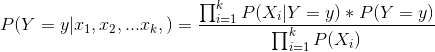朴素贝叶斯的三个常用模型：高斯、多项式、伯努利

部分内容转自：https://blog.csdn.net/qq_27009517/article/details/80044431

0.朴素贝叶斯

朴素贝叶斯分类（NBC，Naive Bayes Classifier）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X，求出使得后验概率最大的输出Y。

 

设样本数据集，

对应样本数据的特征属性集为，

类别集。

即D可以分为m种类别。其中相互独立同分布且随机。

那么Y的先验概率为P(Y)，Y的后验概率为P(Y|X)。由贝叶斯定理可以得到，后验概率可以由证据P(X)，先验概率P(Y)，条件概率P(X|Y)计算得出，公式如下所示：

换成分类的示意表达式：

朴素贝叶斯基于各个特征之间相互独立，在给定取值时，可以将上式进一步写为

因为P(X)的值是固定不变的，因此在比较后验概率时，只需要比较上式的分子即可。因此可以得到一个样本数据属于类别

的朴素贝叶斯计算如下图所示：

 

 

1.朴素贝叶斯-多项式

设某文档，是该文档中出现过的单词，允许重复。在多项式模型中，

先验概率P(c) = 类c下单词总数 / 整个训练样本的单词总数，

条件概率P(|c) = (类c下单词在各个文档中出现过的次数之和+1) / (类c下单词总数+m)。

在这里，m=|V|，p=1/|V|。V是训练样本的单词表（即抽取单词，单词出现多次，只算一个），|V|则表示训练样本包含多少种单词。

P(|c)可以看作是单词在证明d属于类c上提供了多大的证据，而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。

 

给定一组分类好了的文本训练数据，如下：

index	doc	China?
1	Chinese Beijing Chinese	yes
2	Chinese Chinese Shanghai	yes
3	Chinese Macao	yes
4	Tokyo Japan Chinese	no

给定一个新样本Chinese Chinese Chinese Tokyo Japan，对其进行分类。

该文本用属性向量表示为d=(Chinese, Chinese, Chinese, Tokyo, Japan)，类别集合为Y={yes, no}。

先验概率计算如下：

类yes下总共有8个单词，类no下总共有3个单词，训练样本单词总数为11，因此P(yes)=8/11, P(no)=3/11。

类条件概率计算如下：

P(Chinese | yes)=(5+1)/(8+6)=6/14=3/7               //类yes下单词Chinese在各个文档中出现过的次数之和+1 / 类yes下单词的总数(8)+总训练样本的不重复单词(6)

P(Japan | yes)=P(Tokyo | yes)= (0+1)/(8+6)=1/14

P(Chinese|no)=(1+1)/(3+6)=2/9

P(Japan|no)=P(Tokyo| no) =(1+1)/(3+6)=2/9

分母中的8，是指yes类别下doc的长度，也即训练样本的单词总数；

6是指训练样本有Chinese,Beijing,Shanghai, Macao, Tokyo, Japan 共6个单词；

3是指no类下共有3个单词。

有了以上类条件概率，开始计算后验概率，

   //Chinese Chinese Chinese Tokyo Japan

P(yes | d)>P(no | d)，因此，这个文档属于类别china。 

 

 

2.朴素贝叶斯-伯努利模型

先验概率

P(c)= 类c下文件总数/整个训练样本的文件总数

条件概率

P(|c)=(类c下包含单词tk的文件数+1) / (类c的文档总数+2)

在这里，m=2， p=1/2。

 

还是使用前面例子中的数据，

index	doc	China?
1	Chinese Beijing Chinese	yes
2	Chinese Chinese Shanghai	yes
3	Chinese Macao	yes
4	Tokyo Japan Chinese	no

新样本Chinese Chinese Chinese Tokyo Japan，对其进行分类。

类yes下总共有3个文件，类no下有1个文件，训练样本文件总数4，因此

先验概率

P(yes)=3/4,

类条件概率

P(Chinese | yes)=(3+1)/(3+2)=4/5

P(Japan | yes)=P(Tokyo | yes)=(0+1)/(3+2)=1/5

P(Beijing | yes)= P(Macao|yes)= P(Shanghai |yes)=(1+1)/(3+2)=2/5

P(Chinese|no)=(1+1)/(1+2)=2/3

P(Japan|no)=P(Tokyo| no) =(1+1)/(1+2)=2/3

P(Beijing| no)= P(Macao| no)= P(Shanghai | no)=(0+1)/(1+2)=1/3

有了以上类条件概率，开始计算后验概率，

P(yes | d)=P(yes)×P(Chinese|yes) ×P(Japan|yes) ×P(Tokyo|yes)×(1-P(Beijing|yes)) ×(1-P(Shanghai|yes))×(1-P(Macao|yes))

P(no | d)= P(no)×P(Chinese|no) ×P(Japan|no) ×P(Tokyo|no)×(1-P(Beijing|no)) ×(1-P(Shanghai|no))×(1-P(Macao|no))

P(yes | d)不属于类别china。

 

 

3.两个模型（多项式，伯努利）的区别

二者的计算粒度不一样，多项式模型以单词为粒度，伯努利模型以文件为粒度，因此二者的先验概率和类条件概率的计算方法都不同。

计算后验概率时，对于一个文档d，多项式模型中，只有在d中出现过的单词，才会参与后验概率计算，伯努利模型中，没有在d中出现，但是在全局单词表中出现的单词，也会参与计算，不过是作为“反方”参与的。

一般来说，如果一个样本没有特征，那么将不参与计算。不过下面的伯努利模型除外。

 

 

4.使用朴素贝叶斯分类器划分邮件

 

 

5.朴素贝叶斯-高斯模型

当特征是连续变量的时候，运用多项式模型就会导致很多（不做平滑的情况下），此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，应该采用高斯模型。

高斯模型假设这些特征所属于某个类别的观测值符合高斯分布。

有些特征可能是连续型变量，比如说人的身高，物体的长度。这些特征可以转换成离散型的值，比如如果身高在160cm以下，特征值为1；在160cm和170cm之间，特征值为2；在170cm之上，特征值为3。也可以这样转换，将身高转换为3个特征，分别是f1、f2、f3，如果身高是160cm以下，这三个特征的值分别是1、0、0，若身高在170cm之上，这三个特征的值分别是0、0、1。不过这些方式都不够细腻，高斯模型可以解决这个问题。

 

下面是一组人类身体特征的统计资料。

性别	身高（英尺）	体重（磅）	脚掌（英寸）
男	6	180	12
男	5.92	190	11
男	5.58	170	12
男	5.92	165	10
女	5	100	6
女	5.5	150	8
女	5.42	130	7
女	5.75	150	9

问：已知某人身高6英尺、体重130磅，脚掌8英寸，请问该人是男是女？ 

根据朴素贝叶斯分类器，计算下面这个式子的值。

P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)

这里的困难在于，由于身高、体重、脚掌都是连续变量，不能采用离散变量的方法计算概率。而且由于样本太少，所以也无法分成区间计算。怎么办？

这时，可以假设男性和女性的身高、体重、脚掌都是正态分布，通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，算出某一点的密度函数的值。 

比如，男性的身高是均值5.855、方差0.035的正态分布。所以，男性的身高为6英尺的概率的相对值等于1.5789（大于1并没有关系，因为这里是密度函数的值，只用来反映各个值的相对可能性）。

对于脚掌和体重同样可以计算其均值与方差。有了这些数据以后，就可以计算性别的分类了。

P(身高=6|男) x P(体重=130|男) x P(脚掌=8|男) x P(男)= 6.1984 x e-9

P(身高=6|女) x P(体重=130|女) x P(脚掌=8|女) x P(女)=5.3778 x e-4

可以看到，女性的概率比男性要高出将近10000倍，所以判断该人为女性。