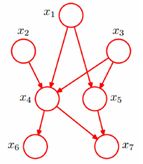
把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
贝叶斯网络(Bayesian Network),又称有向无环图模型(directed acyclic graphical model ,DAG),是一种概率图模型,根据概率图的拓扑结构,考察一组随机变量{X 1 ,X 2 ...X n }及其n组条件概率分布(Conditional Probability Distributions, CPD)的性质。
一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,它们可以是可观察到的变量,或隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系(或非条件独立)。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。
x1和x2独立,x6和x7在x4给定的条件下独立
x1,x2,…x7的联合分布图如下:
x1,x2,…x7的联合分布:
判断条件独立
1、通过贝叶斯网络判定条件独立
tail-to-tail
在c给定的条件下,a,b被阻断(blocked)是独立的
head-to-tail
在c给定的条件下,a,b被阻断(blocked),是独立的
head-to-head
在c未知的条件下,a,b被阻断(blocked),是独立的
2、将上述结点推广到结点集
D-separation:有向分离
对于任意的结点集A,B,C,考察所有通过A中任意结点到B中任意结点的路径,若要求A,B条件独
立,则需要所有的路径都被阻断(blocked),即满足下列两个前提之一:
1)A和B的“head-to-tail型”和“tail-to-tail型”路径都通过C;
2)A和B的“head-to-head型”路径不通过C以及C的子孙;
如果A,B不满足D-separation,A,B有时被称为D-connected.
链式网络
由D-separation可知,在xi给定的条件下,xi+1的分布和x1,x2…xi-1条件独立。即:xi+1的分布状态只和xi有关,和其他变量条件独立,这种顺次演变的随机过程模型,叫做马尔科夫模型。
Markov Blanket
一个结点的Markov Blanket是一个集合,在这个集合中的结点都给定的条件下,该结点条件独立于其他所有结点。
即:一个结点的Markov Blanket是它的parents,children以及spouses(孩子的其他parent)
贝叶斯网络的用途
诊断:P(病因|症状)
预测:P(症状|病因)
分类:max class P(类别|数据)
通过给定的样本数据,建立贝叶斯网络的拓扑结构和结点的条件概率分布参数。这往往需要借助先验知识和极大似然估计来完成。
在贝叶斯网络确定的结点拓扑结构和条件概率分布的前提下,可以使用该网络,对未知数据计算条件概率或后验概率,从而达到诊断、预测或者分类的目的。
贝叶斯网络的推导
贝叶斯网络的构建
依次计算每个变量的D-separation的局部测试结果,综合每个结点得到贝叶斯网络。
算法过程:
选择变量的一个合理顺序:X 1 ,X 2 ,...X n
对于i=1到n
在网络中添加X i 结点
在X 1 ,X 2 ,...X i-1 中选择X i 的父母,使得:
![]()
这种构造方法,显然保证了全局的语义要求:
举例说明:M, J, A,B,E
需要判断如下是否相等:
P(J|M) = P(J)
P(A|M,J) = P(A|M), P(A|M,J) = P(A|J), P(A|M,J) = P(A)
P(B|M,J,A) = P(B|M), P(B|M,J,A) = P(B|J), P(B|M,J,A) = P(B|A),…….
Tip:
先判断一个节点是否没有父节点,再判断节点只有一个父节点,再判断有两个父节点,第一次遇到等式成立,便可以确定节点的父节点,最多次判断的情况是前面的节点都是他的父节点。
压缩条件分布参数数目
Noisy-OR分布模型
节点U 1 ,U 2 ,...U k 是X的所有父节点;
有如下等式:
该模型的参数是关于父节点个数线性的。
举例:
该模型参数只需要3个参数即可表示所有的状态。这里是0.1, 0.2, 0.3
混合(离散+连续)网络
subsidy,buys均是离散的,harvest,cost均是连续的
需要定义一个条件概率密度函数,使用线性高斯模型:
cost随着harvest线性变化,方差不变
条件概率密度函数,也可使用sigmod函数
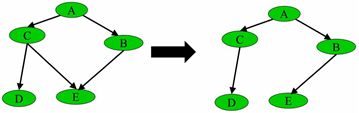
原贝叶斯网络的近似树结构
最大权生成树MSWT的建立过程
1.对于给定的分布P(x),对于所有的i≠j,计算联合分布P(xi|xj);
2.使用第1步得到的概率分布,计算任意两个结点的互信息I(Xi,Yj),并把I(Xi,Yj)作为这两个结点连接边的权值;
3.计算最大权生成树(Maximum-weight spanning tree)
a. 初始状态:n个变量(结点),0条边
b. 插入最大权重的边
c. 找到下一个最大的边,并且加入到树中;要求加入后,没有环生成。否则,查找次大的边;
d. 重复上述过程c过程直到插入了n-1条边(树建立完成)
4.选择任意结点作为根,从根到叶子标识边的方向;
5.可以保证,这课树的近似联合概率P'(x)和原贝叶斯网络的联合概率P(x)的相对熵最小。
两个结点间的互信息的计算公式: