洛谷P3373 【模板】线段树 2 #线段树#

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入格式

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入 #1复制

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出 #1复制

17
2

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

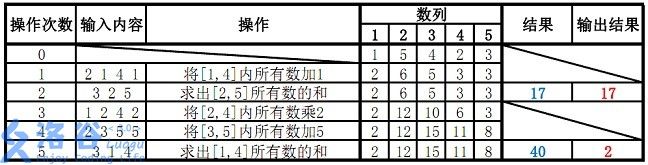
样例说明：

故输出应为17、2（40 mod 38=2）

题解

#include 
using namespace std;
typedef long long ll;

const int maxn = 1e5 + 10;
int n, m, p, opt, x, y;
ll k;
struct node
{
    int l, r;
    ll sum, mult, add;
    node() { l = r = sum = add = 0; mult = 1; }
} tree[maxn << 2];

inline int ls(int id) { return id << 1; }
inline int rs(int id) { return id << 1 | 1; }

void push_up(int id)
{
    tree[id].sum = (tree[ls(id)].sum + tree[rs(id)].sum) % p;
}

void push_down(int id)
{
    if (tree[id].add || tree[id].mult != 1)
    {
        tree[ls(id)].sum = (tree[ls(id)].sum * tree[id].mult + (tree[ls(id)].r - tree[ls(id)].l + 1) * tree[id].add) % p;
        tree[rs(id)].sum = (tree[rs(id)].sum * tree[id].mult + (tree[rs(id)].r - tree[rs(id)].l + 1) * tree[id].add) % p;
        tree[ls(id)].mult = tree[ls(id)].mult * tree[id].mult % p;
        tree[rs(id)].mult = tree[rs(id)].mult * tree[id].mult % p;
        tree[ls(id)].add = (tree[ls(id)].add * tree[id].mult + tree[id].add) % p;
        tree[rs(id)].add = (tree[rs(id)].add * tree[id].mult + tree[id].add) % p;
        tree[id].mult = 1;
        tree[id].add = 0;
    }
}

void build(int id, int l, int r)
{
    if ((tree[id].l = l) == (tree[id].r = r))
    {
        scanf("%lld", &tree[id].sum);
        return;
    }
    int mid = (l + r) >> 1;
    build(ls(id), l, mid);
    build(rs(id), mid + 1, r);
    push_up(id);
}

void mult(int id, int l, int r, ll x)
{
    if (tree[id].l == l && tree[id].r == r)
    {
        tree[id].sum = tree[id].sum * x % p;
        tree[id].mult = tree[id].mult * x % p;
        tree[id].add = tree[id].add * x % p;
        return;
    }
    push_down(id);
    int mid = (tree[id].l + tree[id].r) >> 1;
    if (r <= mid)
        mult(ls(id), l, r, x);
    else if (l > mid)
        mult(rs(id), l, r, x);
    else
    {
        mult(ls(id), l, mid, x);
        mult(rs(id), mid + 1, r, x);
    }
    push_up(id);
}

void add(int id, int l, int r, ll x)
{
    if (tree[id].l == l && tree[id].r == r)
    {
        tree[id].sum = (tree[id].sum + (r - l + 1) * x) % p;
        tree[id].add = (tree[id].add + x) % p;
        return;
    }
    push_down(id);
    int mid = (tree[id].l + tree[id].r) >> 1;
    if (r <= mid)
        add(ls(id), l, r, x);
    else if (l > mid)
        add(rs(id), l, r, x);
    else
    {
        add(ls(id), l, mid, x);
        add(rs(id), mid + 1, r, x);
    }
    push_up(id);
}

ll query(int id, int l, int r)
{
    if (tree[id].l == l && tree[id].r == r)
        return tree[id].sum;
    push_down(id);
    int mid = (tree[id].l + tree[id].r) >> 1;
    if (r <= mid)
        return query(ls(id), l, r);
    if (l > mid)
        return query(rs(id), l, r);
    return (query(ls(id), l, mid) + query(rs(id), mid + 1, r)) % p;
}

int main()
{
    scanf("%d%d%d", &n, &m, &p);
    build(1, 1, n);
    while (m--)
    {
        scanf("%d%d%d", &opt, &x, &y);
        switch (opt)
        {
            case 1:
                scanf("%lld", &k);
                mult(1, x, y, k);
                break;
            case 2:
                scanf("%lld", &k);
                add(1, x, y, k);
                break;
            case 3:
                printf("%lld\n", query(1, x, y));
        }
    }
    return 0;
}