算法设计与分析复习

1.动态规划

主要步骤：

1.找出最优解的性质，以刻画其结构特征
2.递归地定义最优值
3.自底向上计算最优值
4.构造最优解

• 1.0 动态规划算法的基本要素为：最优子结构和重叠子问题性质
• 1.1 不是动态规划算法基本步骤的是：找出最优解的解空间
• 1.2 动态规划法是自底向上，贪心算法自顶向下
• 1.3 备忘录方法是动态规划算法的变形
• 1.4 最长公共子序列算法利用的算法是动态规划法
• 1.5矩阵连乘问题的算法可由动态规划算法设计实现
• 1.6 动态规划解决01背包问题不需要排序

1.7 最大子段和算法

int MAXSum(int n, int a[])
{
    int sum = 0, b = 0;  //sum存储当前最大b[j], b存储当前值b[j]
    for(int i = 0; i < n; i++){
	if(b > 0) b += a[i];
	else b = a[i];  //一旦某个区段和为负，从下一个位置累和
	if (sum < b) sum = b;
    }
    return sum;
}

2贪心算法.

• 2.1能采用贪心算法求最优解的问题，一般具有的重要性质：最优子结构性质和贪心选择性质
• 2.2 哈夫曼编码的贪心算法所需的计算时间为nlogn
• 2.3 背包问题的贪心算法所需的计算时间为nlogn
• 2.4 背包问题的贪心算法

void Knapsack(int n, float M, float v[], float w[], float x[])
M:背包容量 v：价值 w：重量 x：装入份额
{
  Sort(n,v,w);  //把重量，价值进行排序
  int i;
  for(i = 1; i <= n; i++) x[i] = 0;
  float c = M;
  for(i = 1; i <= n; i++){
      if(w[i] > c) break; // 背包容量不够
      x[i] = 1;  //全部装入
      c -= w[i];  //背包容量减少
  }
  if(i <= n) x[i] = c/w[i]  //能装入多少

}

• 2.5 贪心算法求活动安排问题：

void GreedySelector(int n, Type s[], Type f[], bool A[])
A: 是否可以开始 n：活动场数 s：开始时间 f：结束时间
当s[i]>=f[j]时，活动相容
{
    A[1] = ture;  //第一场正常举行
    int j = 1;
    for(int i = 2; i <=n; i++){
	if(s[i] >= f[j]){  //下一次开始时间在上一场结束后
	    A[i] = ture;
	    j = i;
	}
	else A[i] = false;
    }
}

3.回溯法

• 3.0回溯法在问题的解空间中，按深度优先策略，从根节点出发搜索解空间树

• 3.1回溯法解旅行售货员问题时的解空间树是子集树

• 3.2 回溯法的效率不依赖确定解空间的时间

• 3.3 避免无效搜索采取：剪枝函数（约束函数 、 限界函数）

• 3.4 背包问题的回溯算法所需的计算时间为n2^n（要排序）

• 3.5 既带有系统性，又带有跳跃性的搜索算法

• 回溯法搜索子集树算法：

//如果满足约束函数和限界函数，赋值后进入下一层。当整棵树都遍历完后输出当前子集树
void backtrack(int t){ //t为当前层数
    if(t >=n)  //n可视为总层数
	output(x); //输出当前可行解x（0/1)
    else{
	for(int i = 0; i <=1; i++)
	    x[t] = i;
	    if(constraint(t) && bound(t))  //约束函数和限界函数都成立
		backtrack(t+1); //下一层
    }
}

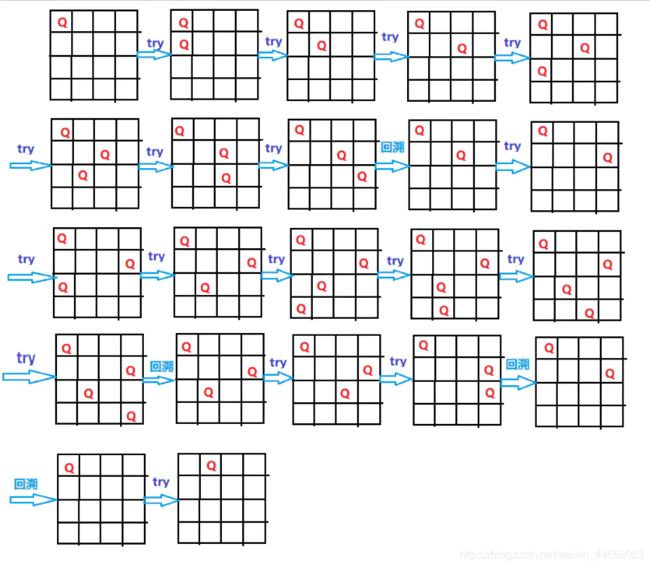
n皇后回溯法：
bool Queen::Place(int k){
//判断x[k]位置是否合法
    for(int j = 1; j < k; j++){ //对角或同列
	if((abs(k-j) == abs(x[j]-x[k])) || (x[j] == x[k])) return false
				对角							同列
	else return true;
    }
}

void Queen::Backtrack(int t){
    if(t > n) sum++;  //符合n皇后的方法数量
    else{
	for(int i = 1; i < t; i++){
	    x[t] = i;
	    if(约束条件) Backtrack(t+1);
	}
    }
}

4.

5. 分治法

基本思想

将一个规模为n的问题分解为k个规模较小的子问题，这些子问题相互独立且与原问题相同。递归的解这些子问题，然后将各个子问题的解合并得到原问题的解。

• 5.1 二分搜索算法利用分治策略实现

二分搜索算法：
int BinarySearch(Type a[], const Type& x, int n){
    int left = 0, right = n-1;
    while(left < right){
	    int middle = (left+right)/2;
	    if(x == a[middle]) 
	        return middle
	    if(x > a[middle]) 
	        left = middle+1;
	    else right = middle-1;
    }
}
return -1;
时间复杂性为O(logn)

• 5.2 实现循环赛日程表利用的算法是分治策略

• 5.3实现棋盘覆盖算法利用的算法是分治法

• 5.4 Strassen矩阵乘法是利用分治策略实现的

• 5.5 分治策略不需满足子问题一样

• 5.6 实现大整数的乘法是利用分治策略

• 5.7 快速排序算法基于分治策略

• 5.8 快速排序

void QuickSort(Type a[], int p, int r)
{
    if(p < r){
	int q = Partition(a, p, r);
	QuickSort(a, p, q-1);
	QuickSort(a, q+1, r);
    }
}

• 5.9 分治法能解决的问题的特征：
  1.问题规模缩小到一定程度可以很容易被解决
  2.该问题具有最优子结构性质
  3.分解出来的子问题的解合并即为该问题的解
  4.子问题之间相互独立

• 5.10 合并排序:

void MergeSort(Type a[], int left, int right){
    if(left

6.分支限界法

• 6.1最大效益优先（最小损耗优先)或广度搜索优先是分支限界法的搜索方式
• 6.2 分支限界法解决最大团问题，或节点表的组织形式是：最大堆
  
• 最大团问题：

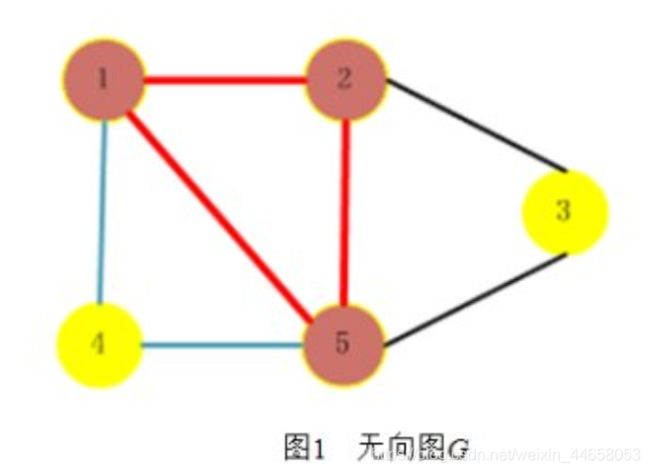
//以上图为例子，其实就是先选住1，2，到3的时候发现和1没相连，所以3不行
//到4，24，34没连通，不行
//到5，15，25，45都连通了，于是第一个最大团就是125

void Backtrack(int i){
    if(i > n){ //n为元素个数，i为当前层数
//如：1->2->3->4->5的搜索顺序，1的i为2，因为前面有一个活结点连接着12345.
	for(int j = 1; j <= n; j++){
	    bestx[j] = x[j];  //记录最大团的每个元素
	}
	bestn = cn;  //最大团的元素为当前团的元素
	return;
    }
    
    bool Ok = true;  //检查边是否连通
    for(int j = 1; j < i; j++){
	if(x[j] && !a[i][j]) Ok = false;  
//如果当前结点为可用结点，但连接两点的边不通，Ok为false
    }
    if(Ok){  //进入左子树
	cn++;  //结点数+1
	x[i] = 1;  //当前结点可用
	Backtrack(i+1);  //寻找下一个数
	cn--;  //返回上一个结点，结点数-1
    }
    if(cn+n-i > bestn){  //进入右子树
	x[i] = 0; //上一个已经用过的结点剪掉
	Backtrack(i+1);  //开始进入右子树搜寻
    }
}

• 6.3 分支限界法解决旅行售货员问题，活结点表的组织形式是最小堆(要排序)

• 6.4分支限界法设计算法的步骤：
  1.根据问题定义解空间
  2.确定易于搜索的解空间结构
  3.以广度优先或最大效益优先的方式搜索解空间，并用剪枝函数避免无效搜索

• 6.5常见的两种分支限界法的算法框架
  1.队列式分支限界法，按照队列先进先出的原则选取下一个结点为扩展结点
  2.优先队列分治限界法，按照优先队列，选取优先级最高的结点为当前扩展结点

• 6.6 分支限界法的搜索策略：
  在扩展结点处，先生成所有子节点，然后在当前活结点表中选择下一个结点作为扩展结点。为了提高搜索速度，计算一个函数（限界)，根据函数值，在活结点表中选择下一个结点作为扩展结点，使搜索向最优解的分支推进，以便更早找到最优解

7.全排列问题：

void perm(Type list[], int k, int m){
    if(k == m){
	for(int i = 0; i < m; i++) 输出list[i];
    } //输出当前排列
    else{	//最先交换的是3，3，然后交换3，4
	for(int i = k; i<=m; i++){ //产生多个排列
	    swap(list[k], list[i]);  //最先输出的时候k为3，交换3，3等于没有
	    perm(list, k+1, m);   //最先输出的是perm(list,4,4)
	    swap(list[k], list[i]);
	}
    }
}

8.分治法和动态规划法的异同点：

相同：将待求解的问题分解成若干个子问题，先解子问题，然后从这些子问题的解得到原问题的解
不同：动态规划的子问题不是相互独立的，分治法的子问题相互独立

9.回溯法和分支限界法的异同：

相同：都是一种在问题的解空间树T中搜索问题解的算法
不同：
1.搜索方式不同：回溯法是深度优先 分支限界是广度优先
2.存储空间的要求不同：回溯法是堆栈，分支限界是队列
3.结点的存储特性：回溯法活结点的所有可行子节点被遍历后才从栈中弹出 ；分治限界，每个结点只有一次成为活结点的机会
4.求解目标不同：回溯法适用满足约束条件的全部解； 分支限界满足约束条件的特定解