算法设计与分析---第3章 递归与分治策略
分治法的设计思想是,将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。 如果原问题可分割成k个子问题(1<k≤n),且这些子问题都可解,并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。 由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。
3.1 递归算法
程序直接或间接调用自身的编程技巧称为递归算法(Recursion)。
递归需要有边界条件、递归前进段和递归返回段。
- 当边界条件不满足时,递归前进;
- 当边界条件满足时,递归返回。
- 注意:在使用递增归策略时,必须有一个明确的递归结束条件,称为递归出口,否则将无限进行下去(死锁)。
递归的缺点:
- 递归算法解题的运行效率较低。
- 在递归调用过程中,系统为每一层的返回点、局部变量等开辟了堆栈来存储。递归次数过多容易造成堆栈溢出等。
3.1.1 Fibonacci数列
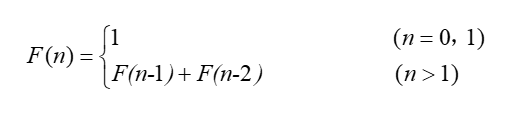
算法3.1 Fibonacci数列的递归算法
int fib(int n)
{
if (n<=1)
return 1;
return fib(n-1)+fib(n-2);
}该算法的效率非常低,因为重复递归的次数太多。
算法3.2 Fibonacci数列的递推算法
int fib[50];
void fibonacci(int n)
{
fib[0] = 1;
fib[1] = 1;
for (int i=2; i<=n; i++)
fib[i] = fib[i-1]+fib[i-2];
}void Perm(int list[], int k, int m)
{
if(k==m)
{
for(int i=0;i<=m;i++)
cout<<list[i]<<" ";
cout<<endl;
}
else
for(int j=k;j<=m;j++)
{
swap(list[k],list[j]);
Perm(list,k+1,m);
swap(list[k],list[j]);
}
}3.1.3 整数划分问题
整数划分问题是算法中的一个经典命题之一。把一个正整数n表示成一系列正整数之和: n=n1+n2+…+nk(其中,n1>=n2>=…>=nk>=1,k>=1)
正整数n的这种表示称为正整数n的划分。正整数n的不同划分个数称为正整数n的划分数,记作p(n) 。
正整数6有如下11种不同的划分,所以p(6)=11。
6
5+1
4+2, 4+1+1
3+3, 3+2+1, 3+1+1+1
2+2+2, 2+2+1+1, 2+1+1+1+1
1+1+1+1+1+1
算法分析

算法3.4 正整数n的划分算法
int split(int n,int m)
{
if(n==1||m==1)
return 1;
else if (n<m)
return split(n,n);
else if(n==m)
return split(n,n-1)+1;
else
return split(n,m-1)+split(n-m,m);
}3.2 分治策略
分治策略是对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同。
递归地解这些子问题,然后将各子问题的解合并得到原问题的解。
3.2.1 分治法的基本步骤
分治法在每一层递归上都有三个步骤:
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题;
- 合并:将各个子问题的解合并为原问题的解。
算法3.5 分治策略的算法设计模式
Divide_and_Conquer(P)
{
if (|P|<=n0 )
return adhoc(P);
divide P into smaller substances P1,P2,…,Pk;
for (i=1; i<=k; k++)
yi=Divide-and-Conquer(Pi)
Return merge(y1,y2,…,yk)
}在用分治法设计算法时,最好使子问题的规模大致相同。如分成大小相等的k个子问题,许多问题可以取k=2。 这种使子问题规模大致相等的做法是出自一种平衡(Balancing)子问题的思想,它几乎总是比子问题规模不等的做法要好。
3.2.2 分治法的适用条件
分治法所能解决的问题一般具有以下几个特征:
- 该问题的规模缩小到一定的程度就可以容易地解决;
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
- 利用该问题分解出的子问题的解可以合并为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
3.2.4循环赛日程表
问题描述:设有n=2k个运动员要进行网球循环赛。
现要设计一个满足以下要求的比赛日程表:
- 每个选手必须与其他n-1个选手各赛一次;
- 每个选手一天只能参赛一次;
- 循环赛在n-1天内结束。
请按此要求将比赛日程表设计成有n行和n-1列的一个表。 在表中的第i行,第j列处填入第i个选手在第j天所遇到的选手,其中1≤i≤n,1≤j≤n-1。
void Table(int k)
{
int i, r;
int n = 1 << k;
for (i=0; i<n; i++)
a[0][i] = i + 1;
for (r=1; r<n; r<<=1)
for (i=0; i<n; i+=2*r)
{
Copy(r, r + i, 0, i, r);
Copy(r, i, 0, r + i, r);
}
}实现方阵的拷贝
//源方阵的左上角顶点坐标(fromx, fromy),行列数为r
//目标方阵的左上角顶点坐标(tox, toy),行列数为r
void Copy(int tox, int toy, int fromx, int fromy, int r)
{
for (int i=0; i<r; i++)
for (int j=0; j<r; j++)
a[tox+i][toy+j] = a[fromx+i][fromy+j];
}3.2.6 选择问题
对于给定的n个元素的数组a[0:n—1],要求从中找出第k小的元素。
输入
输入有多组测试例。
对每一个测试例有2行,第一行是整数n和k(1≤k<n≤1000),第二行是n个整数。
输出
第k小的元素。
利用快速排序算法的思想,来解决选择问题。
记一趟快速排序后,分解出左子集中元素个数为 nleft,则选择问题可能是以下几种情况之一:
- nleft =k﹣1,则分界数据就是选择问题的答案。
- nleft >k﹣1,则选择问题的答案继续在左子集中找,问题规模变小了。
- nleft <k﹣1,则选择问题的答案继续在右子集中找,问题变为选择第k-nleft-1 小的数,问题的规模变小了。
算法3.9 采用分治策略找出第k小元素的算法
int select(int left,int right,int k)
{
if(left>=right)
return a[left];
int i=left;
int j=right+1;
int pivot=a[left];
while(true)
{
do{
i=i+1;
}while(a[i]<pivot);
do{
j=j-1;
}while(a[j]>pivot);
if(i>=j)
break;
swap(a[i],a[j]);
}
if(j-left+1==k)
return pivot;
a[left]=a[j];
a[j]=pivot;
if(j-left+1<k)
return select(j+1,right,k-j+left-1);
else
return select(left,j-1,k);
}3.2.7输油管道问题
某石油公司计划建造一条由东向西的主输油管道。该管道要穿过一个有n口油井的油田。从每口油井都要有一条输油管道沿最短路经(或南或北)与主管道相连。
如果给定n口油井的位置,即它们的x坐标(东西向)和y坐标(南北向),应如何确定主管道的最优位置,即使各油井到主管道之间的输油管道长度总和最小的位置?
给定n口油井的位置,编程计算各油井到主管道之间的输油管道最小长度总和。
输入
第1行是一个整数n,表示油井的数量(1≤n≤10 000)。 接下来n行是油井的位置,每行两个整数x和y (﹣10 000≤x,y≤10 000)。
输出
各油井到主管道之间的输油管道最小长度总和。
设n口油井的位置分别为pi=(xi, yi) ,i=1~n。由于主输油管道是东西向的,因此可用其主轴线的y坐标唯一确定其位置。主管道的最优位置y应该满足:
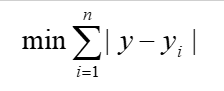
由中位数定理可知,y是中位数。
算法1:对数组a排序(一般是升序),取中间的元素
int n;
int x;
int a[1000];
cin>>n;
for(int k=0;k<n;k++)
cin>>x>>a[k];
sort(a,a+n);
int min=0;
for(int i=0;i<n;i++)
min += (int)fabs(a[i]-a[n/2]);
cout<<min<<endl;算法2:采用分治策略求中位数
int n;
int x;
int a[1000];
cin>>n;
for (int i=0; i<n; i++)
cin>>x>>a[i];
int y = select(0, n-1, n/2);
int min=0;
for(int i=0;i<n;i++)
min += (int)fabs(a[i]-y);
cout<<min<<endl;3.2.8 半数集问题
给定一个自然数n,由n开始可以依次产生半数集set(n)中的数如下。
(1) n set(n);
(2) 在n的左边加上一个自然数,但该自然数不能超过最近添加的数的一半;
(3) 按此规则进行处理,直到不能再添加自然数为止。
例如,set(6)={6,16,26,126,36,136}。
半数集set(6)中有6个元素。
注意半数集是多重集。
对于给定的自然数n,编程计算半数集set(n)中的元素个数。
设set(n)中的元素个数为f(n) ,则显然有:

算法3.12 计算半数集问题的递归算法
int comp(int n)
{
int ans=1;
if (n>1)
for(int i=1;i<=n/2;i++)
ans+=comp(i);
return ans;
}算法3.13 计算半数集问题的递归算法—记忆式搜索
int a[1001];
int comp(int n)
{
int ans=1;
if(a[n]>0)
return a[n];
for(int i=1;i<=n/2;i++)
ans+=comp(i);
a[n]=ans;
return ans;
}