自适共振神经网络算法 ART 算法 代码实现

---

自适共振神经网络算法 ART1 算法python 代码实现

---

由于学习需要ART算法，python 和matlab 又没有直接调用的模块和函数，故自己写了一个简单易懂、快捷优化了的ART1 算法，代码一共80行左右，附带详细解析，如下：

# coding=utf-8
import numpy as np


# 初始化内心向量矩阵B 和外星向量矩阵T （每一列标识一个 内星/外星 向量）
# 内星向量是C层传入R层的权值 ，外星向量是R层记录模式的向量，R层反馈给C层
def Set_B0_T0(n):
    b = 1 / (1 + n)
    B = []
    T = []
    for i in range(n):
        B.append(b)
        T.append(1)
    # 先构造 一列初始向量，再将向量矩阵化（因为后续的算法针对矩阵化的 matrix类型进行）
    # numpy的mat函数就是将向量转化成矩阵的
    B = np.mat(B)
    T = np.mat(T)
    # 矩阵.T 表示矩阵的转置，将一行转成一列了（因为我是用列来表示 内\外 星向量的）
    B = B.T
    T = T.T
    return B, T


# 当竞争获胜向量匹配成功后，才有权力改变它的 内\外星向量权值
# 参照书本给的方式，定义权值改变函数
def AdjustBT(B, T, x, j):
    x = np.mat(x)
    xigama_TX = x * T[:, j]  # 矩阵*矩阵= 表示矩阵乘法
    xigama_TX = xigama_TX[0, 0]
    B[:, j] = np.multiply(T[:, j], x.T) * (1 / (0.5 + xigama_TX))
    T[:, j] = np.multiply(T[:, j], x.T)  # np.multiply 是矩阵点乘
    return B, T


# 定义 竞争函数，选取R层竞争获胜的向量；由于每次只选一个竞争获胜的向量，再配对不成功的回调过程中
# 会造成Python代码十分麻烦的内嵌函数形式，所以我直接比较他们并且排序，返回一个按大小顺序排列的索引 list
# 如果需要回调，我直接再这个list 里面依次选择就行了 ，十分方便
def Competitor(B, x):
    x = np.mat(x)  # x参数开始是一个list ，因为矩阵运算需要 务必将其转成矩阵形式
    J = B.shape[1]  # J算出矩阵的列数 shape 返回一个二元元组，表示行数和列数 选取第二个即可
    competition = []  # 用于接收x与每个内星向量的乘积和，方便后续比较
    for j in range(J):
        compe = x * B[:, j]  # x与每个内星向量的乘积和
        competition.append(compe[0, 0])
    competition = np.array(competition)  # 只有array 类型才能直接抽取按大小排序后的索引
    j_order = np.argsort(-competition)  # 按大小排序后的索引
    j_order = list(j_order)  # 由于后边要用j_order 循环所以又要转会List类型
    return j_order


# 竞争成功的R层节点，通过外星向量和x 匹配，rou0是设置的匹配度大小
def Match(T, x, j, rou0):
    N0 = sum(x)
    x = np.mat(x)
    N = x * T[:, j]
    N = N[0, 0]  # 由于N是一个（1x1）矩阵 所以要提取其中的值
    rou = N / N0
    if rou >= rou0:  # 按照匹配原则，大于设定匹配度的算匹配成功
        matchBOOL = True
    else:
        matchBOOL = False
    return matchBOOL


# 当所有R层节点匹配不成功，要曾加一个R层节点，增加节点的内\外星向量
def ADD_BT(B, T, x, n):
    b = x  # 内星向量设为x
    b = np.mat(b).T
    B = np.hstack((B, b))  # 原来的B 与 新增的内星列向量进行拼接
    L = [1] * n  # 外星向量设为 1
    L = np.mat(L).T
    T = np.hstack((T, L))
    return B, T


# 根据匹配是否成功进行归类
def Group(B, T, x, j_order, Groups, rou0, n):
    success = 0
    for j in j_order:  # 对j_order 进行依次匹配
        matchBOOL = Match(T, x, j, rou0)
        if matchBOOL:  # 若x在这个j节点匹配成功，这个组加上这个x
            B, T = AdjustBT(B, T, x, j)
            jj = j + 1
            if jj not in Groups:  # 在字典加东西的 一贯手法
                Groups[jj] = [x]
            else:
                Groups[jj].append(x)
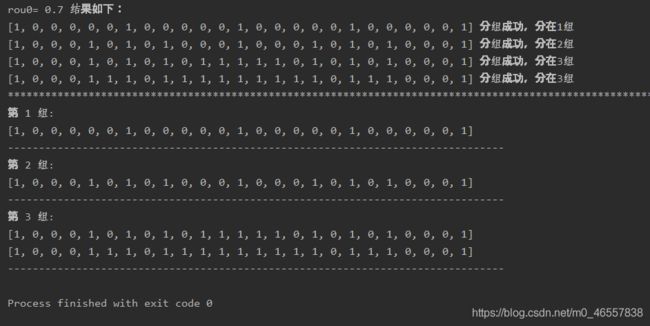
            print(x, '分组成功，分在{}组'.format(jj))
            success = 1  # 匹配成功，success变成1 不再进行后面操作
            break
    if success == 0:  # 如果匹配不成功
        B, T = ADD_BT(B, T, x, n)  # 增加R层一个节点
        jj = B.shape[1]  # 获取最后一列的索引，它肯定就是只会的匹配成功节点了
        B, T = AdjustBT(B, T, x, jj - 1)  # 匹配成功就调整相应内外星向量
        Groups[jj] = [x]
        print(x, '分组成功，分在{}组'.format(jj))
    return B, T, Groups


# 主函数
def ART(train_X, rou0):
    n = len(train_X[0])  # 取x的维数
    Groups = {
     }  # 初始分组
    B, T = Set_B0_T0(n)  # 初始B、T
    for x in X:  # 对每一个x进行判断归类
        j_order = Competitor(B, x)  # 竞争
        B, T, Groups = Group(B, T, x, j_order, Groups, rou0, n)  # 分组
    print('*****' * 30)

    # 以下是显示分组结果
    for key, value in Groups.items():
        print('第', key, '组:')
        for x in value:
            print(x)
        print('----' * 20)


rou0 = 0.7
X = [[1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1],
     [1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1],
     [1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1],
     [1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1]]
n = len(X)
ART(X, rou0)