左神算法基础class1——例子1遍历、二分、外排
左神算法基础class1——例子1遍历、二分、外排
- 题目:一个有序数组A,另一个无序数组B,请打印B中的所有不在A中的数,A数组长度为N,B数组长度为M。
-
- 1.算法流程1:遍历查找
-
- (1)分析
- (2)完整代码
- (3)复杂度分析
- 2.算法流程2:二分查找
-
- (1)分析
- (2)完整代码
- (3)复杂度分析
- 3.算法流程3:类似外排
-
- (1)分析
- (2)外排代码
- (3)辅助代码
- (4)完整代码
- (5)复杂度分析
题目:一个有序数组A,另一个无序数组B,请打印B中的所有不在A中的数,A数组长度为N,B数组长度为M。
算法流程1:对于数组B中的每一个数,都在A中通过遍历的方式找一下;
算法流程2:对于数组B中的每一个数,都在A中通过二分的方式找一下;
算法流程3:先把数组B排序,然后用类似外排的方式打印不在A中出现的数;
1.算法流程1:遍历查找
算法流程1:对于数组B中的每一个数,都在A中通过遍历的方式找一下。
(1)分析
1.把B在A中遍历,使用两个for循环,B在外侧,A在内侧,顺序不能反了。
2.需要有判断是否存在,如果两个数相同直接break;由于如果相等直接跳出,则每一轮最后判断if(j==A_MAX-1),相等表示最后一轮也不相等,输出B
int j;
for(int i = 0;i < B_MAX;i++)
{
for(j=0;j < A_MAX;j++)
{
if(b[i]==a[j])
{
break;
}
if(j==A_MAX-1)
cout<<b[i]<<' ' ;
}
}
}
3.随机数生成器,使用#include头文件,函数内使用srand((unsigned)time(NULL))生成系统时间的随机数;调用时,用 rand()调用,如果要生成[a,b]之间的随机数,则a+rand()%(b-a+1)。
a[i] = rand()%10;//a生成0-9之间的数
(2)完整代码
#include (3)复杂度分析
遍历B[0,M-1],遍历A[0,N-1],故O(M*N)
2.算法流程2:二分查找
算法流程2:对于数组B中的每一个数,都在A中通过二分的方式找一下;
(1)分析
1.外循环是B的数,每个数都需要遍历,此外,遍历考开始时需要重新初始化L,R,M
for(int i = 0;i < B_MAX;i++)
{
int L = 0;
int R = A_MAX - 1;
int M = L+(R-L)/2; //L+(R-L)>>1防止越界
。。。
2.for内部用while(Lif(L>R)判断并输出B。
while (L<=R)
{
if(b[i] < a[M])
R = M-1;
else if(b[i] > a[M])
L = M+1;
else
break;
M = L+(R-L)/2;
}
if(L>R)
cout<<b[i]<< ' ';
(2)完整代码
#include (3)复杂度分析
二分法寻址,N一次一半,复杂度为logN(以2为底),B中所有元素遍历一遍需要M次,则O(M*logN)
3.算法流程3:类似外排
算法流程3:先把数组B排序,然后用类似外排的方式打印不在A中出现的数;
(1)分析
1.把A,B都排好,指针都指向首位
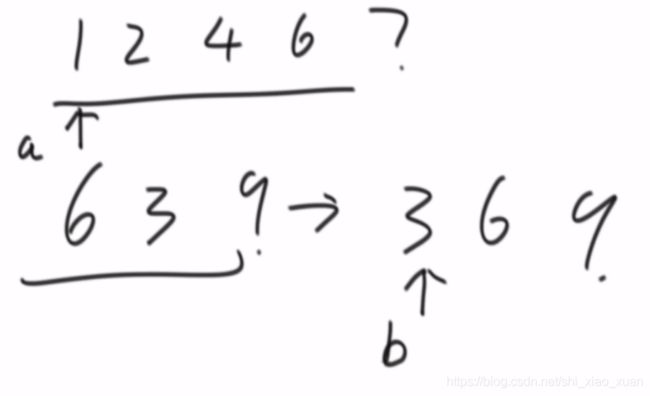
2.a小于b移动a,如果a>b,则B没在A中,打印B
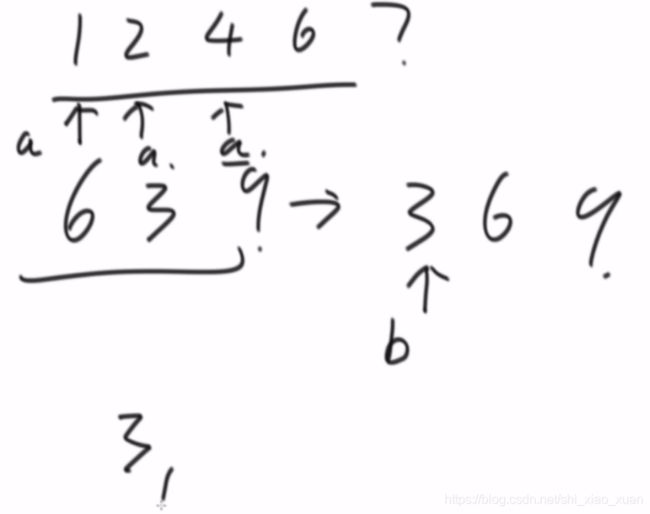
3.b后移,继续a小移动a,如果a=b则,b后移
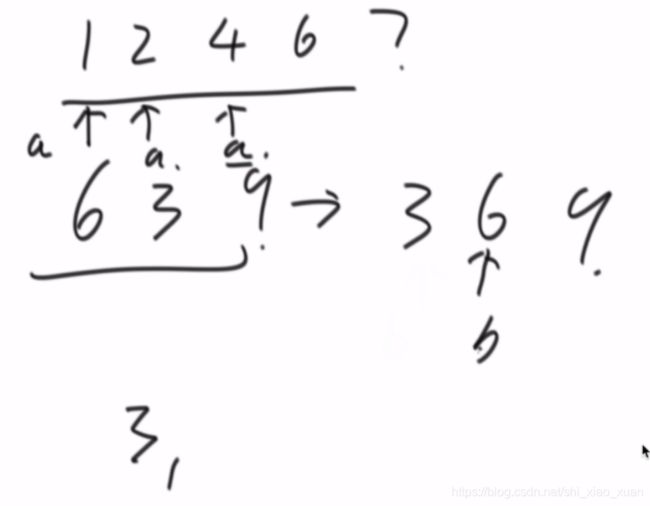
总结:
1.b
3.b>a时,a后移
(2)外排代码
while循环判断条件:A,B都没到达末尾
while循环之后:如果B还没完且B的后一位不等于前一位则把B剩余的直接输出,如果B的后一位和前一位相同,B再次后移(防止a = 1,3,4,5,b=2,3,3,4,5,5时,输出B中最后一个5)
int a_pos = 0;
int b_pos = 0;
while(a_pos<A_MAX && b_pos<B_MAX)
{
if(a[a_pos]<b[b_pos])
{
a_pos++;
}
else if(a[a_pos]==b[b_pos])
{
b_pos++;
}
else
{
cout<<b[b_pos++]<<" ";
}
}
while(b_pos!=B_MAX)
{
if(b[b_pos] == a[a_pos])
{
b_pos++;
break;
}
cout<<b[b_pos++]<<" ";
}
(3)辅助代码
1.生成A,B的随机数
srand((unsigned)time(NULL));
//初始化a,b
int a[A_MAX];
int b[B_MAX];
for(int i = 0;i < A_MAX;i++)
{
a[i] = rand()%10;
}
Sleep(1000);
for(int i = 0;i < B_MAX;i++)
{
b[i] = rand()%9;
}
2.冒泡排序(非必须此算法)
for(int i = 0;i < B_MAX-1;i++)
{
for (int j = 0;j < B_MAX-1-i;j++)
{
if(b[j] > b[j+1])
{
exchange(b[j],b[j+1]);
}
}
}
for(int i = 0;i < A_MAX-1;i++)
{
for (int j = 0;j < A_MAX-1;j++)
{
if(a[j] > a[j+1])
{
exchange(a[j],a[j+1]);
}
}
}
3.交换冒泡的数字:必须用引用,否则形参不会改变实参
void exchange(int &x,int &y)
{
int temp = x;
x = y;
y = temp;
}
4.输出a,b
cout<<"a = ";
for(int i = 0;i < A_MAX;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
cout<<"b = ";
for(int i = 0;i < B_MAX;i++)
{
cout<<b[i]<<" ";
}
cout<<endl;
(4)完整代码
#include (5)复杂度分析
a最大走N,b最大走M,则最差情况O(N+M),排序时本题为冒泡O(M2),其他最快O(MlogM),和为O(N+M)+O(MlogM)。