算法基础(一):枚举
慕课:程序设计与算法(二)算法基础 郭玮老师课程的学习笔记
枚举,基于逐个尝试答案的一种文体求解策略,根据所有可能的情况,并且一一判断。
大家可能会说枚举不就是一种简单的将数据全都遍历一遍吗,但是在这里我们将枚举进行优化,让枚举更加聪明,从而达到算法的目的,即提供更快更好的解题的方法,这样枚举就不是一种简单的遍历,而是一种高大上的算法方法。
枚举也并不是每一种可能都需要尝试,可以根据题目的要求按照从小到大的遍历顺序、或者对枚举的范围进行限定,从而减小枚举的次数、时间等,从而进行优化算法。
同时,题目有时没有给出明确的枚举条件,我们需要从题目中找出需要枚举的量及枚举的范围。
1、例题:完美立方
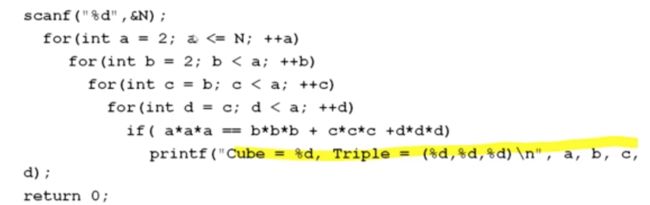
对于这一题,简单的求解就是可以对a<=100,b<=100,c<=100,d<=100进行四层循环嵌套,a在最外面,d在最里层,如果结果满足且b<=c<=d则输出。但是我们会发现对于那种b<=c<=d的情况完全可以不进行计算,而直接排除,减少计算的次数,如图
这里我们直接对循环遍历的范围进行限定,a的枚举范围为[2,N],b的枚举范围为[2,a-1],c的枚举范围为[b,a-1],d的枚举范围为[c,a-1],b、c、d直接限定最大值小于a,并且c、d开始的最小值限定在b和c,可以自动满足b<=c<=d这个条件,但是从次数上可以减少很多,从而优化计算。
2、生理周期
简单的尝试思路,就是可以对d+1开始直到21252天,每天尝试是否是23、28、33的倍数,但是这样尝试需要遍历20000多次,如图,我们该怎么提高枚举效率
我们知道三天同时出现高峰期时必须是体力的高峰期,所以我们首先找体力的高峰期,即每23天一个循环,再找体力高峰期出现的日子里是不是情商的高峰期,即是不是每28天一个循环,差为28的倍数,如果是则证明即时体力的高峰期又是情商的高峰期,接下来就判断是不是智商的高峰期,即差是不是33的倍数;否则,加23,移到下一个体力的高峰期,直到找到一个体力和情商的双高峰期,然后判断智商的高峰期。智商同理,如果不是智商的高峰期,则需要移到下一个体力和情商的高峰期,加23*28;否则输出,即三个的高峰期。
优化算法,只有在体力高峰期的时候才需要判断是不是情商的高峰期,即每隔23天判断情商高峰期,如果是情商高峰期,则判断智商高峰期,如果不是智商高峰期,则每隔23*28即体力和情商双高峰期时才判断体力高峰期。
3、称硬币
给出称的结果前提下找真假币,并判断假币轻还是重,不是计算算法称真假币
这道题我们可以枚举从A开始逐个假设是假币并假设轻、重,即如下图,对于A-L,分别假设轻、重并调用函数进行判断此时这种情况是否成立
如果假币轻,则应该出现在高的那一边,重,则出现在低的那一边,且天平平衡时肯定没有出现假币,每次枚举时都进行判断,如果结果正确则说明假设正确,这枚币为假币并且轻重也是假设正确
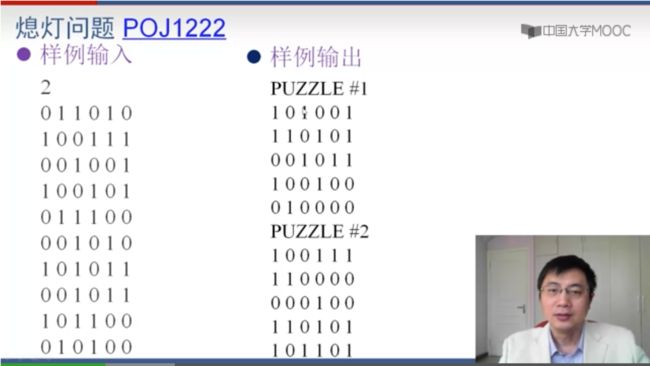
3、熄灯问题
输出的是开关按动的方案,并且注意一个开关按一次是开,按两次就是关相当于没按,所以开关值为0和1,不存在其他次数
而且开关次序也没关系,先按哪个再按哪个结果是一样的
一个简单的想法就是枚举所有开关的可能取值,即每个开关两个值0和1,状态数即2的30次方,超时,需要一种优化的方案
不对全部开关进行枚举,而是选择一部分,例如第一行的状态2的6次方确定后,想要改变第一行的状态只能改变第二行,第二行也就确定了,以此类推,那么后面也就确定,所以只需要遍历第一行的灯
优化算法:
输入存储:只需要一个一维的char类型数据,一个char为8位,一行只需要6位即可,一行6个比特,即5行5个char,使用位运算来进行
用二进制数进行枚举:对于第一行的枚举可以优化为,对于2的次方的枚举,可以用int来累加从0开始到2的k次方减1,即k位01的组合,即2的k次方减1种,例如00,01,10,11->0,1,2,3,用二进制数进行枚举