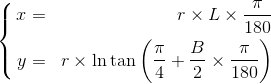瓦片地图面面观之投影
投影
对于地图制图:原面为地球的旋转椭球面,是三维的;承受面(对瓦片地图而言为瓦片)为二维平面的。如何在原面与承受面之间建立点、线、面的一一对应关系是地图制图的必须过程,这一过程通常称之为:地图投影。
目前地图投影方法通常采用数学分析法,也即:在原面和承受面之间建立点与点的函数关系。地球面上的点用地理坐标经纬度(L,B)来确定,平面上的点一般多用平面直角坐标系(x,y)确定。投影即建立函数关系:
式中![]() ,
,![]() 是单值而连续的函数,当地球面上的点连续移动时,平面上的对应点也同时连续移动。
是单值而连续的函数,当地球面上的点连续移动时,平面上的对应点也同时连续移动。
投影方法很多,按投影变形性质分:
- 等角投影:投影承受面上任意两方向线夹角同地球面相应夹角;
- 等面积投影:投影承受面上的有限面积与地球面上相应面积相等;
- 任意投影:即不等角又不等面积的投影,包括等距投影。
按正轴投影经纬网形状分:
- 方位投影:纬线投影为同心圆,经线投影为同心圆的直径,两经线间夹角与相应经差相等;
- 圆柱投影:纬线投影为平行线,经线投影为与纬线垂直而且间隔相等的平行线;
- 圆锥投影:纬线投影为同心圆弧,经线投影为同心圆半径,两经线间夹角与相应经差成正比;
- 还有多圆锥投影、伪方位投影、伪圆柱投影、伪圆锥投影,不再一一介绍。
按投影面与地球面位置关系分:
- 正轴投影:正轴方位投影,投影面与地轴垂直;正轴圆柱和正轴圆锥投影,圆柱轴或圆锥轴与地轴重合;
- 横轴投影:横轴方位投影,投影平面与地球赤道一直径垂直;横轴圆柱或横轴圆锥投影,圆柱轴或圆锥轴同赤道一直径重合;
- 斜轴投影:斜轴方位投影,投影平面与地轴和赤道直径以外的任意大圆直径垂直;斜轴圆柱或斜轴圆锥投影,圆柱轴或圆锥轴与地轴和赤道直径以外的任意大圆直径重合。
投影是个大课题,专业程度要求高,推荐孙达、蒲英霞老师的《地图投影》。对于瓦片地图而言,由于要覆盖整个世界范围且要保证制图美观,能选择的投影方法并不多,因此瓦片地图的投影部分要简化很多。目前主流瓦片地图一般采用Web墨卡托投影、经纬度直投及百度地图独有的百度墨卡托投影。
Web墨卡托投影
Web墨卡托投影方法由谷歌提出,并最先应用于谷歌地图。说起web墨卡托投影,就不得不先说说墨卡托投影。
墨卡托投影由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切于地球,按等角条件将经纬网投影到圆柱面上,将圆柱面展为平面后,即为墨卡托投影。
为了更好地理解墨卡托投影,上图如图1:
图1 墨卡托投影示例
对于墨卡托投影,可以想象为地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假设地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅标准纬线为零度(即赤道)的“墨卡托投影”绘制出的世界地图。
墨卡托投影为等角正轴圆柱投影,由于该投影具有等角性质、经纬网构成简单和等角航线投影为直线的有限,至今仍广泛应用于航海和航空领域。它的缺点也非常明显:面积畸变,而且越往地球南北两级面积畸变越大。从上图中可见格陵兰岛与非洲的面积差不多大小,事实上格陵兰岛面积仅为非洲面积的1/14。
但由于墨卡托投影能满足全世界范围内投影,等角性质能保证地物形状不会被改变,且面积畸变大的两级地区也非人类生产生活集中区域,瓦片地图的先行者谷歌依然选择了墨卡托投影作为谷歌地图的投影方法。
不过为了投影计算简单,降低二次开发难度,谷歌对墨卡托投影做了简化:将地球视为球体而非椭球体。为了区分,通常将谷歌简化后的墨卡托投影称为:Web墨卡托投影(亦称:球面墨卡托投影)。
Web墨卡托投影将地球当做球体而非椭球体,在数学意义上并非一种严密的投影方法。正因为如此,在Web墨卡托投影刚被推出时并不被业界所认可,EPSG也只是戏谑性地给了它一个非正式编号900913(挺有趣的编号,跟google是不是很像)。
但采用Web墨卡托投影的谷歌一经推出,后续的瓦片地图,如:国内的高德地图、腾讯地图、超图、360地图、搜狗地图等, 国外的ArcGIS online、MapQuest、BingMaps等纷纷采用该投影方法。Web墨卡托投影已成为瓦片地图事实上的投影标准,后来EPSG也顺势而为为它赋予了正式编号3857。
Web墨卡托投影面坐标系
Web墨卡托投影面展开后,以赤道作为标准纬线,本初子午线作为中央经线,两者交点为坐标原点,向东向北为正,向西向南为负建立投影面直角坐标系,单位为米。
X轴取值范围:赤道半径r取为6378137.0,则赤道周长为2*π*r = 2*20037508.3427890167,因此X轴的取值范围:[-20037508.3427890167,20037508.3427890167]。
Y轴取值范围:由墨卡托投影方法可知,当纬度接近两极即±90°时,Y值趋向于无穷,无法明确Y轴取值范围。为了解决这个为题,也为了瓦片切片方便,谷歌工程师们把Y轴取值范围也限定在[-20037508.3427890167,20037508.3427890167],如此既能明确Y轴取值范围,也能保证第0级瓦片为正方形,方便各级瓦片切片。
在确定投影面坐标系X/Y轴取值范围后,反算易知对应地理坐标系经度取值范围[-180, 180],纬度取值范围[-85.05112877980659, 85.05112877980659]。
你一定发现了墨卡托投影并未覆盖全球范围,不过没关系企鹅和北极熊们并不在乎。
如下,给出Web墨卡托投影公式:
其中r为地球球体半径,取值为6378137.0m;L为经度,单位为°;L为纬度,单位为°。
经纬度直投
经纬度直投可以说是一种最简单的投影方法,看看投影公式就知道了。
经纬度直投的特点是:经纬网在投影平面上按等间距依次排开,没有复杂的数学变换(简直是码农的福音)。
但经纬度直投属于任意投影,既不等角也不等面积。在低纬度地区长度、角度、面积、形状变化比较小,但越往高纬度,水平长度畸变越严重,很小的纬圈都变得和赤道一样长。受此影响,高纬度地区地物要素变形较为严重,十字路口变成了X型路口,矩形变成了上宽下窄的倒梯形。
上两张来自迈高图的截图,如图2、图3(截图地点位于哈尔滨城区某地)。直观感受下经纬度直投在高纬度地区的畸变。
图2 墨卡托投影下的十字路口
图3 经纬度直投下的十字路口
两张截图均来自同一地点,可见墨卡托投影下的标准十字路口,在经纬直投下变成了X型路口。饶是如此,仍然有瓦片地图采用经纬度直投作为制图投影方法,如:天地图,谷歌地球(二维)。
百度墨卡托投影
百度地图采用自家独有投影方法,其核心还是墨卡托投影,具有等角特性。
但它的投影计算方法与Web墨卡托投影公式不同 ,具体可参见百度地图Js API V1.3。这就导致了百度地图的投影与Web墨卡托投影有一定的误差(投影平面坐标系原点与Web墨卡托投影平面原点不重合,而且每个地区不重合偏移都不同),所以百度地图的投影计算只能通过抽取、转译Js API V1.3的相关代码来实现。可参考以下Qt代码。
/*h file*/
#include
class BaiduMercatorProj
{
public:
BaiduMercatorProj();
~BaiduMercatorProj();
QPoint convertLL2MC(const QPoint& gcp);
QPoint convertMC2LL(const QPoint& pcp);
private:
QPoint convertor(const QPoint& cM, const double cN[10]);
double getRange(double val, double minVal, double maxVal);
double getLoop(double val, double minVal, double maxVal);
private:
const double MCBAND[6] = { 12890594.86, 8362377.87, 5591021, 3481989.83,1678043.12, 0 };
const double LLBAND[6] = { 75, 60, 45, 30, 15, 0 };
const double MC2LL[6][10] = {
{1.410526172116255e-8, 0.00000898305509648872,
-1.9939833816331, 200.9824383106796,
-187.2403703815547, 91.6087516669843,
-23.38765649603339, 2.57121317296198,
-0.03801003308653, 17337981.2
},
{-7.435856389565537e-9, 0.000008983055097726239,
-0.78625201886289, 96.32687599759846,
-1.85204757529826, -59.36935905485877,
47.40033549296737, -16.50741931063887,
2.28786674699375, 10260144.86
},
{-3.030883460898826e-8, 0.00000898305509983578,
0.30071316287616, 59.74293618442277,
7.357984074871, -25.38371002664745,
13.45380521110908, -3.29883767235584,
0.32710905363475, 6856817.37
},
{-1.981981304930552e-8, 0.000008983055099779535,
0.03278182852591, 40.31678527705744,
0.65659298677277, -4.44255534477492,
0.85341911805263, 0.12923347998204,
-0.04625736007561, 4482777.06
},
{3.09191371068437e-9, 0.000008983055096812155,
0.00006995724062, 23.10934304144901,
-0.00023663490511, -0.6321817810242,
-0.00663494467273, 0.03430082397953,
-0.00466043876332, 2555164.4
},
{2.890871144776878e-9, 0.000008983055095805407,
-3.068298e-8, 7.47137025468032,
-0.00000353937994, -0.02145144861037,
-0.00001234426596, 0.00010322952773,
-0.00000323890364, 826088.5}
};
const double LL2MC[6][10] = {
{-0.0015702102444, 111320.7020616939,
1704480524535203, -10338987376042340,
26112667856603880, -35149669176653700,
26595700718403920, -10725012454188240,
1800819912950474, 82.5
},
{0.0008277824516172526, 111320.7020463578,
647795574.6671607, -4082003173.641316,
10774905663.51142, -15171875531.51559,
12053065338.62167, -5124939663.577472,
913311935.9512032, 67.5
},
{0.00337398766765, 111320.7020202162,
4481351.045890365, -23393751.19931662,
79682215.47186455, -115964993.2797253,
97236711.15602145, -43661946.33752821,
8477230.501135234, 52.5
},
{0.00220636496208, 111320.7020209128,
51751.86112841131, 3796837.749470245,
992013.7397791013, -1221952.21711287,
1340652.697009075, -620943.6990984312,
144416.9293806241, 37.5
},
{-0.0003441963504368392, 111320.7020576856,
278.2353980772752, 2485758.690035394,
6070.750963243378, 54821.18345352118,
9540.606633304236, -2710.55326746645,
1405.483844121726, 22.5
},
{-0.0003218135878613132, 111320.7020701615,
0.00369383431289, 823725.6402795718,
0.46104986909093, 2351.343141331292,
1.58060784298199, 8.77738589078284,
0.37238884252424, 7.45
}
};
}; /*cpp file*/
#include "BaiduMercatorProj.h"
BaiduMercatorProj::BaiduMercatorProj()
{
}
BaiduMercatorProj::~BaiduMercatorProj()
{
}
QPoint BaiduMercatorProj::convertLL2MC(const QPoint& pt)
{
double cN[10];
QPoint cL(getLoop(pt.x(), -180, 180), getRange(pt.y(), -74, 74));
const staitc int len = 6;//sizeof LLBAND / sizeof(double);
int cNok = false;
for (int i = 0; i < len; i++)
{
if (cL.y() >= LLBAND[i])
{
memcpy_s(cN, 80, LL2MC[i], 80);
cNok = true;
break;
}
}
if (!cNok) {
for (int i = len - 1; i >= 0; i--)
{
if (cL.y() <= -LLBAND[i]) {
memcpy_s(cN, 80, LL2MC[i], 80);
break;
}
}
}
return convertor(pt, cN);
}
QPoint BaiduMercatorProj::convertMC2LL(const QPoint& pt)
{
double cO[10];
QPoint cM(fabs(pt.x()), fabs(pt.y()));
const static int len = 6;// sizeof MCBAND / sizeof(double);
for (int i = 0; i < len; i++)
{
if (cM.y() >= MCBAND[i])
{
memcpy_s(cO, 80, MC2LL[i], 80);
break;
}
}
return convertor(pt, cO);
}
Point BaiduMercatorProj::convertor(const Point& cM, const double cN[10])
{
double T = cN[0] + cN[1] * fabs(cM.x());
double cL = fabs(cM.y()) / cN[9];
double cO = cN[2] + cN[3] * cL + cN[4] * cL * cL + cN[5] * cL *
cL * cL + cN[6] * cL * cL * cL * cL + cN[7] * cL *
cL * cL * cL * cL + cN[8] * cL * cL * cL * cL *
cL * cL;
T *= (cM.x() < 0 ? -1 : 1);
cO *= (cM.y() < 0 ? -1 : 1);
return Point(T, cO);
}
double BaiduMercatorProj::getLoop(double val, double minVal, double maxVal)
{
double loopVal = 0.0;
while (val > maxVal) {
loopVal -= maxVal - minVal;
}
while (val < minVal) {
loopVal += maxVal - minVal;
}
return loopVal;
}
double BaiduMercatorProj::getRange(double val, double minVal, double maxVal)
{
double rangeVal = 0.0;
rangeVal = max(val, minVal);
rangeVal = min(val, maxVal);
return rangeVal;
}
主流瓦片地图的投影汇总
主流瓦片地图的地理坐标系可分以下几类:
| 投影 | ||
| 1 | Web墨卡托投影 | 谷歌地图、高德地图、腾讯地图、搜狗地图、必应地图、OpenStreetMap、ArcGIS online、MapQuest、超图、360地图 |
| 2 | 经纬度直投 | 谷歌地球、天地图(经纬直投) |
| 3 | 百度墨卡托 | 百度地图 |