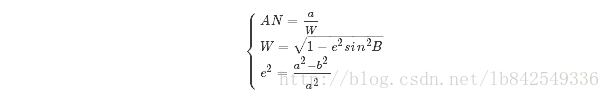坐标转换--基准面转换（布尔莎七参数）

坐标转换–基准面转换（布尔莎七参数）

在坐标转换中，除了正投影和反投影的转换，还有不同基准面之间的转换。基准面的转换有很多种转换模型，常见的有三参数和七参数转换。三参数的转换主要是通过对x,y,z三个坐标轴进行平移操作，使用于小范围的地方坐标基准之间的转换，对精度要求不高。相对于三参数转换，七参数转换在其基础上增加的对x,y,z三个坐标轴的旋转分量以及缩放比例。这里，我们主要对布尔莎七参数模型进行介绍。
我们对一个经纬度坐标进行七参数转换时，一般先将其转为地心坐标系，就是以地心为原点的三维坐标系，再利用空间直角坐标系的转换公式，使用七参数对其进行转换，将转换的结果再转回经纬度坐标，即可完成椭球基准的转换。

1. 经纬度坐标转地心空间直角坐标

转换公式：

其中：

代码如下：

/**
 * 将地理坐标系转为空间直角坐标系
 * 
 * @param coord
 * @param srcCS
 * @param pointCS
 * @return
 */
public Coordinate transFromGeoToXYZ(Coordinate coord, GeoCoordinateSystem CS) {
    Coordinate newCoord = new Coordinate();

    // 将地理坐标系转为空间直角坐标系
    double srcB = Math.toRadians(coord.X);
    double srcL = Math.toRadians(coord.Y);
    double srcH = coord.Z;

    // 椭球长半轴
    double a = CS.referenceSpheroid.semimajorAxis;
    // 椭球第一偏心率
    double e = CS.referenceSpheroid.getFirstEccentricity();
    double W = Math.sqrt(1 - e * e * Math.sin(srcB) * Math.sin(srcB));
    // 卯酉圈曲率半径
    double N = a / W;

    // 使用地理坐标转空间直角坐标公式
    newCoord.X = (N + srcH) * Math.cos(srcB) * Math.cos(srcL);
    newCoord.Y = (N + srcH) * Math.cos(srcB) * Math.sin(srcL);
    newCoord.Z = (N * (1 - e * e) + srcH) * Math.sin(srcB);

    return newCoord;
}

2. 基准转换

七参数基准转换的原理同三维坐标系之间的坐标转换原理类似，这里给出公式如下：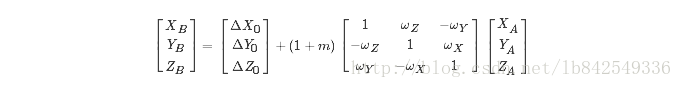

其中，ΔX，ΔY，ΔZ为平移分量，m为缩放系数，ω为旋转矩阵
代码如下：

/**
 * 七参数基准转换
 * 
 * @param coord
 * @param srcCS
 * @param pointCS
 * @return
 */
private Coordinate transformBySevenparam(Coordinate coord, GeoCoordinateSystem srcCS, GeoCoordinateSystem pointCS) {
    // 无七参数默认为同一参考椭球体
    if (sevenParma == null) {
        return coord;
    }

    Coordinate newCoord = new Coordinate();

    // 将地理坐标系转为空间直角坐标系
    Coordinate tmpCoord = transFromGeoToXYZ(coord, srcCS);

    double x = sevenParma[0] + (tmpCoord.X + sevenParma[5] * tmpCoord.Y - sevenParma[4] * tmpCoord.Z) * (1 + sevenParma[6]);
    double y = sevenParma[1] + (-sevenParma[5] * tmpCoord.X + tmpCoord.Y + sevenParma[3] * tmpCoord.Z) * (1 + sevenParma[6]);
    double z = sevenParma[2] + (sevenParma[4] * tmpCoord.X - sevenParma[3] * tmpCoord.Y + tmpCoord.Z) * (1 + sevenParma[6]);
    Coordinate tmpCoord1 = new Coordinate(x, y, z);

    // 将转换后的空间直角坐标转换为地理坐标
    newCoord = transFromXYZToGeo(tmpCoord1, pointCS);
    return newCoord;
}

3. 地心空间直角坐标转经纬度

最后一步就是将基准转换之后的地心空间直角坐标转回经纬度坐标，公式如下：

观察公式，这里由于N的计算跟B相关，因此该公式需要通过迭代的方式来求经纬度。可以设迭代初值为：

代码如下：

/**
 * 将空间直角坐标系转为地理坐标系
 * 
 * @param coord
 * @param srcCS
 * @param pointCS
 * @return
 */
public Coordinate transFromXYZToGeo(Coordinate coord, GeoCoordinateSystem CS) {
    Coordinate newCoord = new Coordinate();

    double X = coord.X;
    double Y = coord.Y;
    double Z = coord.Z;

    // ------------------------------直接算法-------------------------------//
    /*
     // 椭球长半轴 
     double a = CS.referenceSpheroid.SemimajorAxis; 
     double b = CS.referenceSpheroid.SemiminorAxis;

     // 计算中间参数 
     double N, W, sb; 
     double e2 = CS.referenceSpheroid.GetFirstEccentricityPow2(); 
     double ee = CS.referenceSpheroid.GetSecondEccentricityPow2(); 
     double r = Math.sqrt(X*X + Y*Y); 
     double alpha = Math.atan(Z*a/(r*b)); 
     double cosal = Math.cos(alpha);
     double sinal = Math.sin(alpha);

     // 计算结果 
     double L = Math.atan(Y/X) + Math.PI; 
     double B = Math.atan((Z+ee*b*sinal*sinal*sinal)/(r-e2*a*cosal*cosal*cosal));

     sb = Math.sin(B); 
     W = Math.sqrt(1 - e2*sb*sb); 
     N = a / W; 
     double H = r/Math.cos(B) - N;
     */
    // ------------------------------直接算法end-------------------------------//

    // ------------------------------迭代算法-------------------------------//
    double a, N, W, e2, r2, sb;
    double B1, B0, H1, H0, B, L, H;

    a = CS.referenceSpheroid.semimajorAxis;
    e2 = CS.referenceSpheroid.getFirstEccentricityPow2();
    r2 = X * X + Y * Y;

    L = Math.atan(Y / X) + Math.PI;
    B0 = Math.atan(Z / Math.sqrt(r2));
    sb = Math.sin(B0);
    W = Math.sqrt(1 - e2 * sb * sb);
    N = a / W;
    H0 = Z / sb - N * (1 - e2);

    // 最大迭代次数
    int maxIter = 30;
    // 迭代计数
    int iter = 0;

    while (true) {
        iter++;
        B1 = Math.atan2(Z * (N + H0), Math.sqrt(r2) * (N * (1 - e2) + H0));
        sb = Math.sin(B1);
        W = Math.sqrt(1 - e2 * sb * sb);
        N = a / W;
        H1 = Z / sb - N * (1 - e2);
        if ((Math.abs(B1 - B0) < Math.pow(10, -15) && Math.abs(H1 - H0) < Math.pow(10, -8)) || iter > maxIter) {
            break;
        }
        B0 = B1;
        H0 = H1;
    }

    B = B1;
    H = H1;
    // ------------------------------迭代算法end-------------------------------//

    newCoord.X = Math.toDegrees(B);
    newCoord.Y = Math.toDegrees(L);
    newCoord.Z = H;

    return newCoord;
}

4. 七参数反解

到这里可能会有童鞋会问，那我如果没有七参数要怎么办，答案是七参数是可以反解出来的，七参数的反解需要三组以上的已知点，以布尔莎七参数模型为基础，利用已知的三组或三组以上的点，通过最小二乘法就可以反解出布尔莎模型中的参数，也就是我们需要的七参数。
这里我们首先把布尔莎七参数的公式写为如下的形式：

转换成方程式组，即：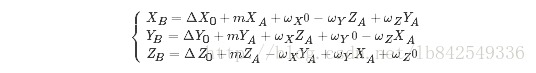

上面这种形式想必大家都比较熟悉，式中有七个未知量，如果有三组已知点，则按照上述形式可以构建9组方程，即可利用最小二乘法求得七个参数的值。
下面给出计算代码：

/**
 * 根据公共点进行七参数反解(布尔莎模型)
 * 
 * @param srcBL
 * @param tagBL
 * @return
 */
public double[][] calculateSevenParamBrusa(Coordinate[] srcBL, Coordinate[] tagBL) {
    if (srcBL.length != tagBL.length) {
        return null;
    }

    int n = srcBL.length;
    double[][] Q = new double[n * 3][7];
    double[][] l = new double[n * 3][1];

    for (int i = 0; i < n; i++) {
        Coordinate tmp1 = transFromGeoToXYZ(srcBL[i], (GeoCoordinateSystem) srcCoordinateSystem);
        Coordinate tmp2 = transFromGeoToXYZ(tagBL[i], (GeoCoordinateSystem) pointCoordinateSystem);

        // 构建参数矩阵
        Q[i * 3][0] = 1;
        Q[i * 3 + 1][0] = 0;
        Q[i * 3 + 2][0] = 0;
        Q[i * 3][1] = 0;
        Q[i * 3 + 1][1] = 1;
        Q[i * 3 + 2][1] = 0;
        Q[i * 3][2] = 0;
        Q[i * 3 + 1][2] = 0;
        Q[i * 3 + 2][2] = 1;
        Q[i * 3][3] = 0;
        Q[i * 3 + 1][3] = tmp1.Z;
        Q[i * 3 + 2][3] = -1 * tmp1.Y;
        Q[i * 3][4] = -1 * tmp1.Z;
        Q[i * 3 + 1][4] = 0;
        Q[i * 3 + 2][4] = tmp1.X;
        Q[i * 3][5] = tmp1.Y;
        Q[i * 3 + 1][5] = -1 * tmp1.X;
        Q[i * 3 + 2][5] = 0;
        Q[i * 3][6] = tmp1.X;
        Q[i * 3 + 1][6] = tmp1.Y;
        Q[i * 3 + 2][6] = tmp1.Z;

        l[i * 3][0] = tmp2.X - tmp1.X;
        l[i * 3 + 1][0] = tmp2.Y - tmp1.Y;
        l[i * 3 + 2][0] = tmp2.Z - tmp1.Z;
    }

    // 最小二乘法求解
    Matrix matQ = new Matrix(Q);
    Matrix matl = new Matrix(l);
    double[][] X = matQ.solve(matl).getArrayCopy();

    // 将旋转角度结果转为秒
    X[3][0] = Math.toDegrees(X[3][0]) * 3600;
    X[4][0] = Math.toDegrees(X[4][0]) * 3600;
    X[5][0] = Math.toDegrees(X[5][0]) * 3600;
    return X;
}

上面求最小二乘解使用了外部库jama，有兴趣的童鞋可以自己封装一个矩阵运算的类来调用，总之目的都是一样：解出七参数。
以上代码在细节等处理上还可以继续优化，这里只是给出重点的计算过程。如有错误，请指正，共同学习！