移动互联网的入口-二维码(二维码生成原理及流程)
目录
1 引入
2 历史
2.1 一维码
2.2 二维码
3 分类
3.1 线性堆叠式二维码
3.2 矩阵式二维码
3.3 邮政码
4 QR code二维码结构
5 QR code二维码生成流程及原理
5.1 数据编码
5.2 纠错码
5.3 最终编码
5.4 画二维码
5.5 二维码优势
6 个性二维码
7 总结
1 引入
近年来,随着移动互联网的发展,二维码也开始被广泛应用,尤其是其与电子商务的紧密结合,使二维码成为一个当下很火的概念。随着国家信息化进程的不断推进,物联网应用发展的高歌猛进,我国二维码行业也呈现出百家争鸣的趋势,涉足二维码应用的商家越来越多,可谓是万“码”奔腾。
2 历史
首先我们简单了解下二维码的发展历史。
2.1 一维码
谈到二维码就不得不涉及一维码,上个世界 60 年代至 70 年代,条形码联合发明人诺曼・约瑟夫・伍德兰德(Norman Joseph Woodland)发明了一维码(条形码),该技术的诞生几乎改变了全球的商业活动形式,使得收银员的工作效率变得更高效,顾客也可以节省更多时间。不过初代的条形码采用的还是还是环形设计,想要完成扫描还需要格外安装一部 500 瓦特发光体的巨型扫描仪吗,非常厚重但是节省了不少的劳动力。
2.2 二维码
根据市场的需求一维码(条形码)用的越来越多,但是其缺点也展现出来。我们生活中使用过的一维码场景最多的就是商品扫码或者快递码,为什么会在这些场景下呢,因为只有这些需求是一串字母或数字。所以一维码的数据容量较小(30 个字符左右)、只能包含字母和数字、尺寸相对较大(空间利用率较低)、遭到损坏后便不能阅读的缺点暴露出来。为了弥补这些缺陷,这个时候人们开始寻找更佳的代替方案。
1994 年,日本电装公司正式宣布公开首个 QR Code,而 QR 的全称就是“Quick Response”,翻译过来就是快速响应,二维码相比一维码(条形码)确实具有数据容量更大、超越了字母数字的限制、尺寸小、具有抗损毁能力等优势,逐渐的中国物品编码中心根据市场需要制定了两个二维码的国家标准,2016年8月3日,支付清算协会向支付机构下发《条码支付业务规范》,中国的移动支付如支付宝、微信等应用场景遍地开花。
3 分类
二维条码/二维码(2-dimensional bar code)是用某种特定的几何图形按一定规律在平面(二维方向上)分布的、黑白相间的、记录数据符号信息的图形,主要有三类分别是线性堆叠式二维码、矩阵式二维码、邮政码。
3.1 线性堆叠式二维码
是在一维条码编码原理的基础上,将多个一维码在纵向堆叠而产生的。典型的码制如:Code16K、Code 49、PDF417等。
3.2 矩阵式二维码
是在一个矩形空间通过黑、白像素在矩阵中的不同分布进行编码。典型的码制如:Aztec、Maxi、Code、QRCode(也是此次文章分享内容)、Data、Matrix等。
3.3 邮政码
通过不同长度的条进行编码,主要用于邮件编码,如:Postnet 、 BPO4-State 。
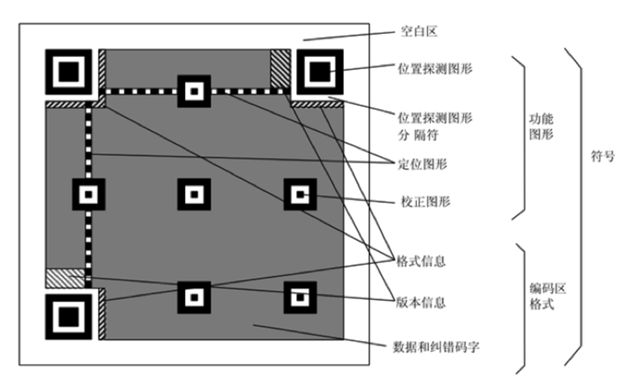
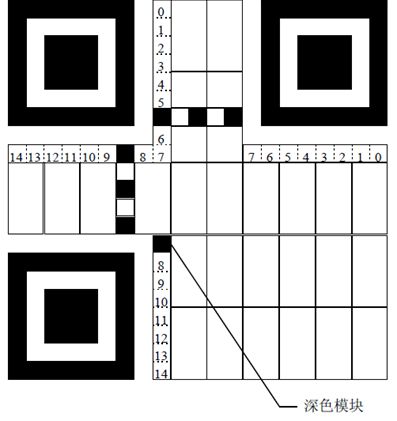
4 QR code二维码结构
知道了二维码由来和分类,我们就逐渐去看看到底是怎么生成的,这里选择了市场上流行的、又有丰富的参考文档的QR code二维码。
QR code二维码整体分为功能区和编码区,功能区主要用于定位,编码区则是真正存储数据的。
有两个地方需要注意:
- 一是二维码所有的模块中,储存的并不都是我们需要的信息,甚至只有一小部分才是。在上面的图中,只有数据和纠错码字中的数据才是我们实际想存储的数据。
- 二是版本信息:二维码一共有40个版本,不同版本的区别主要是存储数据的模块的多少(每一块黑/白块就是一个模块),模块数量遵循: moduleCount = 21 + (n-1)×4,比如:版本1的模块数量是21*21,版本40的模块数量为: 21 + (40-1)×4 = 177。
那么这些块都代表什么意思呢?其中功能图形包括位置探测图形、位置探测分隔符、定位图形、校正图形四大块,编码区包括格式信息、版本信息、数据和纠错码字三大块。具体定义如下:
【位置探测图形】三个就可以标识一个矩形了
【位置探测分隔符】每个探测图形和编码区域之间有一条1单位宽度的分隔符.由白色块组成
二维码有40种尺寸,尺寸过大了后需要有根标准线,不然扫描的时候可能会扫歪了
【定位图形】黑白色相间交替组成的一行一列两条位于横纵的两两探测图形之间,用于确定符号的密度和版本,提供决定模块坐标的基准位置
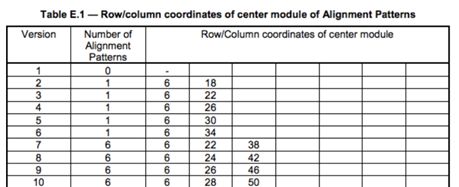
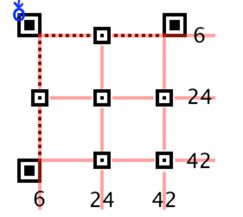
【校正图形】类似小号的探测图形,中心矩形边框变为1单位,这种校正图形的数量由version来定,大于version 1的都有该校正图形.
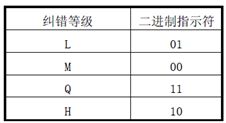
【格式信息】表示该二维码的纠错级别,分为L、M、Q、H;
【版本信息】即二维码的规格,QR码符号共有40种规格的矩阵(一般为黑白色),从21x21(版本1),到177x177(版本40),每一版本符号比前一版本 每边增加4个模块。
【数据和纠错码字】使用黑白的二进制网格编码内容。8个格子可以编码一个字节。数据是我们需要的信息,纠错码字用于修正二维码损坏带来的错误。
5 QR code二维码生成流程及原理
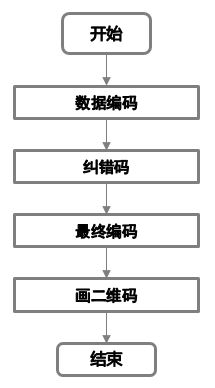
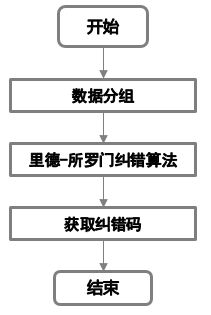
二维码生成流程主要分为四步,首先我们将所需要展示的数据进行数据编码,其次对于数据编码后的数据码利用里德-所罗门算法计算其纠错码,然后将数据码和纠错码合并到一起形成的就是最终编码,最后利用二维码结构进行画二维码流程,即先对功能图形进行放置,在对格式、版本信息、数据进行放置,最后对于得到的二维码进行掩码计算获取最终可以投入使用的二维码。大体流程如下图:
接下来就依照上面的流程进行详细的介绍。
5.1 数据编码
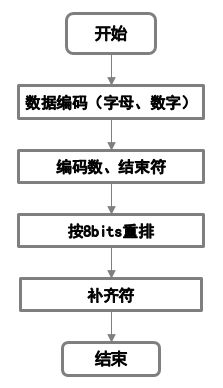
这里的数据编码指的是对于二维码中所需要展示的数据进行编码,为了得到一串0和1形成的数据填入我们的二维码格子,其编码过程如下流程图所示。首先对所要展示的数据进行数据编码,然后根据编码数添加结束符,最后利用得到的数据串进行按8bits重排,最后根据纠错等级添加补齐符得到我们需要的数据码。
5.1.1 数据编码
数据编码顾名思义就是对于我们所需要展示的数据进行编码,分为数字编码(Numeric mode)、字符编码(Alphanumeric mode)、字节编码(Byte mode)、日文编码(Kanji mode)等等。本章节主要为大家介绍数据编码(Numeric mode)、字符编码(Alphanumeric mode)两种常用编码方式。
数字编码
数字编码(Numeric mode)包含从0到9。如果需要编码的数字的个数不是3的倍数,那么,最后剩下的1或2位数会被转成4或7bits,则其它的每3位数字会被编成 10,12,14bits,编成多长还要看二维码的尺寸(下面有一个表Table 3说明了这点)
具体实现我们来看这个例子:
在Version 1的尺寸下,纠错级别为H的情况下,编码: 01234567
- 把上述数字分成三组: 012 345 67
- 把他们转成二进制: 012 转成 0000001100; 345 转成 0101011001; 67 转成 1000011。
- 把这三个二进制串起来: 0000001100 0101011001 1000011
- 把数字的个数转成二进制 (version 1-H是10 bits ): 8个数字的二进制是 0000001000
- 把数字编码的标志0001和第4步的编码加到前面: 0001 0000001000 0000001100 0101011001 1000011
注意:
- 这里的三位数字被转成10位的原因是由于根据table3中版本 1 所对应的数字编码位数。
- 数字编码的标志如下图所示,数字编码为0001,字符编码为0010。
字符编码
字符编码(Alphanumeric mode)包括0-9,大写的A到Z(没有小写),以及符号$ % * + – . / : 包括空格。这些字符会映射成一个字符索引表。如下所示:(其中的SP是空格,Char是字符,Value是其索引值)编码的过程是把字符两两分组,然后转成下表的45进制,然后转成11bits的二进制,如果最后有一个落单的,那就转成6bits的二进制。
在Version 1的尺寸下,纠错级别为H的情况下,编码: AC-42
-
从字符索引表中找到 AC-42 这五个字条的索引 (10,12,41,4,2)
-
两两分组: (10,12) (41,4) (2)
-
把每一组转成11bits的二进制:
(10,12) 的45进制为 10 * 45+12,等于 462 转成 00111001110
(41,4) 的45进制为41 * 45+4, 等于 1849 转成 11100111001
(2) 等于 2 转成 000010
-
把这些二进制连接起来:00111001110 11100111001 000010
-
把字符的个数转成二进制 (Version 1-H为9 bits ): 5个字符,5转成 000000101
-
在头上加上编码标识 0010 和第5步的个数编码: 0010 000000101 00111001110 11100111001 000010
注意:
- 第5步中 (Version 1-H为9 bits ) 这个依据table3中Version 1所对应的字符编码位数。
- 第6步中编码标识 0010如下图所示,数字编码为0001,字符编码为0010。
5.1.2 结束符
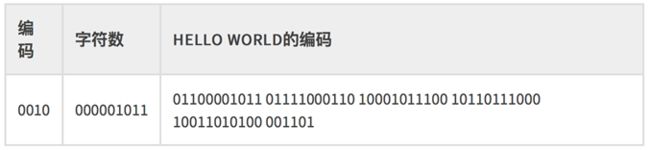
假如我们有个HELLO WORLD的字符串要编码,根据字符编码结果,我们可以得到下面的编码
加上结束符:
5.1.3 按8bits重排
如果所有的编码加起来不是8个倍数我们还要在后面加上足够的0,比如上面一共有78个bits,所以,我们还要加上2个0,然后按8个bits分好组:
5.1.4 补齐码
由于关于每一个Version的每一种纠错级别的最大Bits限制,所以如果还没有达到我们最大的bits数的限制,我们还要加一些补齐码(Padding Bytes),Padding Bytes就是重复下面的两个bytes:11101100 00010001 。
假设我们需要编码的是Version 1的Q纠错级,那么,其最大需要104个bits,而我们上面只有80个bits,所以,还需要补24个bits,也就是需要3个Padding Bytes,我们就添加三个,于是得到下面的编码:
5.2 纠错码
纠错码目的是如果我们的数据依据所罗门算法进行处理得到与数据码相对应的纠错码,上面我们提到了纠错级别,二维码中有四种级别的纠错(从低到高为L、M、Q、H),这就是为什么有人在二维码的中心位置加入图标,也依旧能够扫描(就是二维码残缺量不超过所对应的纠错等级能允许的范围时,使用扫描工具依旧能扫描出内容的原因)。
其具体流程为对于我们所要展示的数据进行分组,按组在进行分块,根据得到的数据块依次进行(Reed-Solomon error correction) 里德-所罗门纠错算法处理,最后每个块都得到了相应的纠错码。相应流程图如下所示。
5.2.1 数据分组
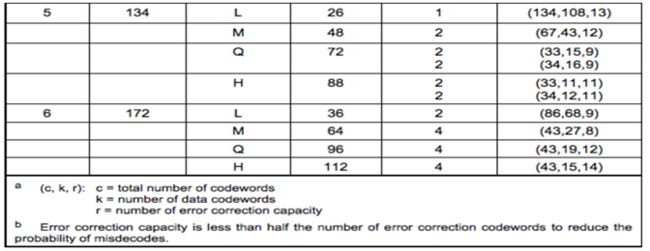
我们需要对数据码进行分组,也就是分成不同的Block,然后对各个Block进行纠错编码,对于如何分组,我们可以查看定义表。
注意:
- Number of Error Code Correction Blocks :需要分多少个块。
- Error Correction Code Per Blocks:每一个块中的code个数,所谓的code的个数,也就是有多少个8bits的字节。
- 上图左侧依次是版本号、纠错等级、需要的组和blocks,(c、k、r)表示每个组的总数据个数、每个块的数据码个数、每个块的纠错码个数为2*r。
那么具体我们来看一下实例:
上述的Version 5 + Q纠错级:需要4个Blocks(2个Blocks为一组,共两组),头一组的两个Blocks中各15个bits数据 + 各 9个bits的纠错码(注:表中的codewords就是一个8bits的byte)(再注:最后一例中的(c, k, r )的公式为:c = k + 2 * r)
根据上述表中我们可以看出,在Version 5 + Q纠错级时数据需要分为2个组,每个组拥有2个block,每个block拥有15个数据,2*9=18个纠错码。
5.2.2 里德-所罗门纠错算法
事实上,尽管纠错码在数学上似乎令人生畏。但是数学独创性的复杂性也掩盖了它相当直观的目标和机制,这里我们也是可以明白其大概纠错机制的。
纠错码可能看起来像一个挺难的数学概念,但实际上它们是基于一个巧妙的数学实现的直观理念:让我们使数据结构化,以便我们可以在数据损坏时,通过“修复”结构,“猜测”损坏的数据是什么。在数学上,我们使用伽罗瓦域的多项式来实现这个结构,这就是为什么所罗门算法涉及很多多项式计算。
举一个更实用的比喻:
假设您想要将消息传递给其他人,但这些消息可能会一路被破坏。纠错码的主要观点是,我们可以使用一小组仔细选择的单词,即“缩小字典”,而不是使用整个字典词典,以便每个字词与其他字词不同。这样,当我们收到一条消息时,我们只需要在缩小的字典内查找1)检测哪些字被损坏(因为它们不在我们缩小的字典中); 2)通过查找我们词典中最相似的单词来纠正被破坏的单词。
看起来也云里雾里,那么我们再来看下面这个例子:
t h i s
t h a t
c o r n添加一组独特的字符,以便在任何新增位置都没有重复的字符,并添加一个单词来帮助解释:
t h i s a b c d
t h a t b c d e
c o r n c d e f
t h i n d e f g请注意,此字典中的每个单词与其他单词至少有5个字符不同,因此距离为5。这允许在已知位置最多有4个错误,这些错误称为丢失,或者在未知位置中的2个错误需要纠正。
假设发生4次错误:
t * * * a b * d然后可以在字典中搜索4个未丢失的字符,并找到与这4个字符匹配的唯一条目,因为距离为5。
假设在这些模式之一中有两个错误发生:
t h i x a x c d
x h i x a b c d
t h x x a b c d这里的问题是错误的位置是未知的。8个中取6个字符的可能子集有28个,因此使用有这6个字符的28个子集中的每个子集进行搜索,因为距离为5,将只有一个匹配6个字符的子集(假设发生2个或更少的错误)。
通过这些示例,你可以看到数据冗余在恢复丢失信息中的优势:冗余字符可帮助你恢复原始数据。前面的例子显示了粗略的错误纠正方案是如何工作的。Reed-Solomon的核心思想是相似的,将冗余数据附加到基于伽罗华域数学的消息上。原始纠错解码器与上述错误示例类似,搜索与有效消息相对应的接收消息的子集,并选择匹配最多的消息作为纠正的消息。
如果一个单词在通信中被破坏了,这没什么大不了的,因为我们可以通过查看字典并找到最接近的单词来很容易地修复它,这可能是正确的(但是如果输入消息太严重损坏,则有可能选择错误,但概率非常小)。而且,我们的单词越长,它们就越可分离,因为更多的字符可以被破坏而不受任何影响。
所以每个block的纠错码计算主要是通过上述说到的里德-所罗门纠错算法(Reed-Solomon error correction)来实现的。对于这个算法,里面有很多的数学计算涉及到多项式,还有不理解的同学直接认为它就像一种加密算法,把数据码经过一系列神操作变成了另外一堆个数都给你规定好的数据码。
5.2.3 获取纠错码
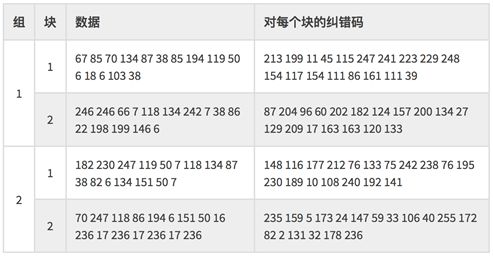
在利用里德 - 所罗门算法得到了各个块的纠错码后,具体数据如下图所示。一个version5-Q的示例(可以看到每一块的纠错码有18个codewords,也就是18个8bits的二进制数)
5.3 最终编码
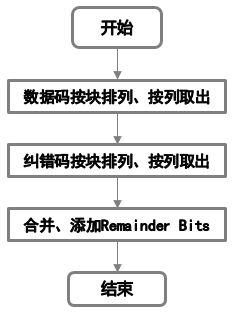
得到纠错码后这个时候如果你以为我们可以开始画图,你就错了。我们要想填进去的数据是得到一串数据,而不是分成好多块,所以这时候就到了要把数据码和纠错码的各个codewords交替放在一起变成一串数据。
其流程如下图所示。将数据码和纠错码分别按块排列,按列取出,然后进行合并,并添加相应的remainder构成最终编码。
流程看起来挺简单的,但是到了具体实例怎么操作呢?
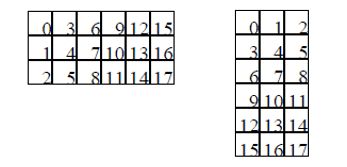
5.3.1 数据码按块排列、按列取出
对于数据码:把每个块的第一个codewords先拿出来按顺度排列好,先取第一组的第一块的第一个,然后再取第一组的第二块的第二个,如此类推。
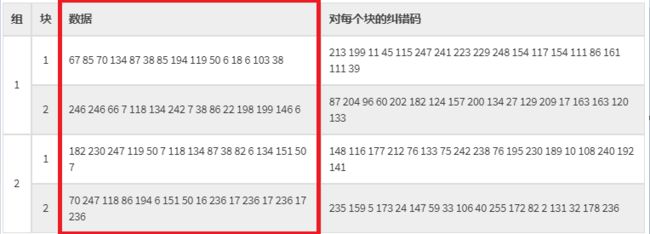
上述示例中的Data Codewords如下:
- 先取块1的第一列:67, 246, 182, 70
- 然后再取块2的第一列:67, 246, 182, 70, 85,246,230 ,247
- 如此类推:67, 246, 182, 70, 85,246,230 ,247 ……… ……… ,38,6,50,17,7,236
5.3.2 纠错码按块排列、按列取出
和数据码取的一样。
如下:
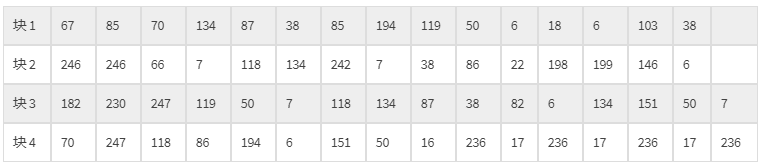
- 先取块1的第一列:213,87,148,235
- 然后再取块2的第一列:213,87,148,235, 199,204,116,159
- 如此类推:213,87,148,235,199,204,116,159,…… …… 39,133,141,236
5.3.3 数据码和纠错码合并
由以上数据码和纠错码分别按块排列、按列取出得到下述结果,
数据码:67, 246, 182, 70, 85,246,230 ,247 ……… ……… ,38,6,50,17,7,236
纠错码:213,87,148,235,199,204,116,159,…… …… 39,133,141,236这两组放在一起(纠错码放在数据码之后)得到:
67, 246, 182, 70, 85, 246, 230, 247, 70, 66, 247, 118, 134, 7, 119, 86, 87, 118, 50, 194, 38, 134, 7, 6, 85, 242, 118, 151, 194, 7, 134, 50, 119, 38, 87, 16, 50, 86, 38, 236, 6, 22, 82, 17, 18, 198, 6, 236, 6, 199, 134, 17, 103, 146, 151, 236, 38, 6, 50, 17, 7, 236, 213, 87, 148, 235, 199, 204, 116, 159, 11, 96, 177, 5, 45, 60, 212, 173, 115, 202, 76, 24, 247, 182, 133, 147, 241, 124, 75, 59, 223, 157, 242, 33, 229, 200, 238, 106, 248, 134, 76, 40, 154, 27, 195, 255, 117, 129, 230, 172, 154, 209, 189, 82, 111, 17, 10, 2, 86, 163, 108, 131, 161, 163, 240, 32, 111, 120, 192, 178, 39, 133, 141, 236这就是我们的数据区,终于获取到整体数据了,开心~
5.3.4 添加补齐符
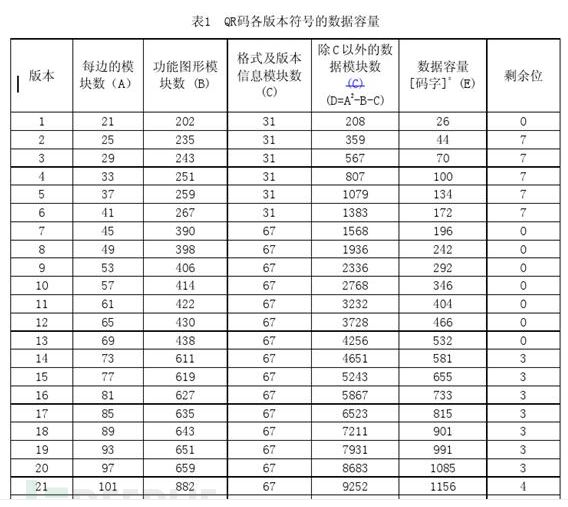
QR 码各版本符号所包含的数据和纠错块通常正好填满符号的码字容量,而在某些版本中,也许需要3、4 或7 个剩余位,添加在最终的信息位流中以正好填满编码区域的模块数,具体参照我们的表1 。
上述的5Q版的二维码,参照定义表还要加上7个bits,所以在最终编码的后面加零就好了。
5.4 画二维码
终于到了万众期待的一步!最终编码有了那么可以画二维码了,画二维码肯定也有流程,二维码结构如上图所示,就像我们第一部分提到的各个位置放置不同的模块,但整体分为功能区和数据区放置。首先需要对功能区放置,其次放置最终编码,最后进行掩码处理。接下来让我们一步步感受一下如何画一个二维码。
5.4.1 位置探测图形
位置探测图画在三个角上,并且大小是固定的,外边宽为7,中间宽位5,内边宽为3 。
5.4.2 位置探测分隔符
在每个位置探测图形和编码区域之间有宽度为1个模块的分隔符。
5.4.3 校正图形
校正图形的数量视符号的版本号而定,大小是固定的,外边宽为5,内边宽为3 。如下表所示如果时v8版本那么就有6个校正图形。
5.4.4 定位图形
定位图形是水平和垂直定位图形,分别为一个模块宽的一行和一列,由深色浅色模块交替组成,其开始和结尾都是深色模块。version8版本时定位图形行和列穿过2个校正图形。
5.4.5 格式信息
格式信息为15位,其中有5个数据位,10个是用BCH(15,5)编码计算得到的纠错位。BCH(15,5)一共15位,数据占5位,纠错码10位。
- 5个数据bits:其中,2个bits用于表示纠错等级, 3个bits表示使用的掩码。
- 10个纠错bits:主要通过BCH Code来计算。
我们来看个例子:
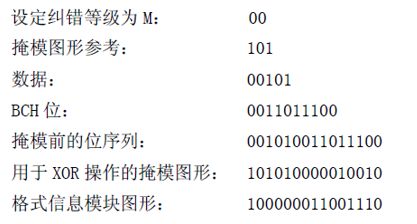
各个数据获取来源为:
掩膜图形参考:8个掩膜图形选第5个,二进制为101 (掩模图形我们在后面介绍)
数据: 纠错等级 + 掩模图形
BCH位: 由BCH Code来计算
掩膜前的位序列:数据 + BCH位
用于XOR操作的掩模图形:掩模图形参考的掩模获取
格式信息模块图形: 与掩模图形做XOR操作。其中XOR操作为如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。(因为我们选用了00的纠错级别和000的Mask,从而造成全部为白色,这会增加我们的扫描器的图像识别的困难,白色越多扫码越困难)下图可以看到15位的格式信息放置了两遍,出现两次以提供冗余,因为它的正确译码对整个符号的译码至关重要。
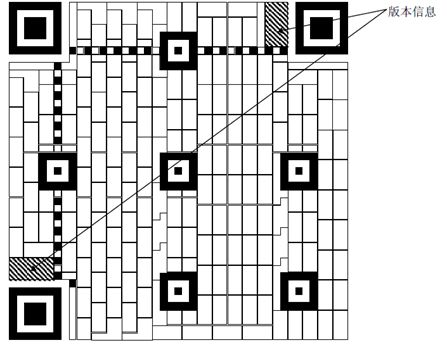
5.4.6 版本信息
版本信息为18 位,其中,6 位数据位即版本号,12个纠错位通过BCH(18,6)编码计算,将数据位和纠错位合起来就是版本信息。
举个例子:
放置在二维码的左下角和右上角,出现两次以提供冗余,与格式信息一样它的正确译码对整个符号的译码也至关重要。
具体每一位放置顺序如下图。
5.4.7 数据和纠错码字
数据和纠错码字的填写也就是我们的上面得到的最终编码的填写,最终编码的填充方式从左下角开始沿着红线填我们的各个bits,1是黑色,0是白色。如果遇到了上面的非数据区,则绕开或跳过。如下图所示。
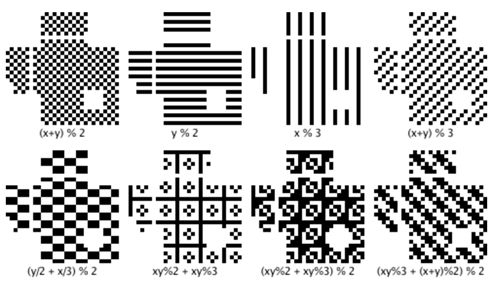
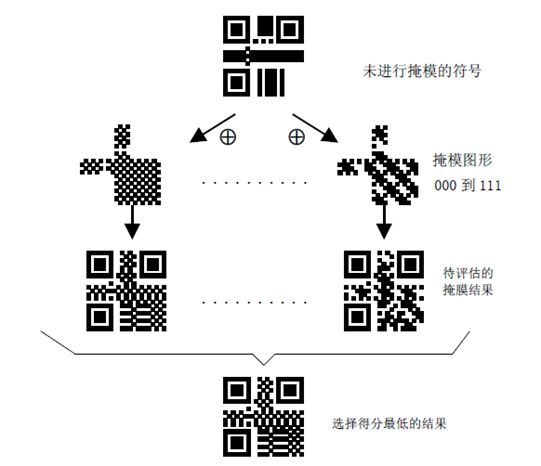
5.4.8 掩码图案
这个阶段时,整个二维码其实已经绘制完成。但是如果只是按照实际的信息来绘制,可能会导致页面上有一大片黑色或者一大片白色,导致扫码时识别困难如下面的左图。所以这一步需要从QR code提供的掩码模板中选一个来和二维码图形做异或操作,生成均匀的黑白交叉的图形如下面的右图。
QR有8个掩码图案你可以使用,如下所示。其中,各个掩码图案的公式生成的结果与原始二维码图做XOR操作。掩码图案只和数据区进行XOR,所以不会影响功能区。
掩码图案并不是都可以符合当前数据,根据特征衡量权值,找到最适合的掩码方式。QR code标准提供的筛选特征:
- 行/列中相临的模块的颜色相同次数
- 颜色相同的模块尺寸
- 在行/纵列中出现深浅深浅深图形
- 整个符号中深色模块的比率
对于原有二维码进行掩码操作过后的二维码就成最终的图了,这个时候我们得到了最终的黑白块均匀的二维码。
5.5 二维码优势
从以上二维码生成过程中不难看出其优点
- 高密度编码,信息容量大。(40个版本,每个版本存储的数据量不同)
- 编码范围广: 该条码可以把图片、声音、文字、签字、指纹等可以数字化的信息进行编码,用条码表示出来;可以表示多种语言文字;可表示图像数据。(分为数字编码、字符编码、字节编码(Byte mode)、日文编码等等,涵盖了日常生活中需要的)
- 容错能力强,具有纠错功能。这使得二维条码因穿孔、污损等引起局部损坏时,照样可以正确得到识读。(四种纠错等级,最高损毁面积达30%仍可恢复信息)。
- 成本低,易制作,持久耐用。
6 个性二维码
这里为什么要介绍个性二维码,正是因为我们通过上面熟悉了其生成流程和原理,才能明白个性二维码的独特性来源于其具有较强的纠错能力!即使二维码部分被覆盖或丢失,依旧能识别出记录的完整信息,其制作思路中心替换法、色彩缤纷法、局部遮挡法、整体造型、出现在不该出现的位置等等,这使得创新设计成为可能。
7 总结
文章首先从二维码怎么从一维码一步步衍生而来,市面上二维码的分类这两部分让我们对二维码有个简单的认识。其次选择了我们生活中最常用的QR code二维码,对于其结构的功能区和数据区做大致介绍。然后对于QR code二维码生成过程中数据码、纠错码、最终编码原理知识进行详细说明,最后从功能区图形的放置、数据区数据的填入、掩码处理对画二维码的流程进行梳理。
也提到了二维码在冗余这个方面的处理,在日常开发中我们讲究去除冗余,但二维码中根据里德-所罗门算法得到的纠错码其实是包含了很多冗余数据的,而这些冗余数据又恰恰是我们能在二维码破坏的情况下能扫出来的原因,也让我们生活中多了形形色色的二维码;画二维码过程中编码格式、信息格式的放置两次也感觉冗余,但是这样才能防止版本、格式重要信息的丢失。所以不同场景下是否需要冗余,以及不同的冗余的方式又起到不一样的作用。
希望通过本篇文章让大家了解到日常生活中的二维码不仅仅是黑白块的组合,而是通过各种明确的规格标准、复杂的编码方式、深奥的数学理论得来,包含了非常值得我们探究的逻辑与知识。
欢迎大家指出有问题的地方,一起进步。
参考:
https://www.cnblogs.com/swordc007/p/9151205.html
https://www.freebuf.com/geek/204516.html
https://www.cnblogs.com/jin20000/p/3424966.html
https://juejin.im/post/58eb05ffb123db1ad06615c9#heading-11
https://coolshell.cn/articles/10590.html