心理声学模型在感知音频编码中的应用

写在前面的话

心理声学模型是我在德国Fraunhofer集成电路研究所（IIS）的国际音频实验室做研究实习的题目，经过半年粗浅的研究，真的觉得非常有趣。实习期间查找并学习了一些文献，真心希望能够和同学们分享、讨论这些知识。在这里想把已公开发表的论文进行翻译整合，并且将自己半年的学习心得整理分享出来。只要有一个同学能从我的一句话中有新的领受，我想就显示出了我写文章的最大意义。希望能够为有需要的同学提供一个关于心理声学模型较为全面的认识，也欢迎指正和讨论分享。

0 引言

感知音频编码（Perceptual audio coding）是利用人类听觉系统的掩蔽特性，通过删除冗余的信息进行存储和传输，从而积极地压缩数字音频。输入的音频信号被分成几帧（frame），并在每一帧内分解为多个频带，称为“子带”（sub band），从而将其划分为时频段（time-frequency segment）。心理声学模型（Psychoacoustic model）分析音频信号并计算掩蔽每个帧和每个子带的量化噪声阈值，因此，它可以在不降低主观音频质量的情况下，最有效地分配比特来表示音频信号。
以滤波器组为核心的心理声学模型是基于巴克尺度(Bark scale)实现的。输入音频信号的掩蔽阈值的第一个近似值是从滤波器组导出的。此外，最终的掩蔽阈值是从听力的绝对阈值与输入音频信号的掩蔽阈值的比较中得出的。根据最终的掩蔽阈值可以计算每个时频段的量化步长，从而实现更恰当的量化。

1 心理声学的基本概念

感知音频编码器是利用人类听觉系统的掩蔽效应，在不降低主观感知音频质量的情况下，删除冗余的信息进行存储和传输。也就是说感知音频编码器是“主动积极地”压缩数字音频，从而使高质量、低比特率的音频信号可以在网络及通信系统中传输。
输入的原音频信号在时间域上被划分为帧，并在每一帧内分解为多个频带，称为“子带”，从而将输入的音频信号其划分为“时频段”。当在每个时频段中对信号进行量化以降低比特率时，会引入量化噪声（quantization noise）。当量化噪声被原音频信号掩盖或低于绝对听力阈值（absolute threshold）时，则无法被听见。因此，如果量化噪声由下沿抵达掩蔽阈值，则可以实现最有效的编码。
心理声学模型（Psychoacoustic model）的功能就是分析原音频信号来计算每个时频段的量化噪声的掩蔽阈值。因此，它可以在音频信号无失真的情况下，最有效地为音频信号的数字表达分配比特。由于提高量化步长会增加量化噪声的强度，所以掩蔽阈值较低的时频段需要被精细地量化。掩蔽阈值较高的时频段则可以被粗糙地量化，以降低比特率。

1.1声音的掩蔽效应 (Auditory masking)

我们都知道一个非常简单的常识，当一个声音较响时，可以部分掩盖另一个声音，使我们听不清楚另一个声音，声音中包含的部分信息会丢失，如果我们继续提高较响声音的音量，那么会导致另一个声音完全被覆盖，无法被听到，这种现象叫做听觉掩蔽，或声音的掩蔽现象。当一种声音的感知受到另一种声音存在的影响时，就会发生听觉掩蔽。
本文中将会主要介绍掩蔽效应与感知音频编码最相关的三个方面：1.时域掩蔽效应；2.频域掩蔽效应；3掩蔽的不对称性。

1.1.1 时域掩蔽效应 (Temporal masking)

时域掩蔽效应是在时域中相邻的声音之间互相的掩蔽效应，或被称为非同时掩蔽。时域掩蔽又分为超前掩蔽（pre-masking或backward masking）和滞后掩蔽（post-masking或forward masking）,下图展示了超前掩蔽和滞后掩蔽的模型，虚线之间是掩蔽声音实际的存在时间。Fastl和Zwicker（2007）提到，由于大脑处理信息需要花费一定的时间，所以感觉（sensation）并不是瞬间存在的，而是需要时间才能被察觉，这就解释了为什么会存在时域掩蔽。掩蔽声音发出之前的一段时间内发生的掩蔽效应，称为超前掩蔽。在已知的研究中，超前掩蔽仅在非常短的时间内有效，即20毫秒（Fastl和Zwicker，2007年）。
当掩蔽声音已经消失时，即当其在物理上不再存在时，仍然会产生掩蔽作用，这种现象就是滞后掩蔽（Fastl和Zwicker，2007年）。 如图1.1所示，滞后掩蔽的强度随时间呈指数衰减，直到100-200 ms后变为零（Fastl和Zwicker，2007； Moore，2012）。由于滞后掩蔽在感知音频编码器的心理声学模型中有重要的影响和作用，所以在3.3节中，我将会介绍具体的模型

1.1.2 频域掩蔽效应 (Frequency masking)

当掩蔽声音和被掩蔽声音同时存在时，就会发生同时掩蔽，即频域掩蔽。例如，一个强纯音会掩蔽在其频率附近同时发声的弱纯音，一个声强为50分贝（dB）、频率为840赫兹（Hz）的纯音，另外还有一个32分贝、850Hz的纯音，在这种情况下只有840Hz的强音能被听见。如果有一个1170Hz的纯音和一个声强比它低18dB的2150Hz的纯音，那么这两个声音会被同时听到。继续提高1170Hz纯音的声强才能够掩蔽2150Hz的纯音，也就是说弱纯音与强纯音的频率越接近，就越容易被掩蔽。带宽越大，则掩蔽效果越强，但存在临界频带(critical band)。由于声音频率与掩蔽曲线不是线性关系，为了从感知上来统一度量声音频率，1961年德国声学家Eberhard Zwicker引入了巴克尺度（Bark scale），这个尺度的范围是从1到24，并且它们与听觉的临界频带相对应。在1.4节中将会详细介绍巴克尺度的转换算法和对应频带。

1.2 掩蔽不对称性 (Asymmetry of masking)

Hellman在1972年指出，掩蔽的不对称性是指噪声对音调的掩蔽比音调对噪声的掩蔽更有效。噪音比复杂的音调具有更强的掩蔽效果。它们之间的不对称度通常达到10到28 dB，最大的不对称度发生在声压级（sound pressure level）为70dB时。在感知音频编码器中使用的心理声学模型应考虑这种效应，通过对声音音调的测量，以获得更准确的掩蔽曲线。
音调和噪音可以通过包络波动的形状来区分，音调的包络波动是缓慢的或规律的，而噪声的包络波动则是强烈的，不规则且更快速的。在3.4节中会介绍音调测量的几种方法：部分光谱平坦度测量（Partial spectral flatness measure）、调幅比（Amplitude modulation ratio）、听觉图像相关性（Auditory image correlation）和时间包络率（Temporal envelope rate）。

1.3 巴克尺度 (Bark scale)

如上所述，在感知音频编码中，输入信号的帧被分解为频谱子带。如下图所示，人耳对声音频率的感知是非线性的，巴克尺度就是从感知上来度量子带的带宽和中心频率。巴克尺度以赫兹为单位，把物理频率映射到心理声学的24个临界频带上。在巴克尺度上相等的距离对应于在感知上相等的距离，也就是说1个感知临界频带的宽度等于一个巴克。下表展示了巴克尺度的中心频率、临界带宽以及边界频率之间的关系。

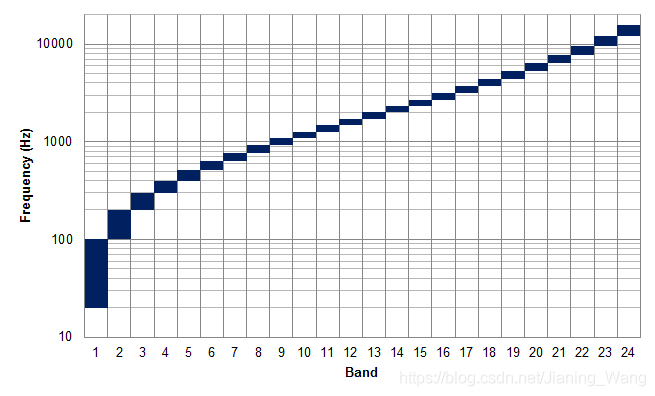
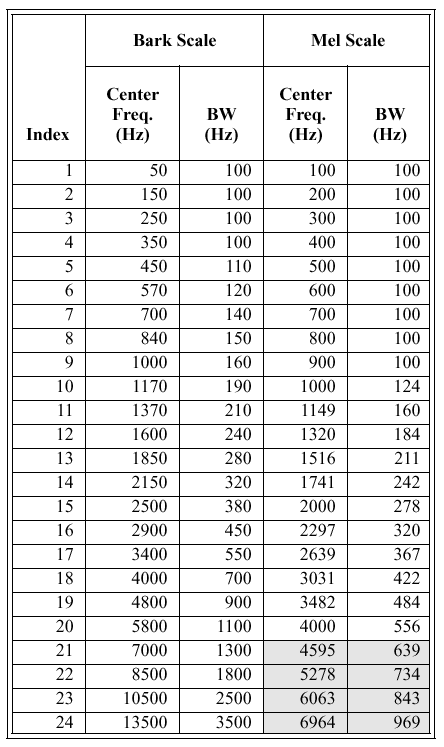Zwicker（1956，1961）及其团队（1957）在各种情况下通过实验测量了听觉滤波器的带宽。在1980年Zwicker和Terhardt为临界带宽（CB）提出了以下公式：
$$CB=25+75[1+1.4(0.001f{)}^2{]}^{0.69}$$
$f$是中心频率，且与临界带宽（CB）的单位同是赫兹（Hz）。在2007年，Fastl和Zwicker提出了一种更简单的求临界带宽近似值和巴克数（Bark number）的方法：
$$CB=\{\begin{array}{ll}100& \text{if f < 500}\\ 0.2f& \text{else}\end{array}$$
$$Barknumber=13\arctan (0.00076f)+3.5\arctan ((\frac{f}{7500}{)}^2)$$

2 感知音频编码 (Perceptual audio coding)

我们可以使用随时间连续变化的电压来模拟声波。但是在现代系统中更常使用数字信号表示，可以使用模数转换器来转换连续电压信号，以规律的时间间隔测量或采样连续模拟波形的幅度，并将样本存储为一系列代表幅度的数字（Oppenheim，Schafer，2010； Proakis，Manolakis，2007）。采样率应足够高，以确保波形可以从样本中完美重构。否则将会发生混叠。
量化是指将输入信号的连续取值近似为有限多个（或较少的）离散值的过程。输入信号与其量化信号之间的差值被定义为量化误差，是由诸如舍入和舍位之类的量化过程引起的。在还原信号的数模转换后，量化误差会被再生为量化噪声。提高量化精度能够把噪声降低到无法察觉的程度，听觉系统的局限性可以用来确定量化的精度，因为人类听觉系统听不到幅度微小的变化。
感知音频编码器就是利用人类听觉系统的局限性来正确选择量化精度，从而以最有效的方式重建与原始信号具有相同主观感知质量的信号。数字信号可以表示为二进制数字或比特的序列。例如，常用的“高保真”数字信号的比特率是768000 比特/秒（bit/s）。

2.1 感知音频编码器的基本结构

感知音频编码主要用于通过去除多余的信息进行存储和传输来降低比特率并保持高音频质量，这被称为“积极压缩”。
编码器的输入信号通常是脉冲编码调制（Pulse Code Modulation）信号，为了跟踪音频信号的时间变化，通常将音频输入信号分为多个时频段。首先将信号在时域分成帧并分别进行处理。然后将每一帧进行频谱分解，将每个帧中的内容划分为多个子频带，以进行频率分析，可用到的工具例如改进的离散余弦变换（MDCT）或滤波器组。
尽管量化过程会引起量化噪声，通过量化每个帧和每个频带中的信号可以降低数字表示的数据速率。如果量化噪声被输入音频信号掩蔽或低于绝对听觉阈值，则无法被听见。因此，如果量化噪声刚好低于其掩蔽阈值，则可获得最有效的编码。该曲线可以称为“输入信号的掩蔽曲线”或“量化噪声的掩蔽阈值”。

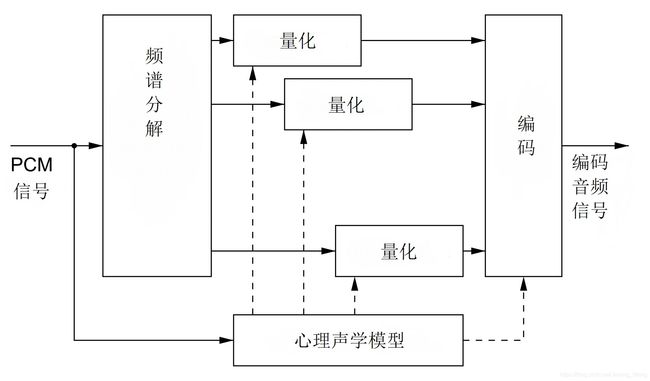
因此，通过使用心理声学模型来估计掩蔽阈值，可以控制每一帧的每个子带的量化精度，即量化步长。如上所述，在应用了心理声学模型的压缩过程之后，普通听众不会察觉到量化噪声。

2.2 改进离散余弦变换 (The modified discrete cosine transform)

改进离散余弦变换(The modified discrete cosine transform (MDCT))是一种基于时域混叠抵消（TDAC）技术的时频分解工具。在保证编码性能的情况下有效地避免了加窗离散余弦变换(DCT)块处理运算中的边缘效应，从而有效地去除由边缘效应产生的周期化噪声。凭借这种优势，被广泛应用于语音和图像信号的变换编码中。

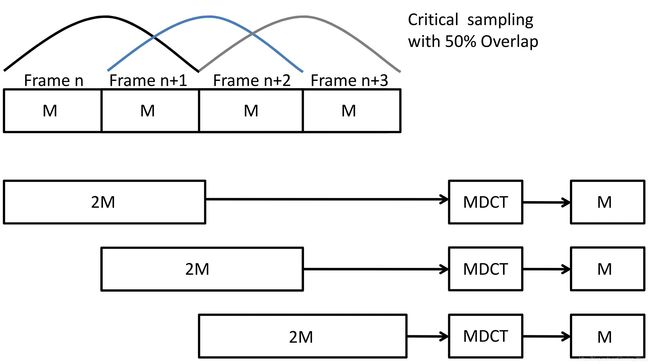
它被设计为在较大数据集的连续块上执行，一个块的后半部分与下一个块的前半部分重合。 上图是Taghipour受到Painter和Spanias的理论启发提出的MDCT的分析转换图。可以看出，MDCT在两个相邻帧之间使用了$50％$的重叠。
如图中所示，MDCT分析需要$2M$个输入样本才能生成$M$个频谱系数。$n$表示时间样本的序号，$k$表示频谱系数的序号，给定输入序列$x(n)$ ，经过改进离散余弦变换后会生成$M$个频域序列系数$X(k)$ ，如下所示（Painter and Spanias, 2000）：
$$X(k)=\sum _{n=0}^{2M-1}x(n)h_k(n),0\le k\le M-1$$
可以看到，这种变换是由$M$个分析基础函数$h_k(n)$和输入序列$x(n)$的内积来实现的。其中余弦调制函数的形式为：
$$h_k(n)=w(n)\sqrt[]{\frac{2}{M}}\cos \left(\frac{(2n+M+1)(2k+1)\pi }{4M}\right)$$
$w(n)$是窗长为$2M$的窗函数。在被设定为奇数堆叠的MDCT中经常使用的窗口函数是Edler在1989年提出的正弦窗函数，其中$0\le n\le 2M$：
$$w(n)=\sin \left(\frac{(n+0.5)\pi }{2M}\right)$$
原始数据的完美重构性是可以通过MDCT的合成变换，即所谓的“逆变换”（inverse MDCT(IMDCT），来实现的（Painter和Spanias，2000），其中$0\le n\le M-1$：
$$x(n)=\sum _{k=0}^{M-1}[X(k)h_k(n)+X^P(k)h_k(n+M)],0\le n\le M-1$$
$X^P(k)$表示变换系数的前一个块。 下图显示了IMDCT在其输出端提供了$2M$个样本以及重叠加法合成，从而产生了$M$个输出样本的帧（组块）。 一般来说合成变换所用的窗口与MDCT变换中所用的窗口相同。

2.3 量化和量化噪声 (Quantization)

量化是将输入值从一个较大的集合（通常是一个连续的集合）映射到一个较小的集合（通常包含有限数量的元素）中的输出值的过程。模数转换器是一种典型的量化器。
量化基本上是所有有损压缩算法的核心。通过减少冗余信息，感知音频编码器可以实现更低的数据速率和更高的效率。通过选择量化步长，可以调整量化精度和压缩程度。

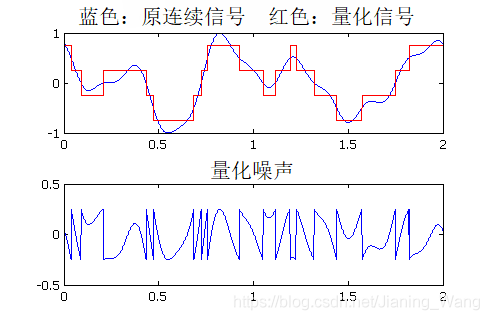
上图显示了量化过程，例如舍入和截断，会在音频信号中引入“量化误差”，这种误差会在信号重建后再生为量化噪声。为了获得高保真的信号，通过使用高精度量化可以降低量化噪声。高精度的量化也意味着更高的比特率。
因此，需要在高质量音频传输和低比特率之间进行权衡。换句话说，如果量化噪声刚好低于其掩蔽阈值，则可以达到最有效的比特分配，该比特分配也意味着可以得到没有可听见的量化噪声的音频信号。这条掩蔽曲线如何在心理声学模型中生成将在第三章心理声学模型中描述。

3 心理声学模型(Psychoacoustic model)

如第一章中所述，心理声学模型分析音频信号并计算每个帧和子带的量化噪声的掩蔽阈值，从而可以消除音频信号中的可被感知到的量化噪声。
Taghipour等人（2010，2014b）提出了下图的基于过滤器组的心理声学模型。在模型中的第一步就是通过滤波器组将音频信号分解成其频谱分量（Taghipour等人，2010，2013b，2014b; Chen等人，2014）。滤波器组是根据人耳听觉系统的特性被设计的，这一点将会在3.1和3.2节中详细介绍。模型中下一个组件是对滞后掩蔽进行建模。随后将会基于时频段的音调程度，对估计的掩蔽阈值进行缩放。并根据各个信道输出的加权组合来建立掩蔽阈值，并将其映射到MDCT的频域上。 在模型的最后一步，通过在输入音频的掩蔽阈值与绝对听力阈值中取较大值，可以输出最终的掩蔽阈值。 在下文中，将更详细地描述心理声学模型中每个组件的理论背景和功能。

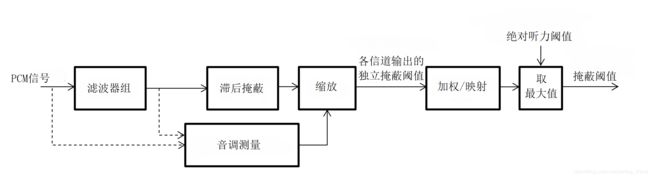
3.1 外周听觉系统 (The peripheral auditory system)

本节将简要介绍外周听觉系统(The peripheral auditory system)的生理学和心理生理学的相关基本知识。人类外周听觉系统可以被视为将被发送到听觉神经的信号的预处理系统。心理声学模型就是根据人类听觉系统的外周结构和某些心理声学现象进行建模。
如图（Fastl和Zwicker，2007年）所示，外围听觉系统可分为三个部分：外耳，中耳和内耳。

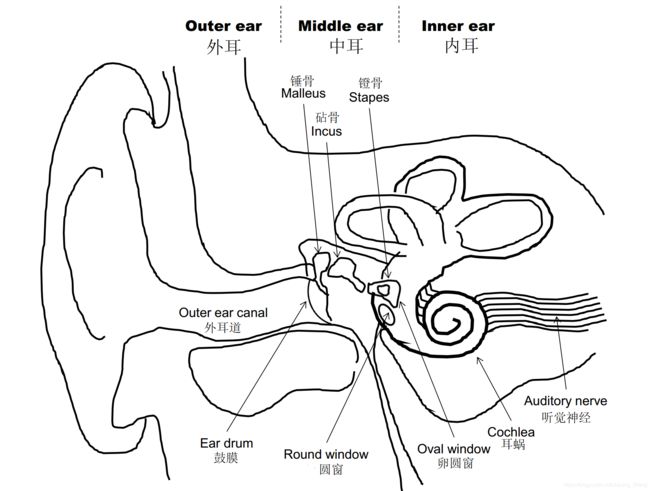
外耳是人类听觉系统的最外部分，由耳廓和耳道组成。外耳的功能是收集声能，并通过耳道将其传输到鼓膜（Fastl和Zwicker，2007年）。外耳道可以保护耳膜，并使内耳非常靠近大脑，从而使动作电位的传播时间缩短（Fastl和Zwicker，2007年）。耳廓起着声波反射器和衰减器的作用，同时可以帮助大脑识别声音起源的方向。
如图所示，从鼓膜到卵圆窗的区域称为中耳，由三块小骨（锤骨、砧骨和镫骨）组成了听骨链。杠杆状的听骨链会将声波击中鼓膜时产生的声音震动转换为更高压力的震动，这些转换后的振动（仍为波形）会进入充满空气的卵圆窗。
内耳的结构十分复杂，本文中只讨论与感知编码最相关的部分，即耳蜗。耳蜗是一螺旋形骨管，绕蜗轴卷曲两周半，形似蜗牛壳。如下图展开的耳蜗示图，其中波从基部（在中耳和卵圆窗附近）传播到顶点（螺旋体的顶部）。

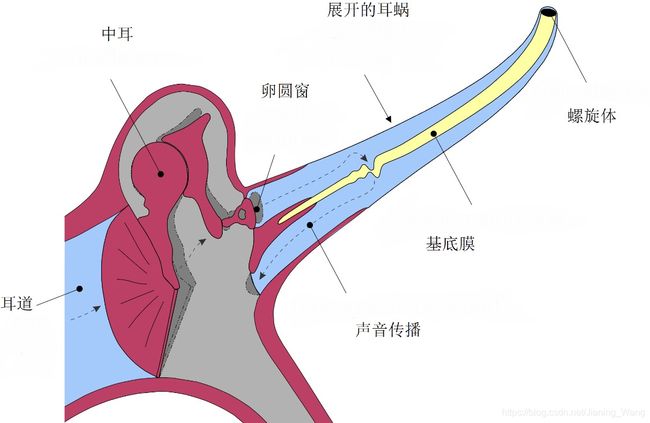
耳蜗充满了内淋巴，一种水状液体，可响应来自中耳的振动而移动。因此，在基底膜上施加了压力差，使基底膜移动，基底膜上排列有毛细胞，是声音感受细胞。基底膜的运动导致纤毛运动，这种运动被转换为神经冲动，沿着听觉神经传递到大脑以进行进一步处理。基底膜和纤毛的运动机理如下图所示。

根据现有研究，由于基底膜的厚度和宽度从基部到顶部是变化的，所以基底膜的不同区域会响应不同的正弦频率振动。高频信号分量无法使大量流体移动，所以基端附近的狭窄但僵硬的基底膜会响应高频震动。低频分量可以使大量流体运动，并且由于它们振荡缓慢，可以首先在顶点附近刚度较小的基底膜部分引起震动。
这种特性被称为“Tonotopy”（Fletcher，1940），表示内耳中不同频率声音的空间排列。Tonotopy是生理学名词，tono来自希腊语“频率”，topos表示“位置”。下图展示了不同频率声音在基底膜上的不同空间分布。

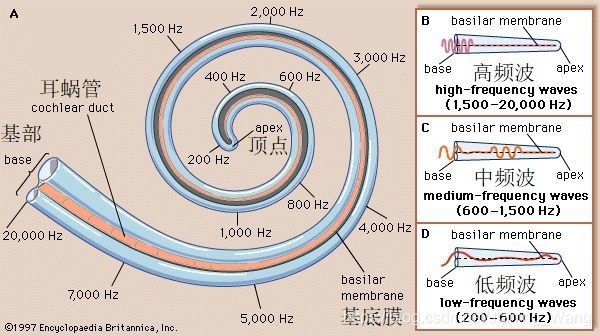
可以根据这一性质对心理声学模型的滤波器组进行设计，以分析耳蜗对输入音频信号的处理。因此，感知音频编码器不仅需要在时域对输入音频信号进行分析，而且也必须基于其频谱分量进行分析。

3.2 滤波器组 (The filter bank)

伽马通滤波器（Gammatone filer）是听觉系统中广泛使用的听觉滤波器模型，是一种由脉冲响应描述的线性滤波器。其时域脉冲响应为：
$$g(t)=a{t}^{n-1}{e}^{-2\pi bt}\cos (2\pi f_{c}t+\phi )$$
$a$为滤波器增益，$t$是时间（单位是秒），$n$是滤波器的阶数（通常取4），$b$为滤波器的衰减因子并与滤波器的带宽有关，$f_c$是中心频率，$\phi$是载波的相位。
该滤波器的设计是基于巴克尺度的，从该滤波器组中输出的就是输入音频信号的掩蔽阈值的第一个近似值。

3.3 滞后掩蔽效应 (Forward masking)

在2007年，Fastl和Zwicker指出当掩蔽声音已经消失时，仍然会对后续帧产生掩蔽作用，这种现象就是滞后掩蔽。现有的研究表明，滞后掩蔽的强度随时间呈指数衰减，直到100-200 ms后变为零（Fastl和Zwicker，2007； Moore，2012）。
在Taghipour提出的心理声学模型中，使用电阻电容电路来建模实现衰减指数函数，如图所示。

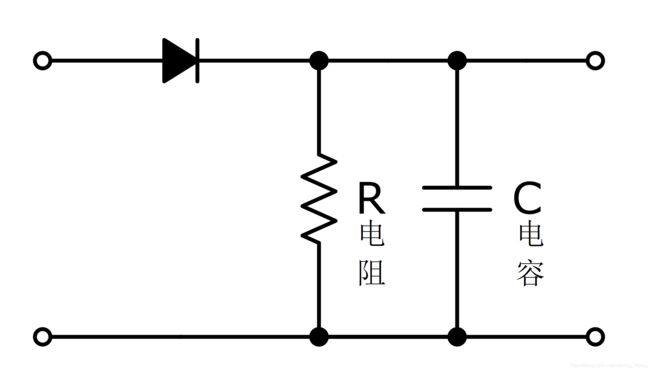
3.4 音调测量和缩放 (Level scaling based on tonality measure)

输入音频信号或滤波器的输出被用作音调测量模块的输入。用来估计音频信号属于音调或噪声的方法通常称为“调性估计方法（tonality estimation methods）”（Painter和Spanias，2000； Pulkki和Karjalainen，2015）。类似音调的音频段包络波动是非常缓慢的，甚至没有波动。相反，类似噪声的时频段具有强烈的，不规则的和较快速的包络波动。心理声学模型应根据时频段的音调或噪声特征来调整掩蔽曲线的水平。
比较常见的几种调性估计方法有：部分光谱平坦度测量（PSFM）、调幅比（AM-R）、听觉图像相关性（AIC）和时间包络率（TE-R）。

3.5 映射 (Mapping)

从滤波器输出许多频率子带的掩蔽阈值。 由于量化是在MDCT域中执行的，因此在每个MDCT频率上，由心理声学模型计算出的掩蔽阈值应通过线性插值映射到MDCT的光谱分辨率上，应将屏蔽阈值映射到MDCT的频谱分辨率上。频率轴转换可以由稀疏矩阵实现。

3.6 绝对听力阈值 (Absolute threshold)

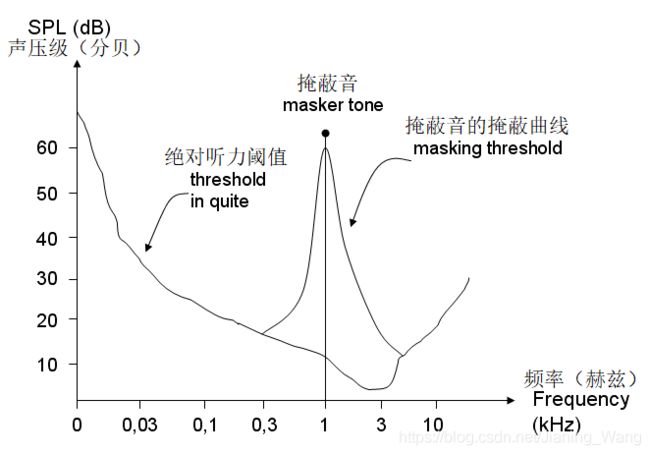
在第1章中已经介绍了掩蔽效应，本节将会引入绝对阈值及其在心理声学模型中的应用。绝对听觉阈值是指正常听觉的普通听众在没有其他声音的情况下可以听到的纯音的最小声级，即安静时的阈值。听力阈值与频率相关，如图所示，在1kHz至5kHz之间的频率下人耳是最敏感的。生成掩蔽曲线的最后一步是将每个时频段中经过缩放和映射的的掩蔽阈值与相应频率的绝对阈值进行比较。当输入音频信号频率分量的幅度低于绝对阈值的幅度时，频率分量的幅度将被这些频率点处的绝对阈值的幅度覆盖。 换句话说，在此步骤中，心理声学模型将在每个时频段处从两条曲线中保留更高的幅度，这可以使编码更有效。

参考文献

[1] F. Baumgarte, C. Ferekidis, and H. Fuchs, A nonlinear psychoacoustic model applied to iso/mpeg layer 3 coder, in Audio Engineering Society Convention 99, Audio Engineering Society, 1995.

[2] V. Britanak and K. R. Rao, Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations, Springer, 2017.

[3] S. Chen, R. Hu, and N. Xiong, A multimedia application: spatial perceptual entropy of multichannel audio signals, EURASIP Journal on Wireless Communications and Networking, 2010 (2010), pp. 1-13.

[4] J. D. Durrant, N. R. Dunnick, J. H. Lovrinic, R. W. McCallum, and C. M. Sandler, Bases of hearing science, Williams & Wilkins, 1977.

[5] B. Edler, Coding of audio signals with overlapping block transform and adaptive window functions, Frequenz, 43 (1989), pp. 252-256.

[6] H. Fastl and E. Zwicker, Information processing in the auditory system, in Psychoacoustics, Springer, 2007, pp. 23-60.

[7] H. Fletcher, Auditory patterns, Reviews of modern physics, 12 (1940), p. 47.

[8] S. A. Gelfand, Hearing: An introduction to psychological and physiological acoustics, CRC Press, 2016.

[9] K. Krishnamurthy and T. Deif, Audio compression using entropy coding and perceptual noise substitution, MUSIC 422, Stanford University, (2009).

[10] S. Mittal and J. S. Vetter, A survey of architectural approaches for data compression in cache and main memory systems, IEEE Transactions on Parallel and Distributed Systems, 27 (2015), pp. 1524-1536.

[11] B. C. Moore, An introduction to the psychology of hearing, Brill, 2012.

[12] A. V. Oppenheim and R. W. Schafer, Discrete-time signal processing 3rd edn (harlow, 2010.

[13] T. Painter and A. Spanias, Perceptual coding of digital audio, Proceedings of the IEEE, 88 (2000), pp. 451-515.

[14] A. Spanias, T. Painter, and V. Atti, Audio signal processing and coding, John Wiley & Sons, 2006.

[15] A. Taghipour, Psychoacoustics of detection of tonality and asymmetry of masking: implementation of tonality estimation methods in a psychoacoustic model for perceptual audio coding, (2016).

[16] S. van de Par, A. Kohlrausch, R. Heusdens, J. Jensen, and S. H. Jensen, A perceptual model for sinusoidal audio coding based on spectral integration, EURASIP Journal on Advances in Signal Processing, 2005 (2005), p. 317529.

[17] B. Widrow and I. Kollar, Quantization noise in digital computation, signal processing control and communications, 2008.

[18] E. Zwicker and H. Fastl, Psychoacoustics: Facts and models, vol. 22, Springer Science & Business Media, 2013.