04.卷积神经网络 W1.卷积神经网络

参考：
吴恩达视频课
深度学习笔记

1. 计算机视觉

举例：图片猫识别，目标检测（无人驾驶），图像风格转换（比如转成素描）等等

面临的挑战：

• 数据的输入可能会非常大
• 一张1000×1000的图片，特征向量的维度达到了1000×1000×3(RGB,3通道) = 300万
• 在第一隐藏层中，你也许会有1000个隐藏单元，使用标准的全连接网络，这个矩阵的大小将会是1000×300万，矩阵会有30亿个参数
• 在参数如此大量的情况下，难以获得足够的数据来防止神经网络发生过拟合，处理30亿参数的神经网络，巨大的内存需求也受不了

你希望模型也能处理大图。为此，你需要进行卷积计算，下节将用边缘检测的例子来说明卷积的含义

2. 边缘检测示例

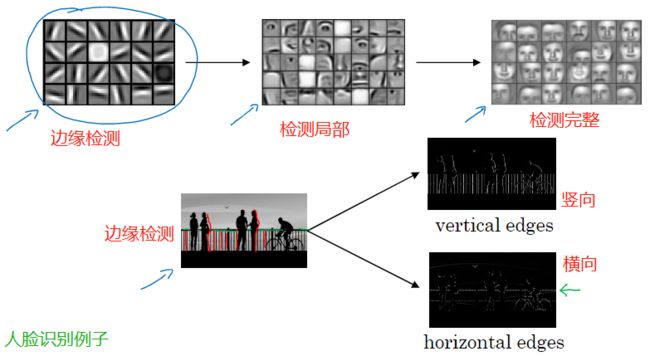
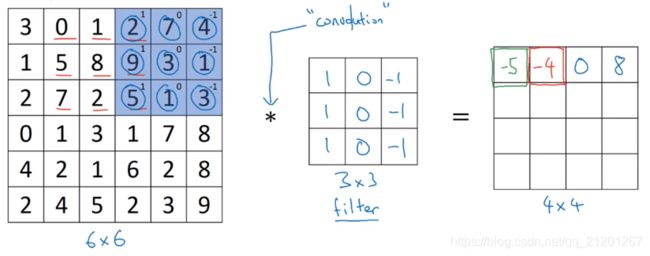
例如 6x6 的单通道灰度图像，检测垂直边缘，构造一个矩阵$\left[\begin{array}{rrr}1& 0& -1\\ 1& 0& -1\\ 1& 0& -1\end{array}\right]$ （过滤器 / 核），进行卷积运算*（convolve）

import numpy as np
image = np.array([[3,0,1,2,7,4],[1,5,8,9,3,1],[2,7,2,5,1,3],[0,1,3,1,7,8],[4,2,1,6,2,8],[2,4,5,2,3,9]])
print(image)
print('-------')
filter_ = np.array([[1,0,-1],[1,0,-1],[1,0,-1]])
print(filter_)
print('-------')
from scipy import signal
convolution = -signal.convolve2d(image, filter_, boundary='fill',mode='valid')
print(convolution)

[[3 0 1 2 7 4]
 [1 5 8 9 3 1]
 [2 7 2 5 1 3]
 [0 1 3 1 7 8]
 [4 2 1 6 2 8]
 [2 4 5 2 3 9]]
-------
[[ 1  0 -1]
 [ 1  0 -1]
 [ 1  0 -1]]
-------
[[ -5  -4   0   8]
 [-10  -2   2   3]
 [  0  -2  -4  -7]
 [ -3  -2  -3 -16]]

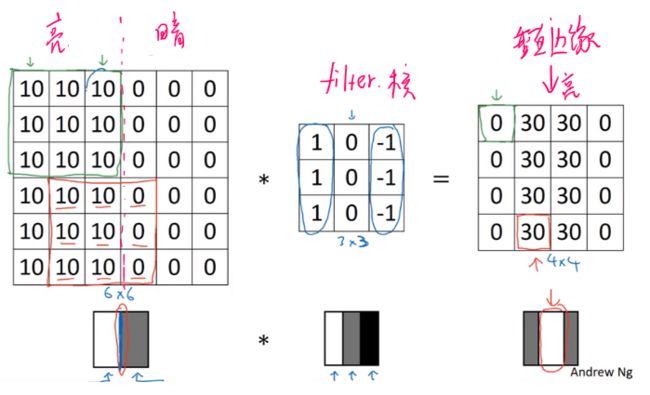
为什么可以检测边缘？

image = np.array([[10,10,10,0,0,0],[10,10,10,0,0,0],[10,10,10,0,0,0],[10,10,10,0,0,0],[10,10,10,0,0,0],[10,10,10,0,0,0]])
filter_ = np.array([[1,0,-1],[1,0,-1],[1,0,-1]])
print(-signal.convolve2d(image, filter_, boundary='fill',mode='valid'))

[[ 0 30 30  0]
 [ 0 30 30  0]
 [ 0 30 30  0]
 [ 0 30 30  0]]

3. 更多边缘检测

可以检测明暗变化方向

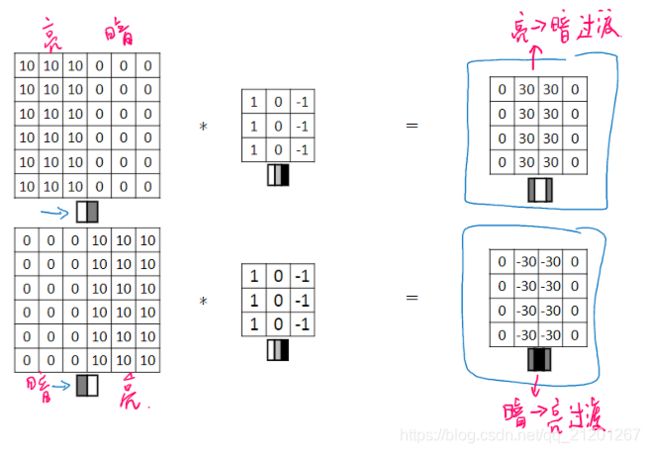
竖直，水平的过滤器


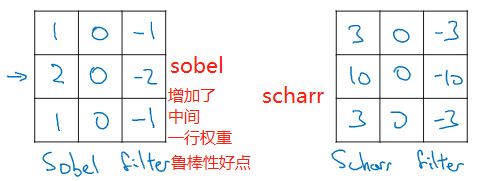
把这9个数字当成参数，通过反向传播学习，边缘捕捉能力会大大增强（可以检查任意角度）

4. Padding

上面 6x6 的图片，经过一次过滤以后就变成 4x4 的，如果经过多层，最后的图像会变得很小。

假设原始图片是 $n\times n$，过滤器是 $f\times f$，那么输出大小是 $(n-f+1)\times (n-f+1)$

• 缺点1，图像每做一次卷积，缩小一点，最后变得很小
• 缺点2，在角落或边缘区域的像素点在输出中采用较少，丢失了图像边缘位置的许多信息

解决上面的问题：

• 进行卷积操作前，沿图像边缘填充 p 层像素，令 $(n+2\ast p)-f+1=n\Rightarrow p=\frac{f-1}{2}$， 这样可以保持图像大小不变
• 还使得边缘信息发挥作用较小的缺点被削弱

$p$ 填充多少层，怎么选？

• Valid 卷积：$p=0$
• 和 Same 卷积：$p=\frac{f-1}{2}$，$f$ 通常是奇数（对称填充，有中心点）

5. 卷积步长

每次过滤器在图片中移动 s 步长（上面的 s = 1）

输出尺寸为 $(\frac{n+2p-f}{s}+1)\times (\frac{n+2p-f}{s}+1)$，向下取整

数学中的卷积，需要在操作之前对过滤器顺时针旋转90度 + 水平翻转，深度学习里省略了该步骤，但是不影响，简化了代码

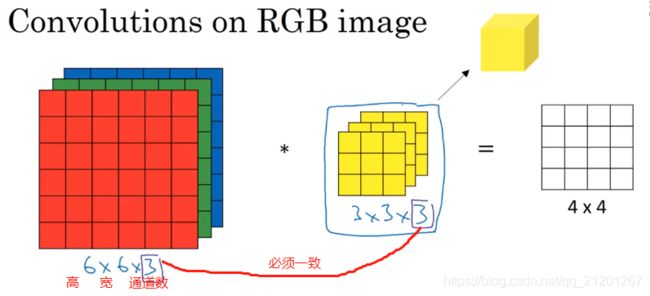
6. 三维卷积

输出是一个二维的，每个格子里是对应着 27个元素求和

如果希望对不同的通道进行检测边缘，对 filter 的相应层设置不同的参数就可以了

想要多个过滤器怎么办？（竖直的、水平的，各种角度的）

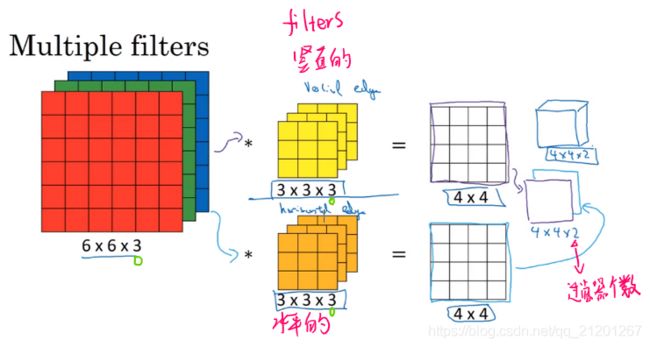
7. 单层卷积网络

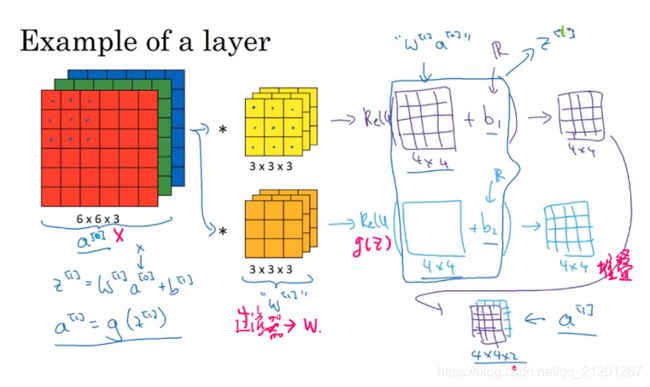
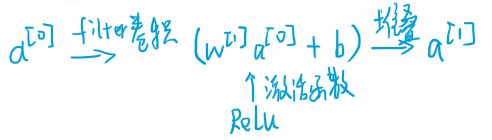
参数的个数跟图片大小无关，跟过滤器相关，假如有10个过滤器，上面每个过滤器有 27 个参数，加上 偏置 b，28个再乘以10，共计280个参数

即使图片很大，参数却很少，这就是卷积神经网络的一个特征，叫作“避免过拟合”。

8. 简单卷积网络示例

除了 卷积层（convolution），还有 池化层（pooling），全连接层（fully connected）

9. 池化层

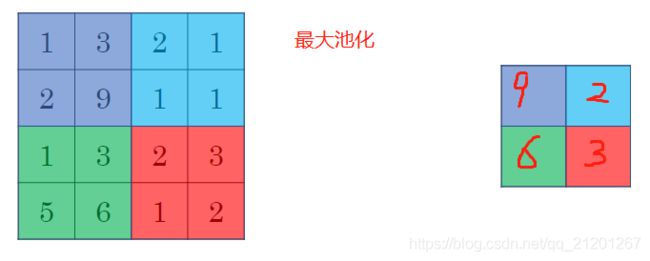
除了卷积层，卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性

Max 运算的实际作用：

• 如果在过滤器中提取到某个特征，那么保留其最大值
• 如果没有提取到这个特征，可能在右上象限中不存在这个特征，那么其中的最大值也还是很小

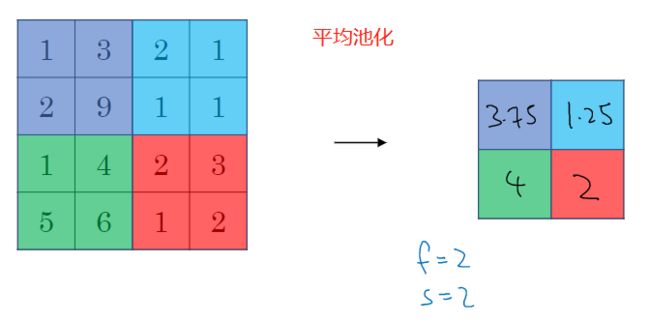
池化，它有一组超参数 $f,s$，但没有参数需要学习，不需要梯度下降更新

最大池化比平均池化更常用

常用的参数值为 $f=2\text{ or }3,s=2$
最大池化时，很少用到 padding（$p=0$）
输入输出通道数一样
最大池化只是计算神经网络某一层的静态属性，没有需要学习的参数

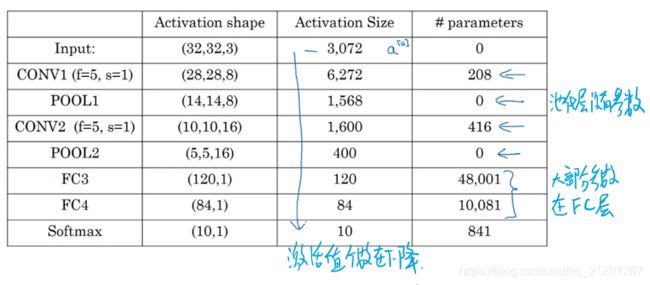
10. 卷积神经网络示例

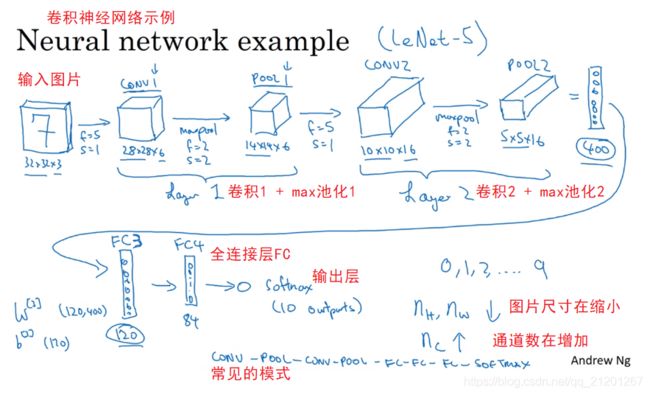
尽量不要自己设置超参数，而是查看文献中别人采用了哪些超参数，选一个在别人任务中效果很好的架构，它也有可能适用于你的应用程序

11. 为什么使用卷积？

和只用全连接层相比，卷积层 的两个主要优势在于参数共享和稀疏连接

• 全连接层的参数巨大，卷积层需要的参数较少

原因：

1. 参数共享，特征检测如果适用于图片的某个区域，那么它也可能适用于图片的其他区域
2. 使用稀疏连接，一个输出仅依赖少部分的输入
   
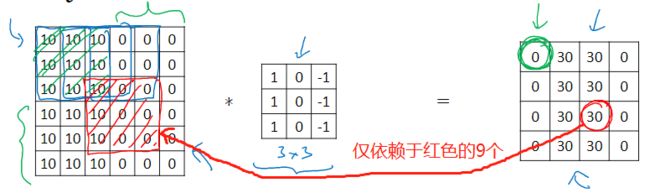
   神经网络可以通过这两种机制减少参数，以便我们用更小的训练集来训练它，从而预防过度拟合

作业

待写，见下一篇

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！