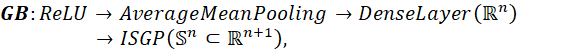Sphere GAN的（粗糙的）个人翻译

 

## Sphere GAN的（粗糙的）个人翻译

前言：其实这本来是老师布置的假期作业，既然翻译完了，就发了上来
由于个人水平有限，其中出现了什么错误望不吝赐教

> 原文见：http://cau.ac.kr/~jskwon/paper/SphereGAN_CVPR2019.pdf

Sphere Generative Adversarial Network Based on Geometric Moment Matching

关键名词的解释：

1. IEEE: Institute of electrical and electronics engineers 中译为电子与电气工程师学会
2. CVPR: Conference on computer vision and pattern recognition 中译为（IEEE）国际计算机视觉与模式识别会议
3. Gradient penalty term: 中译为梯度惩罚项，是一种机器学习中的数学算法
4. Wesserstein距离: 又叫做Earth-Mover距离，这是用于衡量两个分布间的距离，公式为：

1. Hypersphere: 中译为超球/多维球体，即一个展现出三个以上维度的球体，也叫做黎曼流形
2. IPM：积分概率测量理论
3. GAN对抗性神经网络
4. virtual data sampling techniques:虚拟采样技术，我只知道这是游戏里面拿来抗锯齿的
5. Kullback-Leibler （KL）：相对熵
6. Adam optimizer：Adam优化器，在tensorflow的一种优化程序

我目前不明白的部分

1. soft consistent:如果说self-consistent意思是自洽性，就是无自我矛盾，那soft consistent是不是软件的一致性？？？抑或是有序性？

2、we show that sphere GAN

is closely related to IPMs and that minimizing the pro-

posed distance amounts to minimizing the multiple

Wesserstein distances of probability measures on the

n-dimensional hypersphere.这句话我没有看明白……

3、loses the diversity of representations ：这应该翻译为缺少细节吧？

4、pdf第六页（FID overcomes the problems of IS by estimating the 2-Wasserstein distance of Gaussian distributions induced by the outputs of hidden activation）

 

（水印部分）

此CVPR的论文由计算机视觉基金会提供对外参阅，除去此水印中的内容，该论文的所有内容与真实存在的版本完全一致，本文的最终解释权归属于IEEE Xplore机构

（水印部分）

基于几何矩阵匹配的球形生成对抗网络

作者：……

概述

我们基于积分概率测量理论提出了生成球形的对抗性神经网络理论，辅以IPM边缘计算技术来使计算机获得识别球体的功能从而达到训练程序的目的。在多维球体中，球形GAN利用从几何矩阵匹配通过高阶统计学加工得出来的数据以得到更为精确的结果。

在本论文中，我们将从数学的角度阐明GAN球体的性质。
在本论文的实验中，无论是从数量上评价，还是以质量为度量，GAN球体从CIFAR-10、STL-10和LSVN室体资料集中生成的结果，都证明了该理论的优越性与先进性。

源代码详见：……

介绍

自从Goodfellow等人发明了几何矩阵匹配技术，该技术便吸引了越来越多的研究人员投入其中，这些研究人员利用GAN技术在诸如图像生成、图像编辑、视觉追踪、3D重建/分割、物体检测、强化学习、医学影像等计算机视觉识别领域做出了重大的贡献，有着广泛而深远的影响。

通常GAN技术会尝试以最少的散度来辨明数据的真假。因此，它的引擎会期望它所产生的数据足够简单让数据看起来是真实可信的，并且鉴别器会尝试识别出真实的数据。尽管GAN技术已经在各种任务上成功应用，但训练GAN程序是一个困难等过程，也就是说它难堪大任。例如，频繁的动态训练可能会导致GAN程序的不稳定，并且在某些模块上会有崩溃的风险。

当越来越多的类GAN技术以及他们的应用得以提出，在本文我们将着重于讨论基于IPMS的类GAN技术如何克服上述问题。

基于IPM的GAN技术在物体识别功能中利用梯度惩罚项或软件自洽项以达到稳定学习的目的，能效得以显著提高。然而这些额外的项目不免带来一些需要改定的超参数，产生了更多的算力开销。此外，由于样本数据的约束，许多基于IPM的GAN技术会变得不稳定，并且WGAN技术仅仅利用了一阶统计与双重1——Wesserstein距离。

我们在本文中提出了一个球形GAN引擎，球形GAN利用对抗性网络与对样本数据经过高阶统计加工所得信息来取得更为精确的结果。由于对抗网络基于多维球体理论运行，IPM理论在球形GAN中得以有界。

我们将会展示多维球体理论中的几何约束条件如何令GAN更为稳定地运行。球形GAN采用了拥有数学理论支持的黎曼流形（即高维球面）而不依赖于虚拟采样技术与额外的梯度惩罚项目。

本文主要申明的观点如下：

1. 我们认为球形GAN这种新理论比传统的基于IPM的GAN旧理论更具优势。据我所知，球形GAN是第一个利用黎曼流形在GAN物体识别功能中定义IPM的理论。此外，它还是第一个淘汰了虚拟采样技术以及梯度惩罚项的新型技术。
2. 球形GAN理论的优越性已经得到证明。在第四章节中

？？？

3、在无人工干预的CIFAR-10，STL-10和LSUN室体数据集图像生成问题，由于球形GAN技术能够有效的匹配特征空间中短发高阶距，球形GAN的精读得以大幅提高，球形GAN的性能高于类基于IPM高GAN技术。

2.相关工作

当我们利用基于相对熵（KL）分歧的差异测量法时难以在细微的差别中区分出两个无重叠概率分布的距离。为了解决这一难题，（有的研究人员）以基于IPM理论的GAN引擎的变种为基础进行二次创新，提出了新颖的基于KL分歧理论的GAN引擎。在IPM理论中，两个概率分布之间的距离由通过对某类功能的期望的最大差异来衡量，这使得在基于IPM的GAN引擎中选择合适的功能类别至关重要。在本章节中，我们将讨论几个基于IPM理论的GAN引擎的变种的优劣。

Wesserstein 距离：WGAN以及它的变种使用Wesserstein公制来辨明图片的真假。在此类方法中，鉴别器作为利普希茨（Lipschitz ）实值1函数的一个模块，负责输出一个欧氏空间。WGAN多次修改鉴别器的权重，使它们处于紧凑的区间[-c，c]中来实施利普希茨条件。然而，反复修改权重会造成程序学习不稳定并且出现负优化（sub-optimal ）的结果。为了克服这一缺陷，研究人员提出了带有梯度惩罚的WGAN（即WGAN-GP）。但是，因为这个方法每次需要计算梯度惩罚项的技术，所以这个方法在每次机器学习中都需要消耗两倍的时间。WGAN-CT通过使梯度惩罚项与有悖于1-利普希茨条件的软件一致性相结合来克服了这个问题。WGAN-GP与WGAN-CT皆展现了它们优异的性能，单无论哪种方法都需要额外的惩罚项，这就可能导致软件错误地选择惩罚权重时负优化的产生。

WGAN-CT训练具有优良启发式的网络，相比之下，球形GAN无需对虚拟数据点进行采样。与WGAN-GP、WGAN-CT和WGAN-LP不同，球形GAN无需额外的梯度惩罚项，这使得训练时间更加短暂。我们通过实践证明了球形GAN无需梯度约束仍然正常输出结果。

最大平均值差异（MMD）距离：WGAN在鉴别器网络中仅仅匹配一阶距。相比之下，MMD GAN匹配希尔伯特（Hilbert）空间中单位球上所定义的无限阶距。MMD GAN额外花费一些时间用于高阶统计，然而，它使用自动编码器来向学习网路传入数据，并且通过权重裁剪来限制梯度以达到稳定学习的目的。所以，（the objective functions应该指的是“使用自动编码器来向学习网路传入数据，并且通过权重裁剪来限制梯度以达到稳定学习的目的”这个功能）那个功能会导致网络的可用容量降低。由于像素空间是高纬度的（也就是说：因为照片拍出来是二维的，而我们需要计算的是三维空间），所以MMD距离无法很好地处理复杂的自然图片。这是因为这样，MMD距离会产生低劣的样本并且（缺少细节？）。

其他IPM：众所周知，具有特定内核的平方MMD等于能量距离。Crame ́r GAN 使用能量距离来训练GAN。通过神经网络对评论函数进行参数化，然后使能量距离最大化。类似于MMD GAN，Cramér GAN对实现稳定学习的关键功能施加了Lipschitz约束。相比之下，为了避免Lipschitz约束，fisher GAN 与Sobolev GAN分别在Lebesgue球和Sobolev空间上定义了函数类。然而，它们需要在鉴别器中解决一个增加到拉格朗日函数以强制施行理论约束。

类似于MMD GAN与Fisher GAN，球形GAN把通过高阶统计学加工过的信息传入GAN物体识别功能区中。然而，MMD GAN与Fisher GAN若要满足理论假设需要大量的惩罚项。相比之下，球形GAN中的物体识别功能函数既简单又直接，而且足够健壮（容错率更高？），因为它在数学意义上等同于使用多维球体上定义的多个Wesserstein距离。在章节4中用数学证明了物体识别功能函数与IPM密切相关这一事实。

3.球形GAN

本章节介绍新颖的球形GAN以及它相较于基于IPM的GAN及其变种的一系列优点。

3.1物体识别功能函数

该函数基于Wasserstein度量直接匹配一维空间的“第一维”，公式如下所示。

其中G和D分别表示生成器和鉴别器，P和N分别表示真实数据和潜在代码分布。 在（1）中，鉴别符D将数据x映射到实数R

             D:

其中D应该满足1-Lipschitz条件 ，而 是n维欧几里得图像空间。 与传统的基于IPM的GAN一样，我们的GAN球体的物体识别函数基于公式（1）。

图1球体GAN工作流程

假数据是由发生器从噪点输入生成的，然后将真实数据与假数据传入鉴别器，该鉴别器将输出映射到n维欧几里得特征空间（即黄色平面）。平面上的绿色和紫色圆圈分别表示伪样本和真实样本的特征点。 通过几何变换，将这些特征点重新映射到n维球体（即黄色球）中。 通过使用这些映射点，球体GAN可以计算以多维球面北极为中心的几何矩。球形GAN的鉴别符试图令真实样本与假样本之间的概率度量的矩差最大，而生成器则试图通过使矩差最小化来干扰鉴别符。通过使用多维球体上定义几何距，生成器与鉴别器通过两者互相制衡（“two-player minmax game.  ”我认为应翻译如此）来达到增强性能的目的。

与现有的直接匹配一维特征空间的一阶矩的GAN不同，球形GAN匹配多维球体上定义的高阶矩和和多个矩。因此，鉴别器n维的多维球体：

                      D:

球形GAN的物体识别功能的数学公式如下

对于r = 1,…,R,在公式（8）中的函数项 描述的是每个多维球体样本的“北极点”之间的第r个矩距离。提示：下标s是表示 是在 上定义的。图一描述了球形GAN的工作流程。

根据公式（4）中描述的新功能函数，球形GAN显现出了几个优点。首先，通过在多维球体上定义IPM，可以减轻施加在鉴别器上的几个约束条件。如上所述，基于Wesserstein距离的传统判别器需要利普希茨约束，这迫使判别器成为1-Lipschitz函数模型的一部分。然而错误的权重参数 约束会显著降低学习网络的容量并且会（overly reflect sampled points ：过度反射采样点？？？）。例如，WGAN-GP、WGAN-CT和WGAN-LP在物体识别功能函数中需要额外的约束条件来更新鉴别器：

表1. 基于Wasserstein距离的常规GAN中使用的梯度罚分项

	额外约束条件
GP	]
CT	GP+
LP

P、CT与LP分别表示梯度惩罚，软件一致性（soft consistency）与利普希茨惩罚项 表示真实数据点到虚假数据点两者之间的连线上均匀采样的特征点。 , 表示受到丢失单元干扰的虚拟数据点。G*所在的位置表示固定的生成器，C表示由表1定义的其他额外的惩罚项。在公式（5）中梯度的基准因项目而异，计算它的步骤极为繁杂。球形GAN与众不同的是它无需额外的约束条件即可将鉴别器导入所需的功能空间中。通过几何变换，从而确保球形GAN中的距离函数放置在正确的功能空间中。于是我们用于更改鉴别器权重的新函数是无需额外约束项的

算法1表现了球形GAN的伪代码

3.2多维球体

与公式（4）中相同，球形GAN在多维球体  上定义的特征空间匹配多个矩。球形GAN使用多维球体来代替任意黎曼流形方程项 ，这么做有三个优点

1. 多维球体的距离项 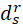有界而且变得易于实现
2. 梯度基数在距离函数中表现正常，这是稳定学习的关键
3. 多维球体的黎曼结构适用于定义GAN的目标物体

传统的GAN通常考虑欧几里得空间与欧几里得距离。这些GAN可以以任意黎曼流形方程为扩展。这些方程并非收敛所有它们是无界的，这就可能导致梯度基数溢出以及学习的不稳定。为了克服这一缺陷，球形GAN使用几何感知转换函数，把欧几里得空间的转换到多维球体的。注意该功能至少通过大量多个判别器加工才能生效。我们的转换函数通过“微分同构”（微分同构是双向且可微分的，它保留域和图像平滑流形切线的空间正切维数）来把 转换到 。从而，转换函数可以微分并且可以保存特征空间每个点的维度。下一章节将介绍在几何转换函数在的立体物件投影。

图2

欧几里得球面 的反向球极平面投影：

每条红线表示 与 的测地线。

3.3几何感应转换函数

该反向球极平面投影是欧几里得空间 到 多维球体的微分同胚。简单来说，反向球极平面投影可以说是多维平面投影到多维球体。 为坐标系， 为多维球体的北极,于是，欧几里得球面 的反向球极平面投影： 为如下定义：

在此反向球极平面投影公式中 ，以多维球体为度量，可测出这两点公式为

其中是 在 上定义的距离函数。

从几何意义上说， 可以被认为是测地线的长度。如图2所示，在多维球体上两点之间的测地线距离要比欧几里得距离更短，这使得它在多维球体上有界（就是黄色球体），因此实施几何转换等于对多维平面施加全局几何约束。在使用基于公式（4）的球形GAN的物体识别功能就可以达到稳定学习的目的。

引理1：公式（8）中的距离函数是有界且可微分的。

在公式（8）中的距离函数是满足非负且对称的，并且满足三角形不等式并且可以微分。由于多维球体是一个紧流形，所以任意两点之间的距离有界。例如，两点之间的欧几里得距离O=（0,…,0）、q=(t,…,t)偏离度： 并且 。相比之下，公式（8）中多维球体上定义的距离是收敛的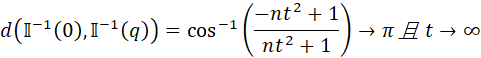： 。球形GAN上的几何转换感应功能颗粒让鉴别器输出的分布散度有界，从而确保稳定的学习。此外，该功能保留了特征空间的维数并保持了可区分性。

4.对于球形GAN的分析

本章节将从数学的角度分析球形GAN。

4.1与IPM的联系

我们首先证明最小化（4）中的目标函数等于最小化IPM。为了达到这个目的，我们在黎曼流形中定义几何中心矩。令 为紧凑的，可连通且短程的具有波莱尔 代数 的黎曼流形。每个 和 的概率测度皆定义在可测量空间（  ）上。于是IPM的定义如下：

定义1：IPM是两个概率度量 之间的距离度量：

F是  上的一类实值且有界的可测量函数

定义2：给定点 的  在（ ,  ）上的第r个中心矩为

其中  且  ,  为  上的黎曼距离函数。

在球形GAN中，我们在  中定义了新的IPM：

定义3：基于力矩差的IPM为

其中  是从给定点  到  上的另一个点

当我们拿定义1与定义3对比，即可得出常规IPM与球形GAN中的IPM之间的联系。当公式（11）中的 与公式（4）中的 相对应时， 可以被  所替代，  可以被设为北极N。然后，我们得到了一个类似于方程（4）的方程，这意味着最小化方程（4）中的目标函数等同于最小化方程（11）中的IPM。

然而，传统的IPM与球形GAN中的IPM仍有些许的不同。我们的IPM的函数空间是设立在  上以 ， 为中心的有界距离函数集。因此球形GAN的参数化距离方程为：

公式中{  }是图像集数。相比之下，IPM中的WGAN的功能空间是1-利普希茨鉴别器的集合。因此对鉴别器参数化的结果是

其中

4.2与Wesserstein距离的联系

  由球形GAN中的IPM在公式（11）中定义。球形GAN中的引擎目的是为了减少  的出现，这等效于匹配在  上定义的两个概率测度  与  之间的高阶中心矩：

命题1：当  逐渐减小向  收敛时

.

.对于所有的r而言：

令 为 上所定义的概率测度的r -Wesserstein距离时,最小化  等效于最小化所有r上的r-Wesserstein距离之和。

命题2：当 无限逼近，收敛至0时

由于弱收敛与Wasserstein距离密切相关，所以得到命题2的结果不足为奇。在常规的基于Wesserstein距离的GAN中，依据坎托罗维奇-鲁宾斯坦对偶定理，目标函数将被设计为对偶形式。在对偶形态下，仅有1-Wesserstein距离可以实现GAN的有效学习。与传统GAN相反，球形GAN可以使用普遍适用r-Wesserstein距离，因此，球形GAN拥有更宽泛的功能空间。

4.3梯度分析

由于比其他的IPM适用了更多的“ ”，球形GAN可以通过选择“ ”的不同矩来计算损失函数的梯度。当梯度不同时，选择不同的时刻会导致软件不同的学习行为。我们发现在任意时刻选择球形GAN都可以达到稳定学习的目的

命题2：对于任意 , 成立

命题2说明了使用多维球体是令GAN得以稳定学习的缘由，在训练过程中梯度系数是有界的。因为无需对判别器强加额外的惩罚项，所以我们的球形GAN可以设立非常大的梯度。因此会有梯度溢出的风险。然而，在实践中，我们证实在使用Adam优化程序时每次迭代的梯度系数的平均大小是可以承受的。

5.实验

5.1实验细节

超参数：网络经过每次64大小的训练（我没明白这句话…“64”是指文件大小吗，还是位数？）。在所有实验中，我们为将生成器与鉴别器的Adam优化器的超参数固定为 。在实验中使用的ConvNet我们将力矩设定为13dr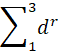 , 在传统的基于IPM的GAN中，鉴别器会多次更新，生成器每次迭代都会更新一次。与这些常规的GAN相反，在球形GAN在每个网络在每次迭代中都会被更新（我们的实践已经正式GAN学习的动力所在，然而这种影响因素难以直接比较和分析）。

几何区块：我们在几何感知转换功能中为卷积层添加了几何区块。判别器（D）与几何区块（GB）设置如下

其中， 为输入，ISGP则表示逆向立体投影，附加说明中提供了ISGP的伪代码以及其详细的网络结构。

基准网络：我们分别在两个基准网络ConvNet与ResNet中进行无人工干预的图片训练任务且我们遵循[20]中提出的网络架构来构建生成器和鉴别器。基准网络由生成器中的转换卷积块与鉴别器中的卷积块组成，其中每个卷积块由两个卷积层组成。我们遵循由公式【9】提出的网络架构来构建ResNet。在每个鉴别器网络中，我们依据【22】中把每个单元常规化，从而达到常规化层级的目的，并且我们为几何转换功能的最后的卷积块附加上几何块GB。关于网络的详细构造请查阅附加说明。

环境：所有实验均在装配有单块泰坦等级的Nvidia GTX图像处理器的机器中进行。球形GAN依赖于Tensorflow-1.11.0及Keras-2.2.4后端。

5.2数据集与评估指标

数据集：我们在CIFAR-10[13]、STL-10[6]以及LSUN[38]数据集中进行试验。CIFAR-10和STL-10数据集中含有50k（32x32像素）与100k（96x96像素）大小的10组不同的自然图片。我们为STL-10数据集提供48x48像素的缩小版的原始图片，为LSUN我们使用了三百万张64x64像素的卧室图片。

评估指标：为了平均网络的任务量，我们使用了起始分数（IS）与弗雷歇起始距离（FID）两项指标。我们通过这两项指标对球形GAN与其他基于IPM的GAN在各种数据集的表现进行评定。在所有的实验环境中，我们将以IS与FID两项指标，生产50k大小的图像来评估GAN。我们以作者源代码来进行评估。IS与人类的判断力以及启蒙能力更为相似。生成的图像将被应用于初始卷积网络【29】来获得条件分布 ，并且IS将被如下步骤计算： 并且 将由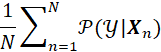 近似计算得到。另一方面，FID通过预估（？？？）克服了IS的缺陷（初始模型pool3）。FID与人类似，会受到不断增加的干扰。两个图像分布  之间的FID定义如下：

其中mi 和Ci 分别是从Pi 获得的高斯均值和协方差矩阵。

5.3控制变量研究（应该是这个意思）

本章节是为了回答以下三个问题

 

 

 

 

 

 

使用ConvNet在不同的矩匹配模式及多维球面的不同维度情况下在CIFAR-10数据集中的初始得分（IS）。红、黄、蓝条分别表示 、 和  三种不同的力矩模式。横轴表示多维球面的维度 。

 

 

 

图4球形GAN与WGAN-GP判别器网络的梯度基数

问题 1：应用更高的力矩来训练GAN是否会提高训练样本的质量？

 

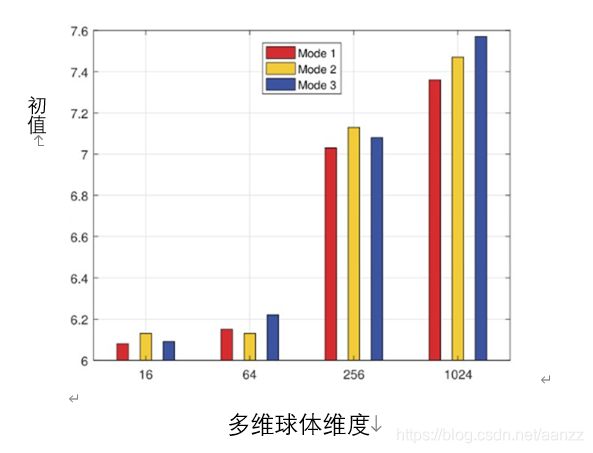
问题2：使用更高维度的多维度球体来训练GAN是否可以提高性能？

问题3：梯度基数在训练过程中表现是否正常？

答1：我们应用不同的力矩来进行无人工干预的图像生成任务证实了更高的力矩可以提升性能。在此次试验中，GAN功能使用了各种求和模式。如图3所示，在特征空间匹配更高的力矩显著地提高了性能。我们看到在CIFAR-10数据集中高于5阶的力矩会令性能遭受损失并且可能会导致学习的不稳定。然而在实验中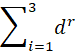 通常适用于大型网络。基于Wesserstein距离的传统GAN在更高阶的力矩中精度并没有得到提升。

 

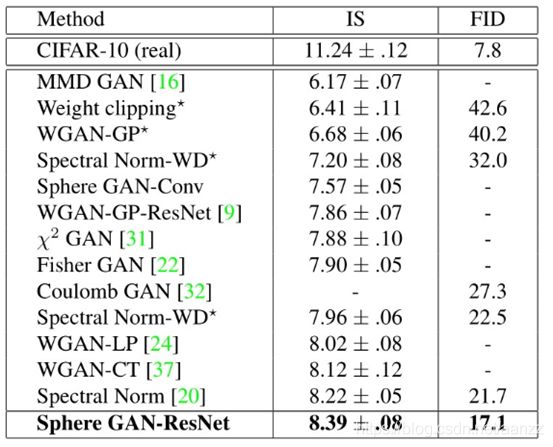
表2：CIFAR-10的无人工干预的图像生成结果 IS：越高越好 FID：越低越好 被“*”标记的网络，我们使用了【20】中的报告结果

 

答2：我们观察到在使用几何矩是多位球体的维数应该足够大到确保特征空间所包含的信息是有意义的。在如Wesserstein距离等其他方法中，特征空间是一维的，特征空间的维度数过低以至于无法把信息传入高阶统计中加工。在图3可证明更高维度的多维球体可以显著地提高球形GAN的精度。

答3：我们评估了每次迭代的梯度基数发现使用上文建议的指标可以稳定地训练GAN。如图4所示，梯度基数在十万次迭代之后开始收敛，而WGAN-GP很容易就达到收敛。在球形GAN中梯度基数与上文提到的指标近似（应该译为近似）

5.4 定量与定性的结果

CIFAR-10：表2总结了定量的成果。球形GAN在所有的IS和FID指标中均取得了最高分并遥遥领先。球形GAN-Conv也领先了WGAN-GP与MMD GAN。

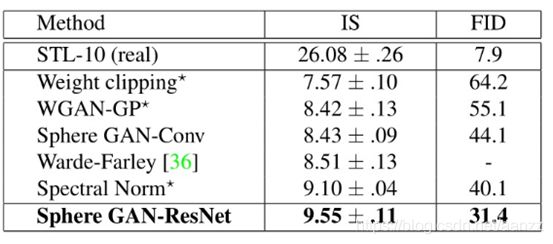
STL-10：在STL-10的实验中，相比于【20】中使用的原始网络，我们使用了大约一半的网络参数。从图3可看出，即使是在小网络参数的环境下，球形GAN-ResNet仍然明显地超越SN-GAN以及其他基于IPM的GAN。

LSUN卧室：如【4】中所述，在此次试验中我们只报告了FID因为IS是无意义的。表4表面球形GAN-ResNet显著优于最新的GAN。

 

表3：STL-10的无人工干预的图像生成结果 被“*”标记的网络，我们使用了【20】中的报告结果

 

 

表4：LSUN卧室的无人工干预的图像生成结果 被“*”标记的网络，我们使用了【4】中的报告结果

 

 

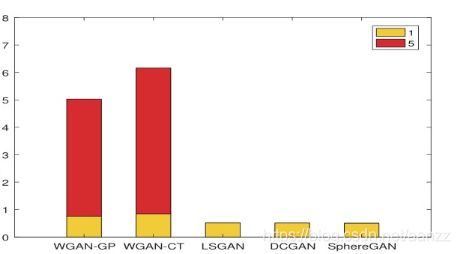
100次迭代的平均用时

 

 

 

 

图5.不同种类的GAN超过100次迭代的平均计算用时 黄条和红条分别代表生成器与鉴别器更新率为1:1与1:5时的平均计算时间

 

训练用时：在图5我们计算了不同方法超过第100次迭代的平均用时。由于每次迭代都要计算梯度基数||∇xDx||2 ,WGAN-CT与WGAN-GP明显比其他方法要缓慢（比DCGAN慢了40%）。球形GAN明显比其他基于IPM的GAN用时更少，几乎与DCGAN【25】和LSGAN【18】一样快。

我们使用了三个数据集对球形GAN做了定性评估。图6、7分别展现了LSUN卧室和STL-10数据集对球形GAN定性评估的结果。定性评估的结果表明球形GAN可以稳定地训练且极少出现模组崩溃的问题。大多数生成的图像极为逼真。

6.结论

本论文提出来一个名为球形GAN的新型的基于IPM的GAN。球形GAN在多维球体（一种黎曼流形）上定义IPM，一次可以在有界的IPM上稳定地训练。高阶矩匹配令球形GAN得以高效地利用数据集中的有效数据并得到精确的结果。实验证明在LSUN、STL-10以及CIFAR-10数据集中球形GAN相较于基于IPM的GAN都展现了优异的性能

图6：球形GAN在LSUN卧室数据集的定性结果

图7：球形GAN在STL-10数据集在的定性结果

致谢

本研究得到了韩国政府（MSIT）的信息和通信技术规划与评估研究所（IITP）资助（No.2017-0-01780）。

参考文献：

……(这就不用翻译了吧？)