JDK1.8 ArrayDeque源码阅读
概述
ArrayDeque是一个数组实现的双端队列,它不是线程安全的,并且不允许操作null值,把他当做栈使用时,要比Stack(Stack是线程安全的,使用synchronized修饰方法)更高效,当队列使用时,要比LinkedList(使用链表实现)更高效。
结构
在看ArrayDeque的源码前,先要了解循环数组。
如果用数组实现队列的话,可能的实现方式:

当把元素入队时,tail(队尾元素的下标)加一。
当出队时,head(队头元素的下标)加一。
那么当队尾已经达到数组的尾部时而队头不在数组的头部时,此时入队的话,要么搬移数组的元素,重新把数组内的元素搬移到从数组头开始,这个操作的时间复杂度是O(n)。还有一种做法就是把入队的元素存储在head前的空置位置。例如:
这就是循环数组的做法。
入队出队时,head跟tail的计算方法如下:
- 当入队时,tail = (tail + 1) % array.length
- 当出队时,head = (head + 1) % array.length
当tail = head时,队列为空。
当(tail + 1) % array.length = head时,队列已满。
下面看ArrayDeque对应的字段:
/**
* 不设置私有以简化嵌套类的访问
* 因为private域只有本类能访问,所以为了使嵌套类能访问到private域,JVM需要生成额外的getter方法。
*/
transient Object[] elements;
/**
* 标记队头下标,当head==tail时,队列为空。
*/
transient int head;
/**
* 标记队尾下标。
*/
transient int tail;
方法
在ArrayDeque中,数组的长度一直为2的N次方(为了tail跟head的计算),代码如下:
/**
* 最小容量
*/
private static final int MIN_INITIAL_CAPACITY = 8;
/**
* 获得2的N次方
*/
private static int calculateSize(int numElements) {
int initialCapacity = MIN_INITIAL_CAPACITY;
/**
* 在java中,int类型占4个字节,也就是32位,例如0100 0000 0000 0000 0000 0000 0000 0000
* 逻辑右移1位,并且进行或操作,可得0110 0000 0000 0000 0000 0000 0000 0000
* 逻辑右移2位,并且进行或操作,可得0111 1000 0000 0000 0000 0000 0000 0000
* 逻辑右移4位,并且进行或操作,可得0111 1111 1000 0000 0000 0000 0000 0000
* 逻辑右移8位,并且进行或操作,可得0111 1111 1111 1111 1000 0000 0000 0000
* 逻辑右移16位,并且进行或操作,可得0111 1111 1111 1111 1111 1111 1111 1111
* 然后加1得1000 0000 0000 0000 0000 0000 0000 0000
* 通过计算后可得比numElements大的最小2的N次方。
*/
if (numElements >= initialCapacity) {
initialCapacity = numElements;
initialCapacity |= (initialCapacity >>> 1);
initialCapacity |= (initialCapacity >>> 2);
initialCapacity |= (initialCapacity >>> 4);
initialCapacity |= (initialCapacity >>> 8);
initialCapacity |= (initialCapacity >>> 16);
initialCapacity++;
/**
* 是否溢出,当溢出时,该数为-2147483648,也就是
* 10000000000000000000000000000000
*/
if (initialCapacity < 0)
initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
}
return initialCapacity;
}
addFirst
把元素插入到队列头部
public void addFirst(E e) {
if (e == null)
throw new NullPointerException();
/**
* 计算head的下标,如果我们不考虑边界,那么head = head - 1,
* 但是实际上当head = 0时,我们插入元素到队列的头部,
* head的值应该存储在数组的尾部,但是这里不能使用(head - 1) % (elements.length - 1),
* 把数组长度设计为2的N次方,可以减少判断,而且位运算要更快
*/
elements[head = (head - 1) & (elements.length - 1)] = e;
if (head == tail)
doubleCapacity();
}
我们来看一下head = (head - 1) & (elements.length - 1)怎么计算出head的。
因为数组的长度为2的N次方,那么elements.length - 1的二进制位低位全1,如:
数组长度为8,那么这个数为0000 0000 0000 0000 0000 0000 0000 0111,所以该数与任何数&的结果都会比数组的长度小,相当于一个低位掩码。
那么任何数与elements.length - 1进行与运算都相当于截取低n( 2 n 2^n 2n的n)位,所以正整数与elements.length - 1进行与运算相当于取模。
负整数则不一样,由于负数在计算机中采用补码表示,也就是其原码取反加一,那么负整数与elements.length - 1进行与运算,相当于 2 n − 1 + 该 负 数 + 1 2^n - 1 + 该负数 + 1 2n−1+该负数+1,再与elements.length取模,这里的n是比该负数的绝对值大的最小的( 2 n − 1 2^n - 1 2n−1)的位数。如果该负数的绝对值小于等于数组的长度,那么相当于(该负数)+ elements.length。
在循环数组中,把head分为两种情况:
当head > 0,所以head - 1 > 0,那么(head - 1) & (elements.length - 1) = head - 1。
当head = 0, 所以head - 1 = -1,那么(head - 1) & (elements.length - 1) = elements.length - 1。
计算出head后,把元素存储在该位置。
检查数组是否已满(head == tail),是否需要进行扩容。

private void doubleCapacity() {
assert head == tail;
int p = head;
int n = elements.length;
/**
* 计算从head到数组尾部的元素数量
*/
int r = n - p;
int newCapacity = n << 1;
if (newCapacity < 0)
throw new IllegalStateException("Sorry, deque too big");
Object[] a = new Object[newCapacity];
/**
* 搬移从head到数组尾部的元素
* 搬移从数组头部到tail的元素
*/
System.arraycopy(elements, p, a, 0, r);
System.arraycopy(elements, 0, a, r, p);
elements = a;
head = 0;
tail = n;
}
扩容过程如下图:
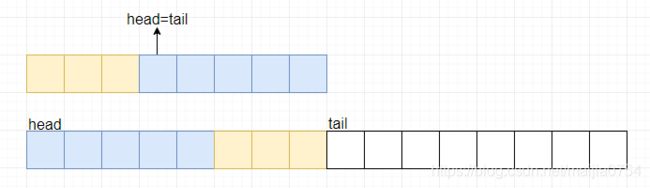
弄明白这个过程,ArrayDeque中的很多方法都与addFirst的分析过程类似。
removeFirstOccurrence
/**
* 移除第一个匹配的元素
*/
public boolean removeFirstOccurrence(Object o) {
if (o == null)
return false;
int mask = elements.length - 1;
int i = head;
Object x;
/**
* 遍历队列里的每一个元素
*/
while ( (x = elements[i]) != null) {
if (o.equals(x)) {
delete(i);
return true;
}
i = (i + 1) & mask;
}
return false;
}
private void checkInvariants() {
//循环数组的tail不存储元素
assert elements[tail] == null;
//如果数组为空,那么elements[head]为空
//如果数组不为空,那么tail的前一个位置必定存储元素
assert head == tail ? elements[head] == null :
(elements[head] != null &&
elements[(tail - 1) & (elements.length - 1)] != null);
//head的前一个位置必定没有存储元素
assert elements[(head - 1) & (elements.length - 1)] == null;
}
/**
* 删除元素,i是待删除元素的下标
* @return 搬移从i到tail的元素返回true,搬移从head到i的元素则返回false
* 这是因为在迭代器中调用到此方法,需要靠此返回值来判断是否取消next指针的增量
*/
private boolean delete(int i) {
//检查是否符合循环数组的特征
checkInvariants();
final Object[] elements = this.elements;
final int mask = elements.length - 1;
final int h = head;
final int t = tail;
//i到head之间有多少个元素
final int front = (i - h) & mask;
//tail到i之间有多少个元素(tail不存储元素,所以会多1)
final int back = (t - i) & mask;
//必须存在head <= i < tail
if (front >= ((t - h) & mask))
throw new ConcurrentModificationException();
//如果前面的数据量少,则搬移前面的元素,以获得更好的性能
if (front < back) {
//如果h <= i,那么head到i之间没有越过数组的头部(下标0)
if (h <= i) {
System.arraycopy(elements, h, elements, h + 1, front);
} else { //越过数组的头部(下标0)
//先搬移从数组头部开始的部分
System.arraycopy(elements, 0, elements, 1, i);
//把数组尾部的元素放到数组头部
elements[0] = elements[mask];
//搬移剩下的元素
System.arraycopy(elements, h, elements, h + 1, mask - h);
}
//因为搬移前面的数据,所以整体往后移
//此时指定元素已经删除,但是head位置元素重复,所以让elements[h] = null
elements[h] = null;
//重新计算head
head = (h + 1) & mask;
return false;
} else { //后面数据量少,搬移后面的数据,元素前移
if (i < t) {
//back会比实际数量多1,所以会复制null的tail
System.arraycopy(elements, i + 1, elements, i, back);
tail = t - 1;
} else { // Wrap around
System.arraycopy(elements, i + 1, elements, i, mask - i);
elements[mask] = elements[0];
System.arraycopy(elements, 1, elements, 0, t);
tail = (t - 1) & mask;
}
return true;
}
}
在ArrayDeque中运用了很多的位运算,通过阅读源码,可以使我们跟熟悉位运算与其应用,也可以学习循环数组与其实现。


