蓝桥杯c++B组练手（一）

题目摘自：https://blog.csdn.net/u014552756/article/details/50577232
1.

微生物增殖
假设有两种微生物 X 和 Y
X出生后每隔3分钟分裂一次（数目加倍），Y出生后每隔2分钟分裂一次（数目加倍）。
一个新出生的X，半分钟之后吃掉1个Y，并且，从此开始，每隔1分钟吃1个Y。
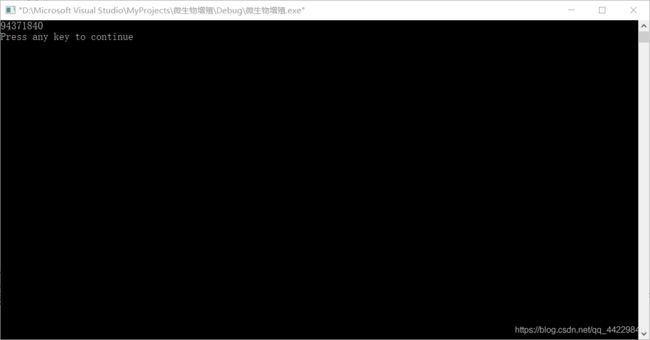
现在已知有新出生的 X=10, Y=89，求60分钟后Y的数目。
如果X=10，Y=90呢？
本题的要求就是写出这两种初始条件下，60分钟后Y的数目。
题目的结果令你震惊吗？这不是简单的数字游戏！真实的生物圈有着同样脆弱的性质！也许因为你消灭的那只 Y 就是最终导致 Y 种群灭绝的最后一根稻草

陷阱：y被吃完

#include
using namespace std;
int main(){
     
 int x=10,y=90;
 for(int i=1;i<=120;i++)
 {
     
  if(i%2==1&&y>=x)//每到半分钟时，x吃y，无论是新生的x还是老的x都在这个判断中吃，而且前提是此时y够x吃
  {
     
  y=y-x;
  }
  if(i%2==1&&y<x)//到x吃y时，此时y不够吃，y直接变为0且跳出循环
  {
     
  y=0;
  break;
  }
  if(i%4==0){
     //2分钟y加倍
  y=y*2;
  }
  if(i%6==0)//3分钟x加倍
  {
     
  x=x*2;
  }
 }
 cout<<y<<endl;
 return 0;
} 

输出结果
当x=10，y=89

当x=10，y=90

2.

古堡算式
福尔摩斯到某古堡探险，看到门上写着一个奇怪的算式：
ABCDE * ? = EDCBA
他对华生说：“ABCDE应该代表不同的数字，问号也代表某个数字！”华生：“我猜也是！”于是，两人沉默了好久，还是没有算出合适的结果来。请你利用计算机的优势，找到破解的答案。把 ABCDE 所代表的数字写出来。思路：循环遍历每个字母可能的情况。

难点：代表不同的数字时用continue跳出循环

# include 
#in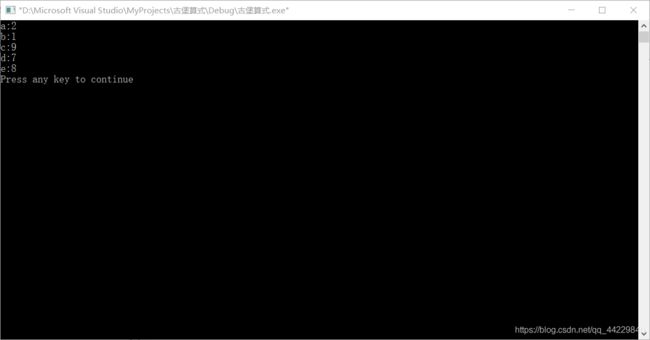clude
using namespace std;
int main()
{
     
 int a, b, c, d, e;
 int x; 
 int m, n;
 for(a = 0; a <= 9; a++){
      
  for(b = 0; b <= 9; b++){
     
   if(a == b) {
      
    continue; 
  }  
   for(c = 0; c <= 9; c++){
     
    if(c == a || c == b) {
     
     continue; 
   } 
    for(d = 0; d <= 9; d++){
     
     if(d == a || d == b || d == c) {
     
      continue; 
    }   
     for(e = 0; e <= 9; e++){
     
      if(e == a || e == b || e == c || e == d) {
      
       continue;   
   }     
      for(x = 0; x <= 9; x++){
     
       m = a * 10000 + b * 1000 + c * 100 + d * 10 + e * 1; 
       n = e * 10000 + d * 1000 + c * 100 + b * 10 + a * 1;
       if(m * x == n){
       
        cout<<"a:"<<a<<endl;
        cout<<"b:"<<b<<endl;
        cout<<"c:"<<c<<endl;
        cout<<"d:"<<d<<endl;
        cout<<"e:"<<e<<endl;
      }   
   }   
  }  
  } 
  }
  }
 }
 return 0;
}

输出：
为什么不用if a!=b则进入下个循环的方式：因为这样输出结果时需要跳出多个循环，很不方便；

海盗比酒量
有一群海盗（不多于20人），在船上比拼酒量。过程如下：
打开一瓶酒，所有在场的人平分喝下，有几个人倒下了。再打开一瓶酒平分，又有倒下的，再次重复… 直到开了第4瓶酒，坐着的已经所剩无几，海盗船长也在其中。当第4瓶酒平分喝下后，大家都倒下了。
等船长醒来，发现海盗船搁浅了。他在航海日志中写到：“…昨天，我正好喝了一瓶…奉劝大家，开船不喝酒，喝酒别开船…”
请你根据这些信息，推断开始有多少人，每一轮喝下来还剩多少人。
如果有多个可能的答案，请列出所有答案，每个答案占一行。
格式是：人数,人数,…例如,有一种可能是：20,5,4,2,0
思路：4次之后船长喝了1瓶，每一次喝的量都是一个分数，4次之和为1

如果每轮都必须有人倒下：
（如果每轮可以没有人倒下则有更多的可能解）

#include
#include
using namespace std;
int main(){
     
 int x,a,b,c;
 for(x=20;x>0;x--){
     
  for(a=1;a<x;a++){
     
   for(b=1;b<x-a;b++){
     
    for(c=1;c<x-a-b;c++){
     
     if((x-a-b-c)*(x-a-b)*(x-a)+(x-a-b-c)*(x-a-b)*x+(x-a-b-c)*(x-a)*x+(x-a-b)*(x-a)*x==(x-a-b-c)*(x-a-b)*(x-a)*x){
     
      cout<<x<<","<<x-a<<","<<x-a-b<<","<<x-a-b-c<<","<<"0"<<endl;
     }
    }
   }
  }
 }
 return 0;
}

输出：

4.

奇怪的比赛
某电视台举办了低碳生活大奖赛。题目的计分规则相当奇怪：
每位选手需要回答10个问题（其编号为1到10），越后面越有难度。答对的，当前分数翻倍；答错了则扣掉与题号相同的分数（选手必须回答问题，不回答按错误处理）。
每位选手都有一个起步的分数为10分。
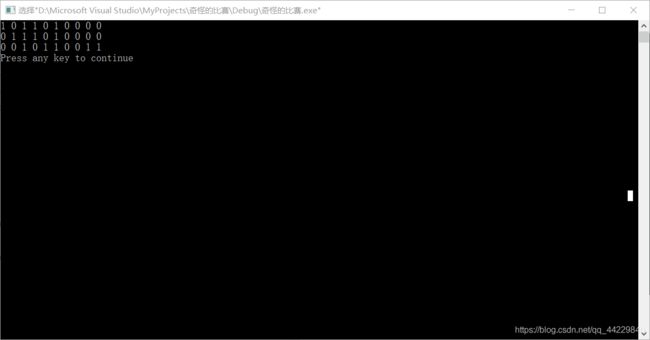
某获胜选手最终得分刚好是100分，如果不让你看比赛过程，你能推断出他（她）哪个题目答对了，哪个题目答错了吗？
如果把答对的记为1，答错的记为0，则10个题目的回答情况可以用仅含有1和0的串来表示。
例如：0010110011 就是可能的情况。你的任务是算出所有可能情况。
每个答案占一行。
思路：深搜

想到深搜就想到要用递归

#include
using namespace std;
int a[10];
void DFS(float score,int x){
     
 if(x==11&&score==100){
     
  for(int i=1;i<=10;i++)
   cout<<a[i-1]<<" ";
  cout<<endl;   
  return;  
 }
 if(x>11)
  return;
 a[x-1]=1;
 DFS(score*2,x+1);
 a[x-1]=0; 
 DFS(score-x,x+1);
}
int main(){
     
 DFS(10,1);
 return 0;
}

输出：

5.

高斯日记
大数学家高斯有个好习惯：无论如何都要记日记。
他的日记有个与众不同的地方，他从不注明年月日，而是用一个整数代替，比如：4210
后来人们知道，那个整数就是日期，它表示那一天是高斯出生后的第几天。这或许也是个好习惯，它时时刻刻提醒着主人：日子又过去一天，还有多少时光可以用于浪费呢？
高斯出生于：1777年4月30日。
在高斯发现的一个重要定理的日记上标注着：5343，因此可算出那天是：1791年12月15日。
高斯获得博士学位的那天日记上标着：8113
请你算出高斯获得博士学位的年月日。
提交答案的格式是：yyyy-mm-dd, 例如：1980-03-21

这个写法很妙：
高斯日记

填空题想要写完整代码好难，尤其是算年月日的题目特别棘手。。。
我老是想在一个主函数里完成所有东西

#include
using namespace std;
 int a[12] = {
     31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
 int b[12] = {
     31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
 int main(){
     
  int n=8113;
  int y=1777,m=4,d=30;
  int x1=n/1461;//1461为四年的循环
  int x2=n%1461;
  y=y+x1*4;
  if((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)&&x2>366) {
     
   x2=x2-366;
   y=y+1;
  }
  while(x2>366){
     
   if((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
     
   x2=x2-366;
   y=y+1;
  }
   else {
     
    x2=x2-365;
    y=y+1;
   }
  }
  cout<<x2<<endl;
  int sum=0;
  if((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
     
   for(int i=m;i<=11;i++){
     
    sum=sum+b[i];
   }
  }
   else{
     
    for(int j=m;j<=11;j++){
     
    sum=sum+a[j];
   }
   }
   cout<<sum<<endl;
   if(x2>=sum){
     
   x2=x2-sum;
   y=y+1;
   if((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
     
    for(int s3=0;s3<=11;s3++){
     
     if(x2>b[s3]){
     
      x2=x2-b[s3];
      m=m+1;
     }
      else{
     
      cout<<y<<"-"<<m<<"-"<<x2-1<<endl;
      break;
     }
    }
   }
   else{
     
    for(int s4=0;s4<=11;s4++){
     
     if(x2>a[s4]){
     
      x2=x2-a[s4];
      m=m+1;
     }
      else{
     
      cout<<y<<"-"<<m<<"-"<<x2-1<<endl;
      break;
     }
    }
   }
   }
   else{
     
   if((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
     
    for(int s1=m-1;s1<=11;s1++){
     
     if(x2>(b[s1]-d)){
     
      x2=x2-b[s1]+d;
      m=m+1;
      d=0;
     }
     else{
     
      cout<<y<<"-"<<m<<"-"<<x2-1<<endl;
      break;
     }
    }
   }
   else{
     
     for(int s2=m-1;s2<=11;s2++){
     
     if(x2>(a[s2]-d)){
     
      x2=x2-a[s2]+d;
      cout<<x2<<endl;
      m=m+1;
      d=0;
     }
     else{
     
      cout<<y<<"-"<<m<<"-"<<x2-1<<endl;
      break;
     }
    }
   }
   }
   return 0;
}

输出：

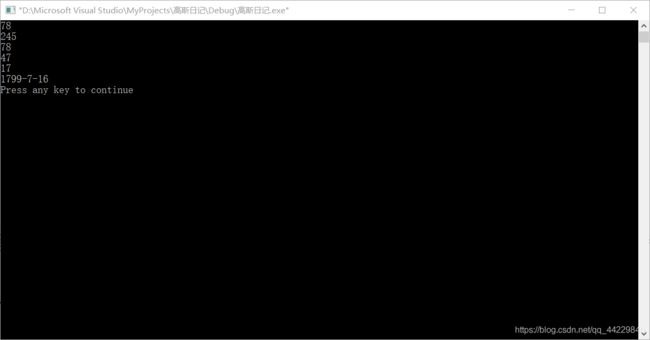
为了测试准确性输出了好多乱七八糟的，好歹是能算出正确结果了，不过这个代码没有什么算法性，完全是抠出来的答案，不好。

马虎的算式
小明是个急性子，上小学的时候经常把老师写在黑板上的题目抄错了。
有一次，老师出的题目是：36 x 495 = ?
他却给抄成了：396 x 45 = ?
但结果却很戏剧性，他的答案竟然是对的！！
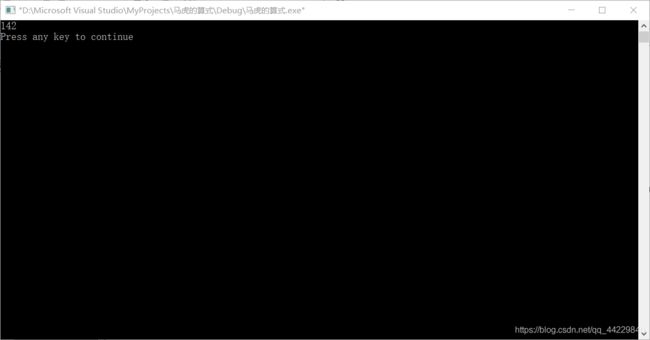
假设 a b c d e 代表1~9不同的5个数字（注意是各不相同的数字，且不含0）
能满足形如： ab * cde = adb * ce 这样的算式一共有多少种呢？
请你利用计算机的优势寻找所有的可能，并回答不同算式的种类数。
满足乘法交换律的算式计为不同的种类，所以答案肯定是个偶数。
因为 36 * 495 = 396 * 45 = 17820
类似这样的巧合情况可能还有很多，比如：27 * 594 = 297 * 54

#include 
using namespace std;
int main(){
     
 int a, b, c, d, e;
 int n = 0;
 for(a = 1; a < 10; a++) {
     
  for(b = 1; b < 10; b++) {
     
   if(a == b) {
     
    continue;
   }
   for(c = 1; c < 10; c++) {
     
    if(c == a || c == b) {
     
     continue;
    }
    for(d = 1; d < 10; d++) {
     
     if(d == c || d == b || d == a) {
     
      continue;
     }
     for(e = 1; e < 10; e++) {
     
      if(e == d || e == c || e == b || e == a) {
     
      continue;
      }
      if((a * 10 + b) * (c * 100 + d * 10 + e) == (a * 100 + d * 10 + b) * (c * 10 + e)) {
     
       n++;
      }
     }
    }
   }
  }
 }
 cout<<n<<endl;;
}

输出：

这一题跟古堡算式很像；

第39级台阶
小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!
站在台阶前，他突然又想着一个问题：
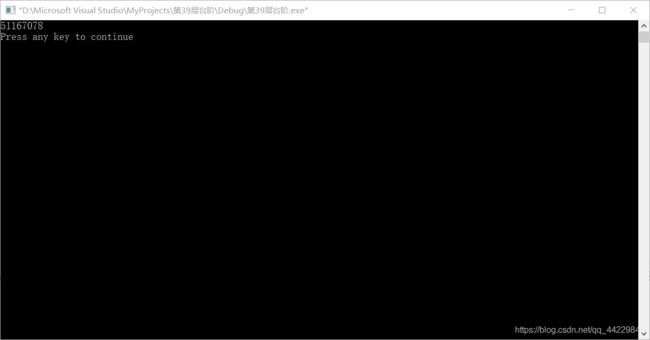
如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？
请你利用计算机的优势，帮助小明寻找答案。
思路：dfs深搜所有可能得情况。

这串代码是搬运的，主要是写的很精简，看完之后没有别的想写的念头了

#include 
using namespace std;
int sum;
void dfs(int n,int k)
{
     
    if(n>39) return;
    if(n==39&&k%2==0)
    {
     
        sum++;
        return;
    }
    dfs(n+1,k+1);
    dfs(n+2,k+1);
}
int main()
{
     
    sum=0;
    dfs(0,0);
    cout<<sum<<endl;
    return 0;
}

输出：

8.

黄金连分数
黄金分割数0.61803… 是个无理数，这个常数十分重要，在许多工程问题中会出现。有时需要把这个数字求得很精确。
对于某些精密工程，常数的精度很重要。也许你听说过哈勃太空望远镜，它首次升空后就发现了一处人工加工错误，对那样一个庞然大物，其实只是镜面加工时有比头发丝还细许多倍的一处错误而已，却使它成了“近视眼”!!
言归正传，我们如何求得黄金分割数的尽可能精确的值呢？有许多方法。
比较简单的一种是用连分数：
1
黄金数 = ---------------------
1
1 + -----------------
1
1 + -------------
1
1 + ---------
1 + …
这个连分数计算的“层数”越多，它的值越接近黄金分割数。
请你利用这一特性，求出黄金分割数的足够精确值，要求四舍五入到小数点后100位。
小数点后3位的值为：0.618
小数点后4位的值为：0.6180
小数点后5位的值为：0.61803
小数点后7位的值为：0.6180340
（注意尾部的0，不能忽略）
你的任务是：写出精确到小数点后100位精度的黄金分割值。
注意：尾数的四舍五入！ 尾数是0也要保留！
显然答案是一个小数，其小数点后有100位数字。
思路：斐波纳契数列和模拟手算除法实现

这一题不会水了：格式输出，题目理解和类型定义我都觉得我还不够
黄金连分数

#include
#include
#include
#define max(a,b)=?a>b
using namespace std;
//思路：由黄金连分数可转化为求解斐波那契数，运用大数运算求解小数点后一百位
//n表示斐波那契数列第一百项
int n = 100; 
int cmp(string a, string b)
{
     
 if (a == b) return 0;
 else if (a.length() < b.length()) return -1;
 else if (a.length() > b.length()) return 1;
 else
 {
     
  if (a > b) return 1;
  if (a < b) return -1;
  return -1;
 }
}
//大数相加，较大斐波那契数无法算出，只能通过大数计算
string add(string a, string b)
{
     
 //去掉开头的0,substr(a,n) 返回第a位开始长度为n的字符串
 //find_first_not_of（"abc"）返回最先匹配到abc任意一个字符的最后位置
 a = a.substr(a.find_first_not_of('0'));
 b = b.substr(a.find_first_not_of('0'));
 long long lenA = a.length();
 long long lenB = b.length();
 long long len = max(lenA, lenB) + 10;
 //反转， 便于从最低位逐位求和
 reverse(a.begin(), a.end());
 reverse(b.begin(), b.end());
 string ans(len, '0');
 for (int j = 0; j < lenA; j++)
 {
     
  ans[j] = a[j];
 }
 //通过模拟手工计算来进行大数相加，temp用来存储上下两位相加的结果
 int temp = 0;
 for (int i = 0; i < len; i++)
 {
     
  if (i < lenB)
  {
     
   temp += ((ans[i] - '0') + (b[i] - '0'));
   ans[i] = temp % 10 + '0';
   temp /= 10;
  }
  else
  {
     
   temp += (ans[i] - '0');
   ans[i] = temp % 10 + '0';
   temp /= 10;
  }
 }
 //ans存储的结果最后要反转回来去掉开头的0
 reverse(ans.begin(), ans.end());
 return ans.substr(ans.find_first_not_of('0'));
}
//大数相减
string substract(string a, string b)
{
     
 //a必须大于b,实际上在divide（）中，a已经>=b了
 reverse(a.begin(), a.end());
 reverse(b.begin(), b.end());
 //将a复制给ans
 string ans = a;
 //依旧是模拟手工减法计算
 for (int i = 0; i < b.length(); i++)
 {
     
  if (ans[i] >= b[i])
  {
     
   ans[i] = ans[i] - b[i] + '0';
  }
  //注意：在被减数不够减的情况下，需要向前借位，
  //可能被借位为0也不够借，继续往前寻找不为0的位，通过一个while循环实现
  else
  {
     
   int k = 1;
   while (ans[i + k] == '0')
   {
     
    //0被借位变为9
    ans[i + k] = '9';
    k++;
   }
   //最终i+k位不为0可以被借-1，i位+10
   ans[i + k] = ans[i + k] - 1;
   ans[i] = ans[i] + 10 - b[i] + '0';
  }
 }
 reverse(ans.begin(), ans.end());
 return ans.substr(ans.find_first_not_of('0'));
}
//大数相除
string divide(string a, string b)
{
     
 //前提 a < b 实际题目已满足
 //大数除法实际上是模拟除法运算结合大数减法
 string ans = "0.";
 for (int i = 0; i < 101; i++) //保留101项，保证四舍五入
 {
     
  // (a*10)/b = t 不过其中除法用减法substract代替
  a.append(1,'0');
  int t = 0;
  while (cmp(a, b) >= 0)
  {
     
   a = substract(a, b);
   t++;
  }
  ans.append(1,t + '0');
 }
 return ans;
}
int main()
{
     
 //斐波那契数列前两项
 string a = "1";
 string b = "1";
 for (int k = 0; k < 40; k++)
 {
     
  //求解斐波那契数列100-140各项与前一项的比值（所谓黄金连分数）
  for (int i = 3; i < n+k; i++)
  {
     
   string temp = b;
   b = add(a, b);
   a = temp;
  }
    string ans = divide(a, b);
  cout << 100+k  << "项  " <<ans << endl;
 }
 return 0;
}

本来想一次博客做一整套卷子的但是没想到看到卷子后面的代码填空和大题突然整个人都不好了所以能做多少就算多少吧，嘿嘿。
做这种竞赛题真的感觉自己算法学了个寂寞，代码完全是想到哪写到哪，每一题都得看看别人的，心好痛。