Android 绘图贝塞尔曲线简单使用
Android 绘图贝塞尔曲线简单使用
在Android中某些自定义View的时候需要绘制某些曲线,这时候贝塞尔曲线就登场了。
我们不用深入了解贝塞尔曲线的详细信息,我们的最终目的还是需要学会如何使用。贝塞尔曲线分为3种,分别为一阶贝塞尔曲线、二阶贝塞尔曲线、三阶贝塞尔曲线。
一阶贝塞尔曲线
一阶贝塞尔曲线是一条直线,只需要指定两个点就可以画出了,简单粗暴的使用就是:
canvas.drawLine(start.x,start.y,end.x,end.y);
二阶贝塞尔曲线:
二阶贝塞尔曲线的原理图是这样的:(图片取自网络)
![]()
由上图看,P0是起点,P2是终点。P1是控制点,t是一个系数,表示从0-1的变化过程,红色的线就是最终画出的曲线。然后说了这么多可能也没什么卵用。。
其实只要我们知道,我们指点了P1、P2、P3的坐标,即可实现画出上图中红色的曲线。具体的代码是如何的呢?
在Android中使用二阶贝萨尔曲线的函数是,Path对象的quadTo方法,如下。
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPaint.setColor(Color.RED); //画笔颜色
mPaint.setStrokeWidth(10); //画笔宽度
mPaint.setStyle(Paint.Style.STROKE);
mPath.reset();
//起点
mPath.moveTo(startPoint.x, startPoint.y);
//mPath
mPath.quadTo(assistPoint.x, assistPoint.y, endPoint.x, endPoint.y);
//画path
canvas.drawPath(mPath, mPaint);
//画控制点
canvas.drawPoint(assistPoint.x, assistPoint.y, mPaint);
//画线
canvas.drawLine(startPoint.x, startPoint.y, assistPoint.x, assistPoint.y, mPaint);
canvas.drawLine(endPoint.x, endPoint.y, assistPoint.x, assistPoint.y, mPaint);
}三阶贝塞尔曲线
三阶贝塞尔曲线和二阶的有限类似,不过是多了一个控制点,指定一个起点和一个终点,再指定两个控制点即可实现:
原理图(来自网络):
![]()
在Android中使用二阶贝萨尔曲线的函数是,Path对象的cubicTo方法,如下。
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPaint.setColor(Color.RED); //画笔颜色
mPaint.setStrokeWidth(10); //画笔宽度
mPaint.setStyle(Paint.Style.STROKE);
mPath.reset();
//起点
mPath.moveTo(startPoint.x, startPoint.y);
//mPath
mPath.cubicTo(assistPoint1.x, assistPoint1.y, assistPoint2.x, assistPoint2.y, endPoint.x, endPoint.y);
//画path
canvas.drawPath(mPath, mPaint);
//画控制点
canvas.drawPoint(assistPoint1.x, assistPoint1.y, mPaint);
canvas.drawPoint(assistPoint2.x, assistPoint2.y, mPaint);
//画线
canvas.drawLine(startPoint.x, startPoint.y, assistPoint1.x, assistPoint1.y, mPaint);
canvas.drawLine(endPoint.x, endPoint.y, assistPoint2.x, assistPoint2.y, mPaint);
canvas.drawLine(assistPoint1.x, assistPoint1.y, assistPoint2.x, assistPoint2.y, mPaint);
}
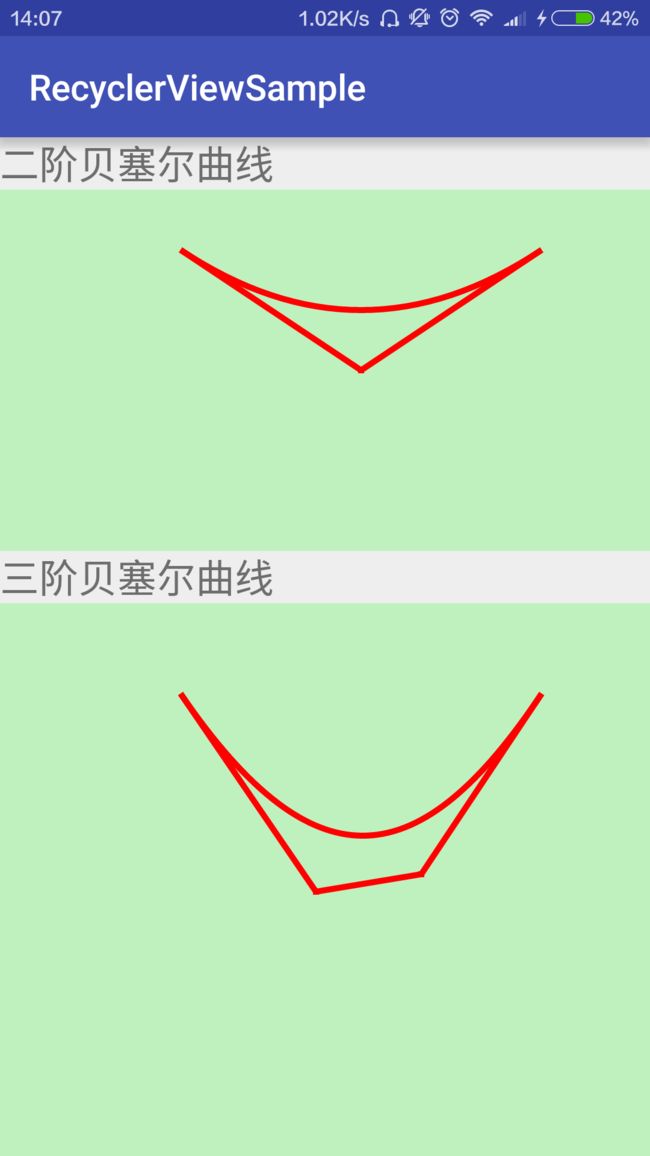
整体的效果运行图如下:
拓展使用
知道贝塞尔曲线的使用除了在自定义View中利用Path对象画曲线之外还有一些其他的运用,比如在设置动画的路径的时候。这通常能实现某些炫酷的效果。不过这种场景就没有封装好的方法来利用了,需要通过公式自己计算。下面是一些贝塞尔曲线的公式:
二阶贝塞尔曲线公式:
![]()
三阶贝塞尔曲线公式:
![]()
t的值是由0-1变化的,对于Android上面的动画来说,这个值不难获得,然后最终的x坐标和y坐标都通过这个公式获取即可,这样的出来的点的路径就是贝塞尔曲线的路径。
源码地址:http://www.jianshu.com/writer#/notebooks/4366188/notes/4763603