多项式全家桶——Part.4 多项式ln、exp、快速幂
拿头学真的学得会!
咕咕咕了好久,它又回来了。
其实最近一直在补补微积分的东东,算是一个初步入门了吧。
要学微积分可以康百度百科
或者看这位大佬的总结:戳这里!
然后多项式要求ln、exp、快速幂之类的神奇操作其实只需要用到少许的知识,下面小结一下。
前置芝士1:微积分
导数
导数是一个线性近似(或线性接近)的一个工具。
什么叫线性接近,其实在二维平面内就是求变换率,也就是求一条接近的直线。
在三维空间内就是求一个平面去逼近一个多元函数。
至于怎么逼近,就是一系列的推到过程了。
反正我也不是很会,就记记结论:

还再补充两个比较有用的东东:
函数乘积:
f ( x ) = g ( x ) ∗ h ( x ) f(x)=g(x)*h(x) f(x)=g(x)∗h(x)
f ′ ( x ) = g ′ ( x ) ∗ h ( x ) + g ( x ) ∗ h ′ ( x ) f'(x)=g'(x)*h(x)+g(x)*h'(x) f′(x)=g′(x)∗h(x)+g(x)∗h′(x)
复合函数
设 y = f ( g ( x ) ) , u = g ( x ) 设y=f(g(x)),u=g(x) 设y=f(g(x)),u=g(x)
y ′ x ′ = f ′ ( u ) ∗ g ′ ( x ) \frac{y'}{x'}=f'(u)*g'(x) x′y′=f′(u)∗g′(x)
写成另外的形式就是:
f ( g ( x ) ) ′ = f ′ ( g ( x ) ) ∗ g ′ ( x ) f(g(x))'=f'(g(x))*g'(x) f(g(x))′=f′(g(x))∗g′(x)
导数的大概就怎么多了,其他的应该用不上。
积分
还记得那个神奇的问题吗?
求二次函数某段区间的面积。
这就是经典的积分形式。
比如求函数 f ( x ) = x 2 f(x)=x^2 f(x)=x2在 [ 1 , 2 ] [1,2] [1,2]区间内的面积。
那么可以写成这种形式:
∫ 1 2 f ( x ) d x \int_{1}^2f(x)dx ∫12f(x)dx
这个叫做 f ( x ) f(x) f(x)的积分。
牛顿-莱布尼兹公式(积分基本定理)
已知一个函数的积分:
∫ a b f ( x ) d x \int_a^bf(x)dx ∫abf(x)dx
那么把 f ( x ) f(x) f(x)看做是一个函数 F ( x ) F(x) F(x)的导函数,那么即可写成:
∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_a^bf(x)dx=F(b)-F(a) ∫abf(x)dx=F(b)−F(a)
证明?我也不会。记结论用就好了。
多项式对数函数(ln)
介绍
考虑一个奇怪的式子:
G ( x ) ≡ l n ( A ( x ) ) ( m o d x n ) G(x)\equiv ln(A(x))\ (mod\ x^n) G(x)≡ln(A(x)) (mod xn)
我们要求出 G ( x ) G(x) G(x)是多少。
(求 G ( x ) G(x) G(x)的意义目前我还不知道,但是求出这个之后和后面的exp组成连招可以加速很多东东。)
既然我们介绍到了导数,那么这个就可以用导数来求之。
过程
先把要用的两个柿子摆在这:
f ( x ) = b ∗ x a ; f ′ ( x ) = b ∗ a ∗ x a − 1 ; F ( x ) = b a + 1 ∗ x a + 1 f(x)=b*x^a;f'(x)=b*a*x^{a-1};F(x)=\frac{b}{a+1}*x^{a+1} f(x)=b∗xa;f′(x)=b∗a∗xa−1;F(x)=a+1b∗xa+1
设 F ( x ) = l n ( x ) F(x)=ln(x) F(x)=ln(x)
原式即可写成:
G ( x ) ≡ F ( A ( x ) ) ( m o d x n ) G(x)\equiv F(A(x))(mod\ x^n) G(x)≡F(A(x))(mod xn)
两边同时求导:
G ′ ( x ) ≡ F ′ ( A ( x ) ) A ′ ( x ) ( m o d x n ) G'(x)\equiv F'(A(x))A'(x)(mod\ x^n) G′(x)≡F′(A(x))A′(x)(mod xn)
G ′ ( x ) ≡ A ′ ( x ) A ( x ) ( m o d x n ) G'(x)\equiv \frac{A'(x)}{A(x)}(mod\ x^n) G′(x)≡A(x)A′(x)(mod xn)
那么 G ′ ( x ) G'(x) G′(x)就好做了,先把 A ( x ) A(x) A(x)求个导,然后求个逆,卷起来。
求出 G ′ ( x ) G'(x) G′(x)之后,还要把它积分回去,继续套上面的积分柿子即可。
当然,在做的时候可能要注意一下第一项。
代码
待填
学习资料:
百度百科(百度百科是真的详细)
同济大学——高等数学
https://www.cnblogs.com/knife-rose/p/12120373.html#1864488977
https://www.cnblogs.com/zwfymqz/p/10505188.html
https://www.cnblogs.com/zhangleo/p/11010374.html
前置芝士2:牛顿迭代
牛顿迭代
又称牛顿-拉弗森迭代。(可惜了这么多人想出的方法前面被套上了牛顿的大名)
牛顿迭代就是求一个函数的某个根的算法。(当然,求不同的根要从不同的角度来求)
条件:该函数可以二次求导。
原理其实很简单,就是先从某个点下手,求出在这个点时函数的切线。
然后求出切线后可以求出切线与x轴交点,求出交点后就继续从焦点位置做切线。
依次往复,即可迭代出一个根。
这里盗张图(https://www.matongxue.com/madocs/205.html)
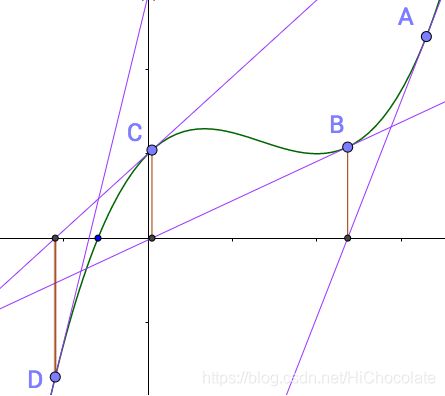
其中A是起点,迭代一次后得到B点,迭代两次后得到C点,迭代三次后得到D点……
然后我们发现若迭代的次数足够多,就可以无限接近于那个根。
写成柿子的形式就是:
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
其实就是解一下切线方程即可得到,或者说可以看做是泰勒展开取前两项。
至于正确性证明,我不会!还得看百度百科。
时间的话 O ( 能 过 ) O(能过) O(能过)
- 优点:简单,直观,好用。
- 缺点:有时候求出的根会很奇怪,而且求出的只是近似值。同时,条件比较苛刻。
一些不行的情况还是看其他大爷的博客把。
多项式的牛顿迭代
其实多项式的牛顿迭代还是和上面很相似的。
这个写出来还挺简单的。
想想牛顿迭代是干嘛的,就是做完一次操作之后,然后再推到下一次操作。
这是不是很像递推思想?如果多项式再把递推弄成倍增思想岂不更妙。
于是我们就考虑来弄弄。
设 G ( f ( x ) ) G(f(x)) G(f(x))表示当前的多项式函数为 G ( f ( x ) ) G(f(x)) G(f(x)),然后要求的多项式是 f ( x ) f(x) f(x)
一般式就写成:
G ( f ( x ) ) ≡ 0 ( m o d x n ) G(f(x))\equiv 0\ (mod\ x^n) G(f(x))≡0 (mod xn)
我们再设 f 0 ( x ) f0(x) f0(x)表示我们已经求出模 x ⌈ n 2 ⌉ x^{\lceil\frac n 2\rceil} x⌈2n⌉意义下的 f ( x ) f(x) f(x),现在要倍增上去求 f ( x ) f(x) f(x)
当然, n = 1 n=1 n=1时要特别求一下
那么考虑 G ( f ( x ) ) G(f(x)) G(f(x))在 f 0 ( x ) f0(x) f0(x)处的泰勒展开。
变成:
G ( f ( x ) ) = ∑ i = 0 I n f G ( i ) ( f 0 ( x ) ) ∗ ( f ( x ) − f 0 ( x ) ) i ∗ ( i ! ) − 1 G(f(x))=\sum_{i=0}^{Inf}G^{(i)}(f0(x))*(f(x)-f0(x))^i*(i!)^{-1} G(f(x))=i=0∑InfG(i)(f0(x))∗(f(x)−f0(x))i∗(i!)−1
然后我们发现,由于在 i > = 2 i>=2 i>=2的情况中,在模 2 n 2^n 2n意义下是 0 0 0,所以直接省略掉。
化简为:
G ( f ( x ) ) = G ( f 0 ( x ) ) + G ′ ( f 0 ( x ) ) ∗ ( f ( x ) − f 0 ( x ) ) G(f(x))=G(f0(x))+G'(f0(x))*(f(x)-f0(x)) G(f(x))=G(f0(x))+G′(f0(x))∗(f(x)−f0(x))
移项得:
f ( x ) = f 0 ( x ) − G ( f 0 ( x ) ) G ′ ( f 0 ( x ) ) f(x)=f0(x)-\frac{G(f0(x))}{G'(f0(x))} f(x)=f0(x)−G′(f0(x))G(f0(x))
就没啦。
应用?
先讲一个比较好玩的应用。
看到我们的多项式求逆。
看到那又臭又长的推导,十分不舒服。
学会牛顿迭代之后就3行:
考虑原式:
A ( x ) ∗ B ( x ) ≡ 1 ( m o d x n ) A(x)*B(x)\equiv 1(mod\ x^n) A(x)∗B(x)≡1(mod xn)
移项:
A ( x ) − 1 B ( x ) ≡ 0 ( m o d x n ) A(x)-\frac 1 {B(x)}\equiv 0(mod\ x^n) A(x)−B(x)1≡0(mod xn)
这就是牛顿迭代的形式。
那么设
G ( B ( x ) ) = A ( x ) − 1 B ( x ) G(B(x))=A(x)-\frac{1}{B(x)} G(B(x))=A(x)−B(x)1
迭代一下:
B ( x ) = B 0 ( x ) − G ( B 0 ( x ) ) G ′ ( B 0 ( x ) ) B(x)=B0(x)-\frac{G(B0(x))}{G'(B0(x))} B(x)=B0(x)−G′(B0(x))G(B0(x))
B ( x ) = B 0 ( x ) − A ( x ) − 1 B 0 ( x ) B 0 ( x ) − 2 B(x)=B0(x)-\frac{A(x)-\frac 1 {B0(x)}}{B0(x)^{-2}} B(x)=B0(x)−B0(x)−2A(x)−B0(x)1
化简得:
B ( x ) = 2 B 0 ( x ) − A B 0 ( x ) 2 B(x)=2B0(x)-AB0(x)^2 B(x)=2B0(x)−AB0(x)2
于是就得到求逆的基本递推式子啦~
多项式对数函数(exp)
介绍
考虑一个奇怪的式子:
B ( x ) ≡ e A ( x ) ( m o d x n ) B(x)\equiv e^{A(x)}\ (mod\ x^n) B(x)≡eA(x) (mod xn)
我们要求出 G ( x ) G(x) G(x)是多少。
求出来之后就可以直接套上ln打组合技了。
过程
由上式可知:
l n ( B ( x ) ) = A ( x ) ln(B(x))=A(x) ln(B(x))=A(x)
那么可以设 G ( B ( x ) ) G(B(x)) G(B(x))
G ( B ( x ) ) = l n ( B ( x ) ) − A ( x ) G(B(x))=ln(B(x))-A(x) G(B(x))=ln(B(x))−A(x)
牛顿迭代即可:
B ( x ) = B 0 ( x ) − G ( B 0 ( x ) ) G ′ ( B 0 ( x ) ) B(x)=B0(x)-\frac{G(B0(x))}{G'(B0(x))} B(x)=B0(x)−G′(B0(x))G(B0(x))
B ( x ) = B 0 ( x ) − l n ( B 0 ( x ) ) − A ( x ) B 0 ( x ) − 1 B(x)=B0(x)-\frac{ln(B0(x))-A(x)}{B0(x)^{-1}} B(x)=B0(x)−B0(x)−1ln(B0(x))−A(x)
B ( x ) = B 0 ( x ) ∗ ( 1 − l n ( B 0 ( x ) ) + A ( x ) ) B(x)=B0(x)*(1-ln(B0(x))+A(x)) B(x)=B0(x)∗(1−ln(B0(x))+A(x))
套一套就好了。
很easy!
代码
待填
多项式快速幂
介绍
这个是求这个东东的:
A ( x ) k ≡ B ( x ) ( m o d x n ) A(x)^k\equiv B(x)\ (mod\ x^n) A(x)k≡B(x) (mod xn)
过程
其实在学完上面两个东东之后,这个就是一眼秒的题了。
A ( x ) k = e k ∗ l n ( A ( x ) ) A(x)^k=e^{k*ln(A(x))} A(x)k=ek∗ln(A(x))
直接套板子吧~
代码
待填