python——k-means聚类算法
k-means聚类算法
k-means算法属于无监督学习的一种聚类算法,其目的为:在不知数据所属类别及类别数量的前提下,依据数据自身所暗含的特点对数据进行聚类。对于聚类过程中类别数量k的选取,需要一定的先验知识,也可根据“类内间距小,类间间距大“(一种聚类算法的理想情况)为目标进行实现。
需要用到sklearn库,scikit-learn是Python的一个开源机器学习模块,它建立在NumPy,SciPy和matplotlib模块之上能够为用户提供各种机器学习算法接口,可以让用户简单、高效地进行数据挖掘和数据分析。
语法解析
聚类算法:from sklearn.cluster import KMeans
def init(self, n_clusters=8, init=‘k-means++’, n_init=10, max_iter=300,tol=1e-4,precompute_distances=‘auto’,verbose=0, random_state=None, copy_x=True, n_jobs=1)
1. 输入参数:
-
n_clusters: 要分成的簇数也是要生成的质心数
类型 :整数型(int)
默认值:8 -
init: 初始化质心
类型 :可以是function 可以是array(random or ndarray)
默认值:采用k-means++(一种生成初始质心的算法)
kmeans++:种子点选取的第二种方法。
kmedoids(PAM,Partitioning Around Medoids)
能够解决kmeans对噪声敏感的问题。kmeans寻找种子点的时候计算该类中所有样本的平均值,如果该类中具有较为明显的离群点,会造成种子点与期望偏差过大。例如,A(1,1),B(2,2),C(3,3),D(1000,1000),显然D点会拉动种子点向其偏移。这样,在下一轮迭代时,将大量不该属于该类的样本点错误的划入该类。
为了解决这个问题,kmedoids方法采取新的种子点选取方式,1)只从样本点中选;2)选取标准能够提高聚类效果,例如上述的最小化J函数,或者自定义其他的代价函数。但是,kmedoids方法提高了聚类的复杂度。 -
n_init: 设置选择质心种子次数,默认为10次。返回质心最好的一次结果(好是指计算时长短)
类型 :整数型(int)
默认值:10
目的:每一次算法运行时开始的centroid seeds是随机生成的, 这样得到的结果也可能有好有坏. 所以要运行算法n_init次, 取其中最好的。 -
max_iter: 每次迭代的最大次数
类型 :整型(int)
默认值:300 -
tol: 容忍的最小误差,当误差小于tol就会退出迭代(算法中会依赖数据本身)
类型 :浮点型(float)
默认值:le-4(0.0001) -
precompute_distances: 这个参数会在空间和时间之间做权衡, 如果是True 会把整个距离矩阵都放到内存中,auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False时核心实现的方法是利用Cpython 来实现的
类型:布尔型(auto,True,False)
默认值:“auto” -
verbose: 是否输出详细信息
类型 :布尔型(True,False)
默认值:False -
random_state: 随机生成器的种子 ,和初始化中心有关
类型 :整型或numpy(RandomState, optional)
默认值:None -
copy_x: bool 在scikit-learn 很多接口中都会有这个参数的,就是是否对输入数据继续copy 操作,以便不修改用户的输入数据。这个要理解Python 的内存机制才会比较清楚。
类型 :布尔型(boolean, optional)
默认值:True -
n_jobs: 使用进程的数量,与电脑的CPU有关
类型 :整数型(int)
默认值:1
2.输出参数
-
label_: 每个样本对应的簇类别标签
r1 = pd.Series(model.labels_).value_counts() #统计各个类别的数目 -
cluster_centers_: 聚类中心
返回值:array, [n_clusters, n_features]
r2 = pd.DataFrame(model.cluster_centers_) #找出聚类中心
案例
#数据处理
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
from datetime import date,datetime
import numpy as np
from sklearn.cluster import KMeans #导入K均值聚类算法
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6 #rcParams设定好画布的大小
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
dir_path='E://DATA//'
outputfile = dir_path+'fenlei.csv'
data = pd.read_csv(dir_path+'full',sep='\x01',engine='python',header=None,names=[''], parse_dates=[''], infer_datetime_format=True,dtype={'':str,'':int}, encoding='utf-8')
#聚类开始
'''
算法过程:
1、从N个样本数据中随机选取K个对象作为初始的聚类质心。
2、分别计算每个样本到各个聚类中心的距离,将对象分配到距离最近的聚类中。
3、所有对象分配完成之后,重新计算K个聚类的质心。
4、与前一次的K个聚类中心比较,如果发生变化,重复过程2,否则转过程5.
5、当质心不再发生变化时,停止聚类过程,并输出聚类结果。
'''
k = 5 #需要进行的聚类类别数
iteration = 500 #聚类最大循环数
kmodel = KMeans(n_clusters = k, max_iter=iteration, n_jobs = 4) #n_jobs是并行数,一般等于CPU数较好
kmodel.fit(data) #训练模型
r1 = pd.Series(kmodel.labels_).value_counts() #统计各个类别的数目
r2 = pd.DataFrame(kmodel.cluster_centers_) #找出聚类中心
r = pd.concat([r2, r1], axis = 1) #横向连接(0是纵向),得到聚类中心对应的类别下的数目
r.columns = list(data.columns) + ['类别数目'] #重命名表头
#详细输出原始数据及其类别
r1 = pd.concat([data, pd.Series(kmodel.labels_, index = data.index)], axis = 1)
r1.columns = list(data.columns) + [u'聚类类别'] #重命名表头
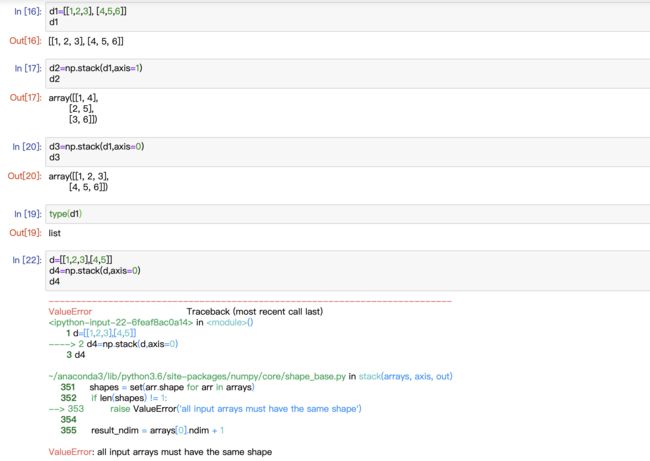
注1:Series是一个一维数组,Pandas 会默认用0到n-1作为series的index, 但也可以自己指定index( 可以把index理解为dict里面的key )
#聚类分析结果的降维可视化—TSNE
#效果并不好,无法区分各个类别,弃用
from sklearn.manifold import TSNE
tsne = TSNE()
tsne.fit_transform(data) #进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index = data4.index) #转换数据格式
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
#不同类别用不同颜色和样式绘图
d = tsne[r1[u'聚类类别'] == 0]
plt.plot(d[0], d[1], 'y.')
d = tsne[r1[u'聚类类别'] == 1]
plt.plot(d[0], d[1], 'go')
d = tsne[r1[u'聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*')
d = tsne[r1[u'聚类类别'] == 3]
plt.plot(d[0], d[1], 'c.')
d = tsne[r1[u'聚类类别'] == 4]
plt.plot(d[0], d[1], 'ro')
plt.show()
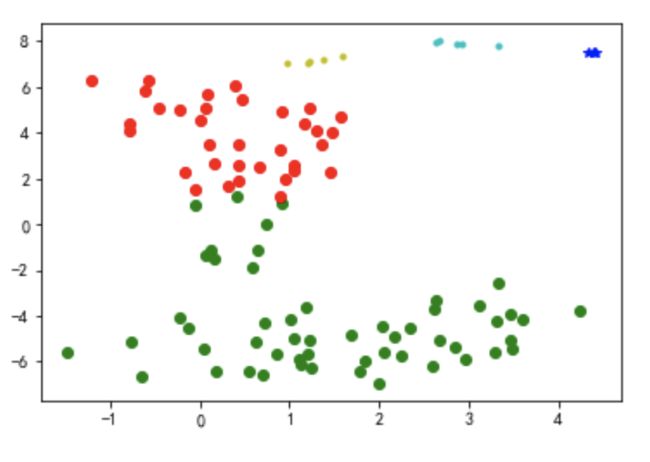
注2:tsne聚类结果可视化工具,tsne提供了一种有效的降维方式,让我们对高于2维数据的聚类结果以二维的方式展示出来
换一种展示方法:
行转列,做x轴为省份 y轴为和的聚类分布图
'''
行转列,做x轴为省份 y轴为均值的聚类分布图
'''
data1=r1.copy()
data1=data1.reset_index().set_index(['聚类类别','sku_no']).stack().reset_index()
p=data1['province'].drop_duplicates().reset_index().drop('index',axis=1).reset_index().set_index('province')
dic_p=p['index'].to_dict()
#聚类后的类折线图
data2=data1.copy()
data2['province']=data2['province'].map(dic_p)
plot_data=data2[['class','province','zb']].groupby(['class','province']).sum()
plot_data=plot_data.reset_index()
class_list=plot_data['class'].drop_duplicates().tolist()
for i,class_no in enumerate(class_list):
mask_class=plot_data['class']==class_no
plt.style.use('ggplot')
plt.plot(plot_data['province'].loc[mask_class],plot_data['zb'].loc[mask_class])
plt.xlabel('省份')
plt.show()
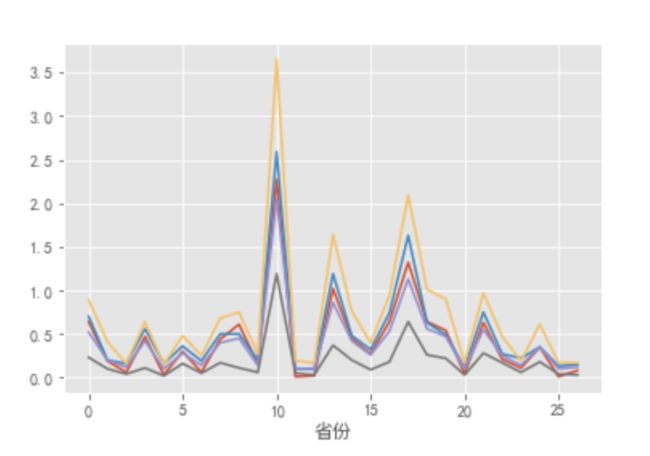
注3:stack,对list里面的每个元素(可能是个元组,或者是个numpy的数组)变成numpy的数组后,再对每个元素增加一维(至于维度加在哪里,是靠axis控制的),list每个元素必须形状是一样的
行转列,做x轴为省份 y轴为均值的聚类分布图
data3=data2[['class','province','sku_qty']].groupby(['class','province']).mean()
p_map=data9['province'].drop_duplicates().reset_index().set_index('province')
p_dict=p_map['index'].to_dict()
data3['province']=data3['province'].map(p_dict)
data3['class'].drop_duplicates()
class_list=data3['class'].drop_duplicates().tolist()
for i,class_no in enumerate(class_list):
mask_c=data9['class']==class_no
plt.xlabel('省份')
plt.scatter(data3['province'].loc[mask_c],data3['sku_qty'].loc[mask_c])
plt.show()